The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 29, No. 2, pp.3-8

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 30 Apr 2025

Received 16 Jan 2025 Revised 05 Mar 2025 Accepted 06 Mar 2025

DOI: https://doi.org/10.9726/kspse.2025.29.2.003

로프커터 감김사고 시 회전블레이드의 피로해석에 관한 연구

최혜진^*

; 서강현^*

; 이재웅^**^{, †}

*대학원생, 한국해양대학교 해사IT공학과
**부교수, 한국해양대학교 기관시스템공학부

Fatigue Analysis of Rotating Blade in Rope Cutters During Entanglement

Hyejin Choi^*

; Kanghyun Seo^*

; Jae-ung Lee^**^{, †}

*Graduate student, Department of Marine Information Technology, Korea Maritime & Ocean University.
**Associate Professor, Division of Marine System Engineering, Korea Maritime & Ocean University.

Correspondence to: ^†Jae-ung Lee : Associate Professor, Division of Marine System Engineering, Korea Maritime & Ocean University. E-mail : julee@kmou.ac.kr, Tel : 051-410-4662.

초록

선박 추진장치의 부유물 감김사고를 예방하기 위해 국내에서는 시저타입 로프커터가 널리 사용하고 있다. 하지만 대표적인 손상사례가 칼날 파단이라는 사실을 고려할 때, 회전블레이드의 구조적 건정성을 파악하는 연구는 부족하다. 이에 따라 본 연구는 회전블레이드가 로프에 감기어 회전하지 못하는 조건을 설정하여 블레이드의 피로해석을 실시하여, 회전체의 피로 취약부를 식별하고, 두께별 피로수명 변화를 살핀 후 취약부 파손을 예방하기 위한 최소 두께를 살펴보았다. 그 결과, 커터 허브와 블레이드가 만나는 부분이 취약부로 확인되며, 블레이드 두께가 13 mm에서 1 mm씩 증가함에 따라 안전계수가 약 6%씩 상승하고 14 mm에서 1 가까이 도달하였다. 취약부 수명은 13 mm에서 15 mm로 증가함에 따라 약 5배 이상 향상되어, 건전성 확보를 위한 최소 두께는 14 mm로 도출되었다.

Abstract

Scissor-type rope cutters are commonly used to prevent entanglement accidents in ship propulsion systems, yet little research exists on the structural integrity of their rotating blades. This study conducted a fatigue analysis simulating a scenario where the blade is tangled and unable to rotate. The analysis identified the fatigue-prone area, assessed the effect of blade thickness on fatigue life, and determined the minimum thickness to prevent fracture. Results showed that the junction between the cutter hub and blade is the most vulnerable part. Increasing the blade thickness from 13 mm to 14 mm improved the safety factor by about 6%, reaching nearly 1. Additionally, the fatigue life of the vulnerable part increased approximately fivefold as the thickness increased to 15 mm.

Keywords:

Scissor-type Ropte Cutters, Entanglement Accident, Rotating Blade, Faituge Analysis

키워드:

시저타입 로프커터, 감김사고, 회전블레이드, 피로해석

1. 서 론

어망과 로프는 어선에서 사용되는 기본 어업도구이며, 사용 후 바다에 폐기물로 버려지는 사례 때문에 소형 선박 추진기의 로프 감김사고의 주요 원인이다. 완전한 해양 폐기물 제거가 어려운 상황에서 감김사고를 효과적으로 방지하기 위해 시저타입 로프커터가 국내 연안선에 사용되는 추세다.¹⁾

시저타입 로프커터는 설치가 용이하며, 고정 블레이드와 회전블레이드로 구성되어 있다. 전자는 선체에 고정된 고정날이고, 후자는 추진축계에 설치된 회전날이며, 회전블레이드가 돌아가면서 고정 블레이드에 전단력을 주어 로프를 절단한다. 이것은 가위의 절단 방식과 흡사하며 축계의 토크를 이용하여 외부 이물질을 절단한다는 특징이 있다.

이와 관련하여 지속적인 학술활동으로 국산화를 위한 실증연구¹⁾와 절단장치 체결볼트의 안전수명연구²⁾ 및 로프절단장치가 축계에 미치는 영향³⁾에 관한 연구가 이루어졌다.

하지만 소형선박 추진기의 부유물 감김사고 수가 줄어들지 않고 있으며,⁴⁾ 국내에 수입되어 사용되고 있는 기존 로프커터의 대표적인 손상사례가 칼날 파단이라는 사실을 고려하였을 때,¹⁾ 회전 주기관으로부터 전달된 동적하중을 받고 있지만 회전블레이드가 로프에 감기어 회전하지 못하는 악조건에서 회전체가 받게 될 피로에 관한 연구는 부족한 실정이다.

본 연구는 재료의 내구성, 안전성, 수명을 평가할 수 있다는 피로해석의 장점에 착안하여⁵⁾ Ansys를 이용해 감김사고 발생 시 1) 커터의 회전체의 피로 취약부를 식별하고, 2) 커터 두께별 피로수명 변화를 살핀 후, 3) 취약부 파손을 예방하기 위한 최소 두께를 알아보고자 한다.

2. 연구내용

2.1 연구방법

본 연구에서 로프커터가 설치된 대상선박은 총 톤수 약 10톤의 소형선박으로 평균 1,300 rpm에서 약 730 HP의 출력을 내는 엔진을 탑재한 것으로 가정하였다.

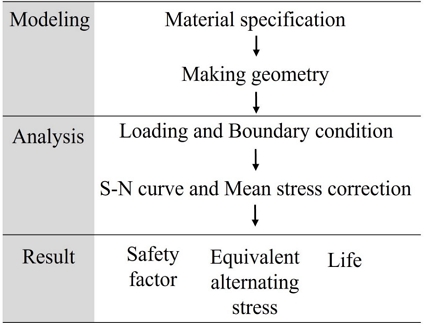
연구방법은 Fig. 1과 같다. 먼저 회전블레이드 캐드 모델링을 위해 재료의 물성치를 입력하고 형상을 만든 후, 피로해석을 위해 모델링에 하중 조건과 구속조건을 설정하였다. 피로에 대한 내구성과 안전성을 객관적인 수치로 계산하기 위해 기본이 되는 피로-수명선도와 평균응력보정법을 연구 목적에 맞게 선택하여 결과를 도출하였다.

Fig. 1

Simulation method

2.2 모델링

- 재료 물성치

로프커터의 재료는 높은 인장강도를 가진 STS630으로 선정하였다. STS630은 고강도 및 내식성을 가진 마르텐사이트계 석출경화 스테인리스강이다. 550~1,020℃에서 담금질 처리 후, 480℃에서 뜨임처리하는 열처리 과정을 거치기 때문에 변형 저항성과 피로 저항 등 기계적 성질이 커서 로프커터 재료로 사용되고 있다.¹⁾ Table 1은 본 재료의 물성치를 정리한 것이다.

Table 1

Material properties of STS630

- 로프커터 형상

Fig. 2는 대표적인 시저타입의 로프커터와 본 연구에서 모델링한 회전블레이드이다. 로프커터는 어망이 많은 해역에서 조업작업을 하는 어선에 많이 사용되기 때문에 총톤수가 10톤 미만의 소형어선에 적용된다고 가정하여 Table 2와 같이 회전날의 크기를 설계하였다.

Fig. 2

Scissor type rope cutter

Table 2

Specification of rope cutter

2.3 피로해석

- 하중과 구속조건

로프 감김사고 시 회전축과 회전블레이드 사이에 슬립이 발생할 수 있다. 슬립은 원래 함께 움직여야 할 두 표면 사이에서 발생하는 상대 운동을 의미한다. 이로 인해 블레이드가 로프에 감겨 자유롭게 회전하지 못하여 접촉면에서 발생한 슬립이 두 물체 사이의 응력 변동을 일으킬 수 있다는 뜻이다. 하지만 본 연구는 감김사고 시 블레이드 자체의 구조적 건전성을 확인하기 위하여 외력에 의한 회전체의 응력 발생과 피로해석을 목적으로 하기 때문에 접촉면에서 발생하는 슬립은 연구범위에서 제외하였다. 이에 따라 로프커터 모델링에 적용한 하중 및 구속 경계조건은 Fig. 3과 같이 설정하였다. 프로펠러축의 토크는 축과 연결되어 있는 로프커터의 붉은색 면을 통해 전달되기 때문에 해당 면에 약 4 kNm 토크값을 하중조건으로 설정하였으며, 구속조건은 칼날에 해당하는 보라색 면이 로프 감김으로 인해 움직이지 않는다고 가정하였다.

Fig. 3

Load and boundary conditions

- S-N 선도와 평균응력 보정

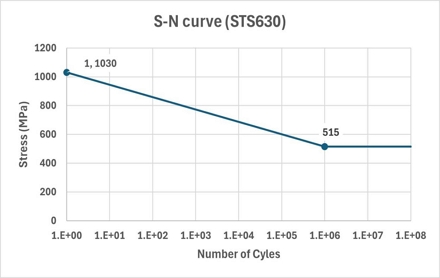
S-N선도는 일반적으로 피로 시험기를 통해 실험적으로 도출할 수 있지만, 실험 데이터가 없을 경우, 기존 연구에서 사용된 경험적 방법을 활용하여 추정할 수 있다.^6,7) 일반적으로 재료의 피로 한계는 항복강도의 50~60% 수준에서 설정되며,⁸⁾ 본 연구는 이를 기반으로 STS630의 S-N 선도를 추정하였다. Fig. 4에서는 1사이클에서 항복강도를 적용하였으며, 이는 초기 하중 적용 시 응력이 항복 수준에 도달함을 가정한 것이다. 또한 고사이클 피로 영역에서의 피로 한계를 설정하기 위해 10⁶사이클에서 항복강도의 50%인 515 MPa을 적용하였다.

Fig. 4

S-N curve of STS630

평균응력은 Gerber 방정식을 기준으로 보정되었다. 피로해석에서 평균응력을 보정하는 방법에는 Goodman, Morrow 및 Gerber 방정식 등이 있다. Gerber 방정식을 선택한 이유는 해당 방정식이 재료의 최대 응력과 평균 응력 간의 비선형 관계를 고려하기 때문에 해석 대상이 고응력 반복하중 및 연속적인 인장하중에 노출되는 경우, 더 현실적인 피로수명을 예측하는데 용이하기 때문이다. 로프커터의 칼날과 허브가 만나는 부분은 감김사고 시 인장 반복 하중에 노출된다. 이런 경우, Gerber 방정식이 적용되었을 때 피로수명을 더 정확하게 예측할 수 있을 것으로 예상되어 Gerber 방정식을 피로해석의 기준으로 정하였다.⁹⁾

3. 연구결과

2장에서 설정한 연구해석조건을 바탕으로 도출한 연구결과는 다음과 같다. 다만 커터 두께는 13 mm에서 15 mm까지 고려하였다. 이유는 일반 상용제품의 두께가 최소 10 mm이며, 14 mm부터 피로해석의 안전계수가 1에 가까워지기 때문이다.

- 두께별 피로 안전계수(Safety factor, S.F)

피로해석에서 안전계수는 식 (1)과 같이 계산되며, 이는 재료의 피로강도와 반복하중에 의해 발생한 응력의 비를 뜻한다.¹⁰⁾ 일반적으로 교번응력이 피로강보다 낮으면 피로파손이 발생하지 않는 것으로 간주할 수 있다.

S . F = M a t e r i a l ′ s f a t i g u e s t r e n g t h A p p l i e d s t r e s s

(1)

이에 따라 안전계수가 1보다 크면 피로파손으로부터 안정성을 확보했다고 이해할 수 있다.

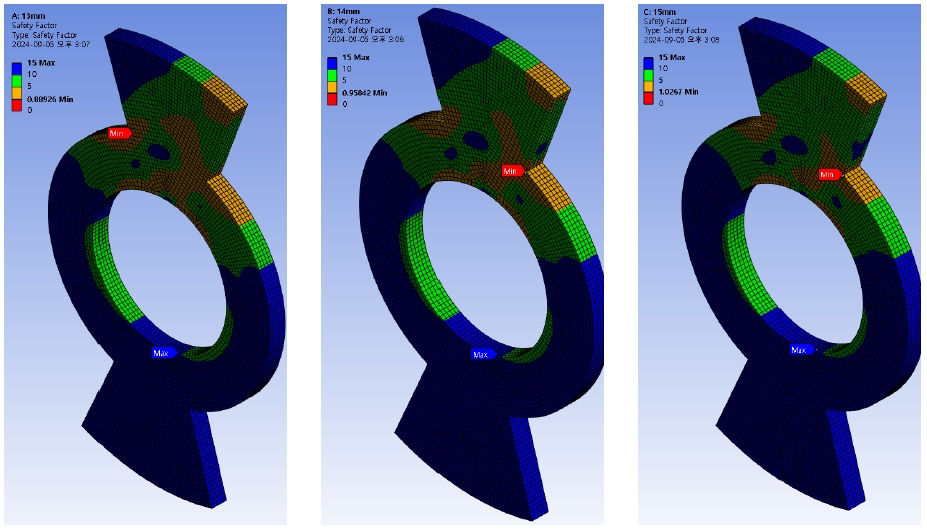
Table 3은 로프커터의 두께를 13 mm에서 15 mm까지 1 mm씩 늘렸을 때 계산된 안전계수의 최소 값을 정리한 것이며, Fig. 5는 각 두께별 안전계수 취약 부위를 나타낸다. 그림에서 회전블레이드의 두께가 13 mm인 경우, 반복응력에 취약한 곳은 로프 감김으로 회전이 구속된 블레이드 면의 반대쪽임을 알 수 있다.

Table 3

Safety factors according to thickness

Fig. 5

Safety factor result according to thickness

두께가 14 mm 이상이 되면, 응력 취약부는 로프가 감겨 구속된 칼날면과 커터 허브가 만나는 부분인 것으로 확인되었다. 두께가 두꺼워짐에 따라 취약부의 안전계수값이 약 6%씩 상승하며, 14 mm에서 처음으로 안전계수가 1 가까이 도달하여 피로 파손을 방지할 수 있는 최소 두께임을 확인하였다.

- 두께별 등가반복응력 최댓값

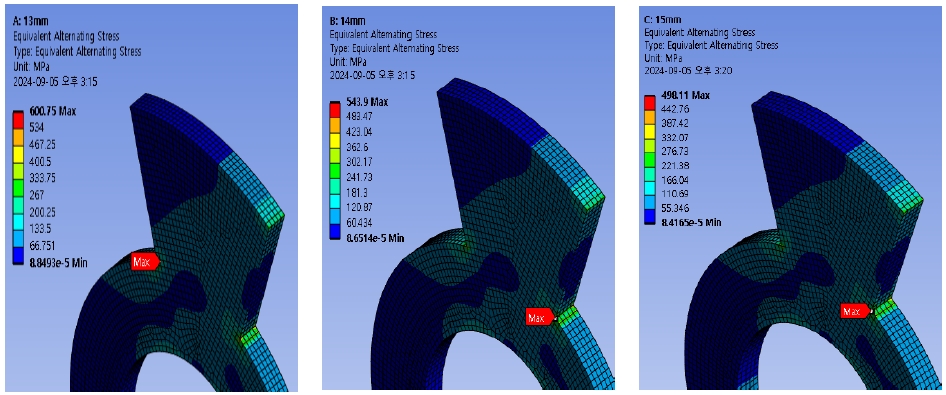
피로해석에서는 등가반복응력(Equivalent alternating stress)은 하중이 반복되거나 변할 때, 구조물에서 발생하는 반복적인 응력 크기를 나타낸다. 회전 블레이드에 로프 감김이 발생하여 블레이드가 회전하지 못하여 주어진 토크가 반복 하중으로 작용한다고 가정하면, Fig. 6에서 최대 교번응력이 발생한 지점과 그 크기를 알 수 있다.

Fig. 6

Equivalent alternating stress

모델링에서 동일한 구속조건과 하중조건을 적용했음에도 두께에 따라 등가 반복 응력이 부재의 기하하적 특성에 따라 분포가 다른 것을 확인하였다.

또한 앞서 설명한 안전계수 최솟값이 확인되었던 동일한 노드에서 최대 등가반복응력이 확인되었으며, 두께가 증가할수록 응력이 감소하는 것을 Table 4와 같이 확인할 수 있었다.

Table 4

Maximum equivalent alternating stress

- 두께별 취약부의 피로수명

피로수명은 구조물이 반복 하중에 노출될 때 얼마나 많은 하중 주기(cycle)를 견딜 수 있는지를 뜻한다. Table 5는 STS630의 S-N curve에 앞서 계산된 피로 취약부의 등가반복응력을 대입하여 계산된 피로수명 결과이다. 피로 취약부의 수명은 두께가 두꺼워짐에 따라 증가하는 경향을 보였으며, 14 mm 이상에서 충분한 수명을 확보할 수 있음을 확인하였다.

Table 5

Minimum life of vulnerable part

4. 결 론

본 연구는 국내 어선에서 가장 많이 사용되는 시저타입의 로프커터에서 로프감김 사고가 발생하여 회전블레이드가 회전하지 못하는 경우, 회전체에 발생하는 피로에 대해 분석하였다.

1) 두께가 1 3mm인 경우, 로프가 감겨 회전이 구속된 블레이드의 반대쪽 면이 응력에 취약한 부위로 나타났으나, 두께가 14 mm 이상으로 증가하면서부터 취약부는 커터 허브와 만나는 부분으로 이동하였다.

2) 두께가 증가할수록 안전계수와 피로수명이 향상되는 것을 확인하였다. 두께가 1 mm씩 증가할 때마다 안전계수는 약 6%씩 상승하였고, 두께가 14 mm 이상일 때 취약부의 안전계수는 1 가까이 도달하였다.

3) 또한 등가반복응력은 동일한 하중 조건에서 두께가 증가함에 따라 감소하는 경향을 보였고, 피로 취약부의 수명은 13 mm에서 15 mm로 증가함에 따라 약 5배 이상 향상되었다.

이에 따라 본 연구에서는 로프커터 회전블레이드의 구조적 안정성을 확보하기 위한 최소 두께를 14 mm로 도출하였다. 이는 두께 14 mm에서 안전계수가 1에 도달하고, 피로수명이 충분히 확보되며, 등가반복응력이 감소하는 경향이 확인되었기 때문이다.

추후 실제 손상사례를 확보하여 본 논문의 피로해석 연구방법과 손상 부위를 비교 분석하는 연구를 실시하여 피로해석 방법론을 보강해 나가고자 한다.

Acknowledgments

본 연구는 해양수산부와 해양수산과학기술진흥원 연구비 지원으로 수행된 ‘자율운항선박 기술개발사업(2020615)’의 연구 결과입니다.

Author contributions

H. J. Choi; Conceptualization, Investigation, Methodology, Visualization, Validation, Writing-original draft. K. H. Seo; Investigation, Resources, Visualization, Writing-review & editing. J. U. Lee; Funding acquisition, Investigation, Project adminstration, Supervision, Writing-review & editing.

References

Y. U. Sul, 2020, “An Empirical Study and Structural Analysis for localization of Ship’s Rope cutter”, Master thesis, National Korea Maritime and Ocean University.
W. J. Lee, J. H. Kim, S. H. Jang, K. W. Lee, B. Y. Kim, W. K. Lee and J. H. Choi, 2018, “A Study on Safety and Performance of Rope Cutter for Ship's Propeller”, Journal of the Korean Society of Marine Environment & Safety, 24(4), 475-481. [https://doi.org/10.7837/kosomes.2018.24.4.475]
W. S. Kwon, Q. D. Vuong, J. H. Choi, J. U. Lee, J. W. Lee, S. H. Yoon and W. J. Lee, 2022, “Study on the propeller rope cutter concerning transient torsional vibration due to cutting action”, Applied Sciences, 12(3), 1628. [https://doi.org/10.3390/app12031628]
https://www.kmst.go.kr/web/stcAnnualReport.do?menuIdx=126, (access:24.10.14).
R. I. Stephens, A. Fatemi, R. R. Stephens and H. O. Fuchs, 2000, Metal fatigue in engineering, John Wiley & Sons.
https://www.instron.com/ko-kr/resources/test-types/dynamic-test, (access:24.09.30).
H. J. Choi, K. H. Seo, Y. M. Kim, J. W. Lee and J. U. Lee, 2023, “Torsional Stress and Fatigue Life Analysis on The Propulsion Shaft During Crash Astern”, Journal of Power System Engineering, 27(3), 20-27. [https://doi.org/10.9726/kspse.2023.27.3.020]
https://www.banditong.com/ko-kr/s-technology/cae-technote/reference_fatigue_analysis, (access:24.09.30).
C. C. Chu, 2000, Comparison of mean stress correction methods for fatigue life prediction (No. 2000-01-0778), SAE Technical Paper.
N. E. Dowling, S. L. Kampe and M. V. Kral, 2013, Mechanical behavior of materials: engineering methods for deformation, fracture, and fatigue, Pearson.