유체 어드미턴스의 전달을 이용한 유압관로계의 주파수 응답 해석
초록
유체 어드미턴스의 전달을 이용하여 유압관로, 어큐뮬레이터, 교축요소, 저장용량요소 등으로 구성된 유압관로계의 주파수 응답을 구하는 새로운 방법을 개발하였다. 이 방법은 출구의 경계조건으로부터 마지막 절점의 유체 어드미턴스를 먼저 구한 후, 출구에서 입구 방향으로 각 절점의 유체 어드미턴스를 차례로 계산한다. 그리고 유압관로의 입구에서 유체 어드미턴스와 경계조건을 이용하여 압력을 구한 후, 압력전달계수를 이용해 유압관로계의 입구에서 출구 방향으로 각 절점의 압력을 차례로 계산한다. 절점의 유량은 절점의 압력과 유체 어드미턴스의 곱으로부터 구할 수 있다. 개발된 방법을 토대로 전산 프로그램을 만들고 3가지 계산모델을 선정하여 수치 계산을 행한 후, 동일 모델에 대한 선행 연구자의 실험, 해석 그리고 전산 프로그램 결과와의 비교를 통해 개발된 방법의 신뢰성을 확인하였다.
Abstract
A new method for obtaining frequency response of oil hydraulic pipeline system composed of oil hydraulic pipelines, accumulators, throttling elements, and storage capacitor elements etc. was developed using the transfer of fluid admittance. This method calculates the fluid admittance of each node from the outlet to the inlet in turn, after first obtaining the fluid admittance of the last node from the boundary condition of the outlet. Moreover, the pressure at each node is calculated from the inlet to the outlet of the system in turn using the pressure transfer coefficient, after obtaining the pressure of the first node using the fluid admittance of the first node and boundary condition of the inlet. The flow rate of a node can be obtained from the product of the pressure and the fluid admittance of the node. After numerical calculations are performed on three computational models using a computer program based on this method, the reliability of this method is confirmed through comparisons with results of experiment, analysis, and computer program of prior researchers on the same models.
Keywords:
Oil Hydraulic Pipeline System, Frequency Responses, Fluid Admittance, Transfer Admittance Method, Transfer Matrix Method키워드:
유압관로계, 주파수 응답, 유체 어드미턴스, 전달 어드미턴스법, 전달 매트릭스법1. 서 론
유압 작동유를 사용하여 압력과 유량을 전달하는 유압 시스템은 건설, 선박, 항공, 로봇 등 다양한 분야에서 현재 널리 사용되고 있다. 유압 시스템은 유압 펌프, 어큐뮬레이터(accumulator), 교축기구(밸브) 등 다양한 요소로 구성되는데, 이들은 유압 관로를 통해 서로 연결되며 관로 내부 작동유의 유동 상태에 따라 유압 시스템의 응답에 많은 영향을 준다. 따라서 다양한 요소로 구성된 유압관로계의 동특성을 해석하는 것은 공학적으로 가치 있는 일이다.
유압관로계의 유동을 해석하는 방법으로는 주파수 응답으로 해석하는 방법과 시간 응답으로 해석하는 방법이 있다. 이 중 주파수 응답은 넓은 주파수 영역에서 유압관로계의 전체적인 동특성을 파악하는데 도움을 주며, 널리 이용되는 방법으로서 전달 매트릭스법(transfer matrix method)이 있다.
D’Souza와 Oldenburger는 탄성 관로의 동특성을 해석하기 위해 전달 매트릭스를 구한 후 주파수 응답 해석 결과와 실험 결과가 잘 일치함을 확인하였다.1) Nakano와 Yoshimoto는 점탄성 관로의 주파수 응답을 계산할 수 있는 전달 매트릭스를 구하여 동특성을 해석하였다.2) Muto 등은 테이퍼(taper)를 갖는 유압관로계에 대한 전달 매트릭스를 유도하고 그것을 토대로 복합관을 포함한 각종 테이퍼 관로계의 동특성을 해석하였다.3)
Lee 등은 전달 매트릭스법을 활용하여 어큐뮬레이터, 고압호스와 같은 비선형 특성이 현저한 관로 요소를 포함한 관로망의 압력 맥동 해석법을 개발하였다.4-7) Mo 등은 동력전달 관로계 내의 맥동주파수 분석을 통해 유체전파 소음의 발생 메커니즘을 해석하였다.8) Lee와 Oh는 자동차의 유압식 조향시스템에 사용되는 튜너 내장 조향 호스의 모델링과 해석 그리고 실험에 대한 연구를 수행하였다.9) Kim은 유압관로를 분포정수계로 모델링하여 전달행렬과 경계조건을 이용하여 주파수 응답을 구하고 MATLAB을 유리함수 형태의 전달함수로 근사화하여 시간영역에서 유압관로의 과도응답 특성을 조사하였다.10)
과거에 저자들은 강성계수의 전달을 이용하여 응력해석, 자유진동해석, 강제진동해석, 그리고 과도응답해석 등 구조물의 정적·동적 해석을 효과적으로 수행하는 방법을 개발하여 보, 판, 셸 등 다양한 구조물에 적용하고, 그 신뢰성 및 유효성을 제안한 바 있다. 그러나 이러한 연구들은 모두 고체 구조물에 국한되었다.11,12)
이 연구에서 저자들은 해석대상을 과거의 고체 구조물에서 벗어나 유체의 유동 해석 분야에 적용할 수 있는 새로운 해석 방법에 대해 연구하게 되었고, 그 결과 유압관로계에서 유체 어드미턴스의 전달을 이용하여 유압관로계의 주파수 응답을 구하는 방법을 개발하였다(이하에서 이 방법을 전달 어드미턴스법(transfer admittance method)이라 부른다). 이 논문에서는 유압관로, 어큐뮬레이터, 교축요소, 저장용량요소 등으로 구성된 유압관로계를 대상으로 전달 어드미턴스법으로 주파수 응답을 구하는 과정을 자세히 기술한다.
2. 전달 어드미턴스법
2.1 모델링
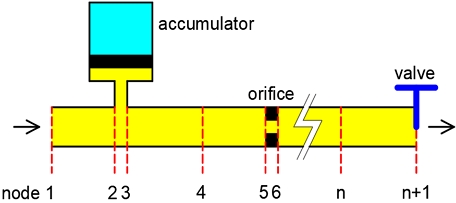
Fig. 1은 이 연구의 대상인 유압관로계의 한 예로써, 금속제 관로, 관로 상의 어큐뮬레이터, 오리피스, 밸브 등으로 구성된 해석모델이다.
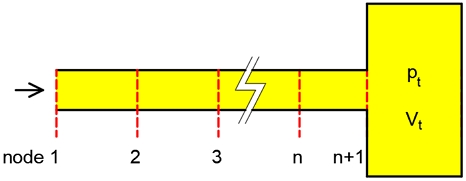
이 연구에서 요소와 요소 사이의 결합점 그리고 유압관로계의 입구와 출구를 모두 절점(node)이라 부른다. 해석대상 시스템이 총 n개의 요소로 구성된다면 시스템은 총 n+1개의 절점을 가지게 되고, 입구로부터 순차적으로 각 절점을 절점 1, 절점 2, 절점 3 ⋯이라 하고, 출구에 해당하는 마지막 절점은 절점 n+1이 된다.
시스템의 경계조건은 절점 1과 절점 n+1에서 지정되는데, 관로가 완전히 개방된 경우, 관로가 완전히 폐쇄된 경우, 관로 끝에 탱크와 같은 저장용량요소가 존재하거나, 밸브와 같은 교축요소가 존재하는 경우 등이 가능하다.
2.2 유체 어드미턴스의 정의 및 전달
유압관로계의 해석적 분할점인 절점에서, 유량(q)과 압력(p)을 라플라스 변환한, 와 사이의 관계를 아래 식과 같이 유체 어드미턴스(fluid admittance) 를 이용하여 정의한다.
| (1) |
이 연구에서 하첨자는 해당 절점 또는 해당 요소를 의미하며, 식 (1)의 는 절점 i의 유체 어드미턴스이다.
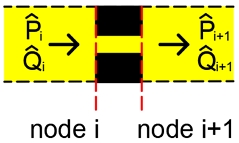
해석모델(Fig. 1)에서 임의의 i번째 요소가 Fig. 2와 같은 금속제 관로요소라면, 관로요소 좌우측 절점의 압력과 유량 사이의 관계를 식 (2)와 같이 전달 매트릭스로 표시할 수 있다.
| (2) |
유속이 음속보다 낮고 비정상 층류 유동을 하는 관로요소를 분포정수계(distributed parameter system)로 모델링하면 식 (2)의 전달행렬은 다음 식과 같이 나타낼 수 있다.4-6,10)
| (3) |
여기서,
| (4) |
| (5) |
이다. 식 (4)와 (5)에서 l은 관로의 길이, r은 관로내 반경, c는 관로 내 음속, ρ는 유체의 밀도, ν는 유체의 동점성계수, j는 허수단위(), s는 라플라스 연산자, J0 및 J1은 제1종 0차 및 1차의 베셀(Bessel) 함수이다.
한편, 관로요소를 집중정수계(lumped parameter system)로 모델링한다면 식 (2)의 전달행렬은 식 (6)과 같다.13)
| (6) |
여기서, R은 유체 저항(fluid resistance), C는 유체 용량(fluid capacitance), L은 유체 인덕턴스(fluid inductance)로서 다음 식과 같다.
| (7) |
| (8) |
| (9) |
그리고 식 (9)의 K는 체적탄성계수(bulk modulus)이다.
식 (1)과 식 (2)로부터 i번째 관로요소 양측 압력 사이의 관계 식을 아래와 같이 나타낼 수 있다.
| (10) |
여기서, 는 식 (11)과 같고, 관로요소의 압력전달계수(pressure transfer coefficient)라 정의한다.
| (11) |
식 (1)과 식 (2) 그리고 식 (10)과 식 (11)로부터 다음 식을 유도할 수 있다.
| (12) |
상기 식은 관로요소를 대상으로 요소 우측 절점의 유체 어드미턴스()를 가지고 요소 좌측 절점의 유체 어드미턴스()를 구하는 전달식이다.
해석모델(Fig. 1)에서 임의의 i번째 요소가 오리피스 또는 밸브와 같은 교축요소(throttling element)라면, 이 요소 좌우측 절점의 압력과 유량 사이의 관계를 식 (13)과 같이 표시할 수 있다.5,6)
| (13) |
관로 내의 흐름이 층류인 경우 다음과 같다.
| (14) |
이고, 및 은 동작점에서 절점 i 및 절점 i+1의 압력이고, 는 동작점에서 절점 i의 유량이다. 식 (1)과 식 (13)으로부터 i번째 교축요소 양측 압력 사이의 관계를 아래 식 (15)와 같이 나타낼 수 있다.
| (15) |
여기서, 는 식 (16)과 같고, 교축요소의 압력전달계수라 정의한다.
| (16) |
식 (1)과 식 (13) 그리고 식 (15)와 식 (16)으로부터 다음 식을 유도할 수 있다.
| (17) |
상기 식은 밸브 또는 오리피스와 같은 교축요소를 대상으로 요소 우측 절점의 유체 어드미턴스()를 가지고 요소 좌측 절점의 유체 어드미턴스()를 구하는 전달식이다.
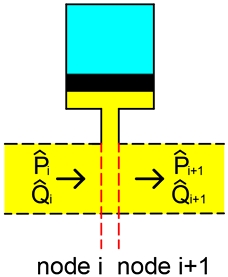
해석모델(Fig. 1)에서 임의의 i번째 요소가 관로 상에 부착된 벨로즈식 또는 피스톤식 어큐뮬레이터(Fig. 4)라면 연결된 관로 좌우측 절점의 압력과 유량 사이의 관계를 식 (18)과 같이 표시할 수 있다.5,7)
| (18) |
어큐뮬레이터가 피스톤식인 경우 다음과 같다.
| (19) |
여기서, , , , fp는 피스톤의 마찰계수, Ap는 피스톤의 단면적, , ln은 어큐뮬레이터 접속 관로의 길이, An은 어큐뮬레이터 접속 관로의 단면적, , mo는 어큐뮬레이터 내에서 피스톤의 운동에 따라 움직이는 기름의 질량, mp는 피스톤의 질량, mn는 어큐뮬레이터와 관로 사이 연결 관로부의 기름의 질량, ρ와 ν는 유압 작동유의 밀도와 동점도, βg와 Vg는 어큐뮬레이터 내 질소 가스의 압축율과 체적이다.
어큐뮬레이터가 벨로즈식인 경우에는 식 (19)의 값은 참고문헌에 자세히 기술되어 있다.4,5,7)
식 (1)과 식 (18)로부터 i번째 요소인 어큐뮬레이터 양측 압력 사이의 관계를 아래 식과 같이 나타낼 수 있다.
| (20) |
여기서, 는 식 (21)과 같고, 어큐뮬레이터의 압력전달계수라 정의한다.
| (21) |
식 (1)과 식 (18) 그리고 식 (20)과 식 (21)로부터 다음 식을 유도할 수 있다.
| (22) |
상기 식은 피스톤식 또는 밸로즈식 어큐뮬레이터가 부착된 관로 상에서 관로 우측 절점의 유체 어드미턴스()를 가지고 관로 좌측 절점의 유체 어드미턴스()를 구하는 전달식이다.
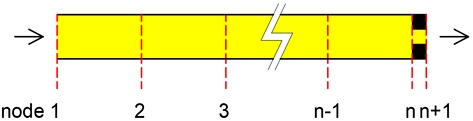
2.3 관로 출구의 유체 어드미턴스
유압관로계의 출구는 완전히 폐쇄된 경우, 완전히 개방된 경우, 관로 끝에 탱크와 같은 저장용량요소가 존재하거나 밸브와 같은 교축요소가 존재하는 경우 등 다양한 경계조건이 존재할 수 있다. 전달 어드미턴스법에서는 유압관로 출구의 경계조건에 따라 해석모델의 마지막 절점인 절점 n+1의 유체 어드미턴스()를 먼저 구한 후 전달식을 이용하여 나머지 절점의 유체 어드미턴스를 계산한다.
절점 n+1에서 식 (1)을 변형하면 다음 식 (23)과 같다.
| (23) |
유압관로의 출구가 폐쇄된 경우, 유량 은 0이 되므로, 유체 어드미턴스 은 0이 된다.
관로 출구가 아무런 저항 없이 대기압을 받는 외부로 방출된 경우, 절점 n+1의 게이지 압력(pn+1)은 0이 되므로 도 0이 되어 식 (23)으로부터 은 ∞가 된다. 그리고 출구가 정압 탱크에 연결된 경우에도 절점 n+1의 압력은 일정하여 변화가 없으므로 은 0이 되어 유체 어드미턴스 은 ∞가 된다. 참고로, 이 경우에는 전산 프로그램 실행 시에 ∞에 해당하는 아주 큰 값인 1020을 의 변수 값에 대입하여 계산한다.
출구가 오리피스와 같은 교축요소를 통해 외부로 방출된다면, 해석모델의 마지막 요소(n번째 요소)가 교축요소가 된다. 이 경우는 이 되므로, 식 (13)으로부터 이 되므로, 어드미턴스 이 된다. 이것은 식 (17)의 에 ∞를 대입한 것과 동일한 결과가 된다.
관로 출구(절점 n+1)에 일정한 체적(Vt)을 갖는 저장용량요소가 연결된 경우, 저장용량요소의 탄성 효과를 무시하고, 관로 출구의 압력(pn+1)과 탱크 내부압력(pt)이 같다고 가정하면 출구의 유량 qn+1 (t)은 다음 식이 된다.
| (24) |
상기 식을 라플라스 변환하여 다음 식을 구할 수 있다.10)
| (25) |
따라서 관로 출구에 일정한 체적(Vt)을 갖는 저장용량요소가 연결된 경우, 유체 어드미턴스 은 sVt/K가 된다.
2.4 유압관로계의 주파수 응답 해석
2.3절에서 기술한 방법으로 유압관로 출구의 경계조건을 고려하여 절점 n+1의 유체 어드미턴스를 먼저 구한다. 그리고 2.2절에서 요소별로 정식화한 전달식을 이용하여 유압관로계의 출구에서 입구 쪽으로 거슬러 올라가면서 각 절점의 유체 어드미턴스를 계산한다.
유압관로의 입구인 절점 1에서 압력()을 안다면 식 (1)로부터 절점 1의 유량()을 구할 수 있다. 또는 절점 1에서 유량()을 안다면 압력()을 구할 수 있다.
나머지 절점의 압력은 유체 어드미턴스의 전달과정에서 계산하고 저장해 둔 압력전달계수 를 이용()해 입구에서 출구 방향으로 순차적으로 각 절점의 압력을 쉽고 빠르게 계산할 수 있다. 그리고 절점의 유량은 식 (1)을 통해 해당 절점의 어드미턴스와 압력을 곱하여 구할 수 있다.
진동수별로 모든 상태량(압력과 유량)을 계산한 후, 출력 상태량을 입력 상태량으로 나누면 전달함수를 구할 수 있다. 상기 과정에서 절점 1의 압력과 유량을 모두 모른다 할지라도 둘 중 하나의 값을 1로 두고 상기 과정을 진행하면 전달함수를 쉽게 구할 수 있다.
3. 계산 결과 및 고찰
3.1 계산모델 1
전달어드미턴스법(TAM)의 신뢰성을 확인하기 위해 도입한 첫 번째 계산모델은 Fig. 5와 같이 입구에 유압유가 공급되고, 출구는 오리피스를 통해 대기로 방출되는 모델로서, D’Souza와 Oldenburger에 의해 제시된 바 있다.1) 이 모델에서 관로는 길이 12.27 m(= 40.25 ft), 내경 12.57 mm(= 0.495 in), 재료는 스테인리스강이다. 작동유는 밀도 857.0 kg/m(=1.663 lb·s2/ft4), 동점도 18.30×10-6 m2/s(= 197×10-6 ft2/s)인 Mil-O-5606이고, 관로 내의 음속은 1295 m/s(= 4250 ft/s)이다.
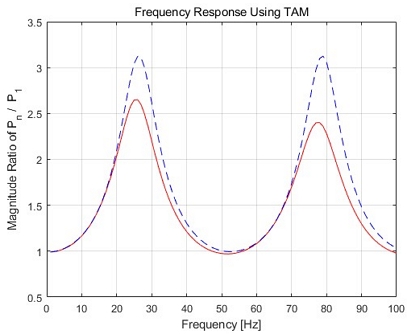
Fig. 6은 연구에서 제안한 전달어드미턴스법으로 1 Hz에서 100 Hz 사이의 주파수 영역에서 계산모델 1의 입구 압력 진폭()에 대한 오리피스 직전의 출구 압력 진폭()의 비를 계산한 결과이다. Fig. 6에서 붉은 실선은 전달어드미턴스법으로 유압관로를 1개의 분포정수계로 모델링하여 계산한 결과이며 앞선 D’Souza의 실험 및 계산 결과와 아주 잘 일치하였다.1) 그리고 Fig. 6에서 푸른 파선은 전달어드미턴스법으로 관로를 100개의 집중정수계로 모델링하여 계산한 결과이다.13) 분포정수계의 결과와 비교해 보면 공진점의 위치는 유사하지만 집중정수계로 계산한 진폭비는 분포정수계보다 상대적으로 크며, 주파수가 커질수록 그 차이가 더 증가함을 알 수 있었다.
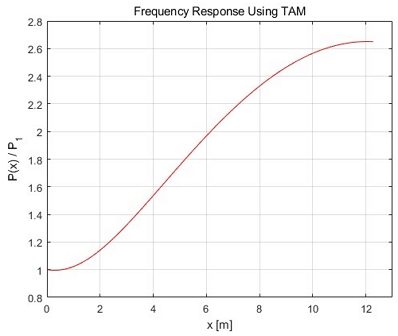
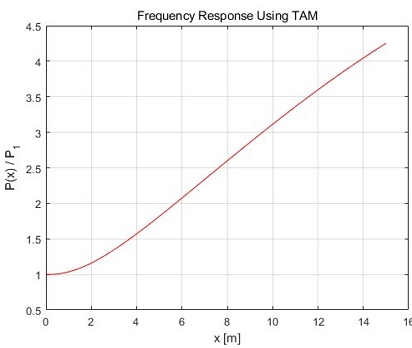
Fig. 6으로부터 계산모델 1의 1차 공진점이 26 Hz 부근임을 알 수 있었다. Fig. 7은 계산모델 1의 1차 공진점 부근인 26 Hz에서 입구 압력()에 대한 관로 위치별 압력()의 전달함수를 계산한 결과이다. 입구에서 출구로 갈수록 압력이 증가하고 있고, 출구에서 입력 압력의 2.5배를 초과하며 관로 출구에서 가장 크다는 것을 알 수 있었다.
3.2 계산모델 2
전달어드미턴스법의 신뢰성을 확인하기 위해 도입한 2번째 계산모델은 Fig. 8과 같이 유압관로 출구에 저장용량요소가 있는 경우로서, Kim에 의해 제시된 바 있다.10) 이 모델의 작동유는 밀도 860 kg/m3, 동점도 46.2×10-6 m2/s, 체적탄성계수 1.5 GPa이고, 관의 길이는 15 m, 내경은 10 mm이다. 그리고 저장용량요소의 체적은 1.178×10-3 m3이다.
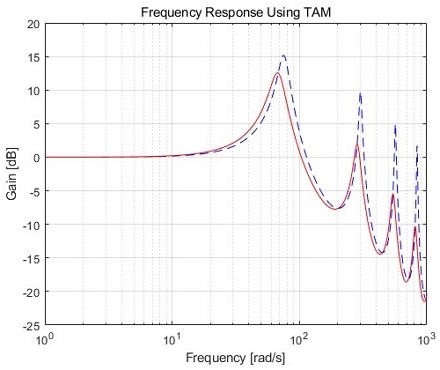
Fig. 9는 전달어드미턴스법으로 계산모델 2의 입구 압력 진폭()에 대한 출구 압력 진폭()의 전달함수를 1,000 rad/s 이하의 주파수 영역 범위 안에서 계산한 결과이다.
Fig. 9의 붉은 실선은 유압관로를 1개의 분포정수계로 모델링하여 계산한 결과이며, Kim의 결과와 아주 잘 일치하였다.10) Fig. 9에서 푸른 파선은 전달 어드미턴스법으로 관로를 100개의 집중정수계로 모델링하여 계산한 결과이다. 분포정수계의 결과와 비교해 보면 집중정수계로 모델링한 것도 유사한 경향을 보여 주지만 진폭이 상대적으로 크고 공진점의 위치가 약간씩 차이가 있었다.
Fig. 9로부터 계산모델 2의 1차 공진점이 67 rad/s 부근임을 알 수 있었다. Fig. 10은 계산모델 2의 1차 공진점 부근인 67 rad/s에서 입구 압력()에 대한 관로 위치별 압력()의 전달함수를 계산한 결과이다. 입구에서 출구로 갈수록 압력이 증가하고 있으며, 출구에서 입력 압력의 4배를 초과하며 관로 출구에서 가장 크다는 것을 알 수 있었다.
3.3 계산모델 3
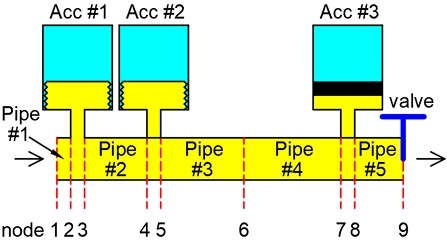
3번째 계산모델은 Fig. 11과 같이 분포정수계로 모델링한 5개의 관로요소와 관로 상에 위치한 3개의 어큐뮬레이터로 구성된 모델이다.
관로요소의 길이는 입구에서 차례로 20 mm, 210 mm, 690 mm, 1600 mm, 200 mm이고, 관로 내경은 모두 8 mm이다. 관로 내의 음속은 1300 m/s이고, 작동유는 밀도 869 kg/m3, 동점도 40×10-6 m2/s이다.
입구로부터 첫 번째 어큐뮬레이터는 관로 내 압력이 0인 상태에서 초기 체적이 8.5 cm3, 가스 충전 압력이 60 bar인 벨로즈식 어큐뮬레이터이다. 두 번째 어큐뮬레이터는 초기 체적이 200 cm3, 가스 충전 압력이 70 bar인 벨로즈식 어큐뮬레이터이다. 세 번째 어큐뮬레이터는 초기 체적이 380 cm3, 가스 충전 압력이 64 bar인 피스톤식 어큐뮬레이터이다. 어큐뮬레이터 내의 가스는 질소로서 비열비는 1.65이다.
관로 입구는 유압 펌프에 연결되는데, 이 펌프는 사판식 피스톤 펌프로서 9개의 피스톤을 가지며, 펌프 직후인 관로 입구에서 평균 게이지 압력이 100 bar, 펌프의 체적효율은 0.91, 행정용적이 1.270×10-5 m3, 유량 맥동 진폭은 각진동수(ω)의 함수로서 1.06×10-6+1.06×10-8ω이다.
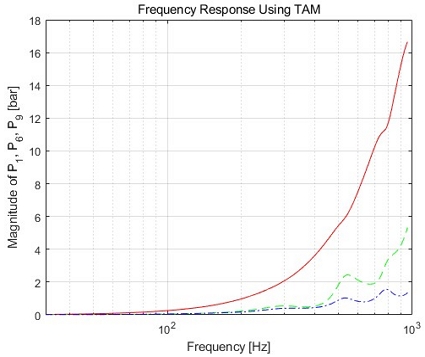
Fig. 12는 전달어드미턴스법으로 200 rad/s에서 6,000 rad/s의 주파수 영역에서 계산모델 3의 절점 1, 절점 6, 절점 9의 압력 진폭을 주파수별로 계산한 결과이다. 여기서 붉은 실선은 절점 1, 초록 파선은 절점 6, 푸른 일점쇄선은 절점 9의 압력 진폭을 의미한다. 어큐뮬레이터의 효과로 입구에서 멀어질수록 압력이 감소함을 알 수 있었다. 그리고 Lee 등이 전달 매트릭스법을 기반으로 개발한 단일 관로 해석 프로그램(PABM)의 결과와도 잘 일치하였다.4)
4. 결 론
저자들은 유압관로, 어큐뮬레이터, 교축요소, 저장용량요소 등 다수의 요소로 구성된 유압관로계를 대상으로 유체 어드미턴스의 전달을 이용하여 유압관로계의 주파수 응답을 해석하는 새로운 방법을 개발하였다.
이 방법을 간략히 소개하면 다음과 같다. 유압관로계의 각 절점에서 유량과 압력의 관계로부터 유체 어드미턴스를 정의한다. 그리고 출구의 경계조건으로부터 마지막 절점의 유체 어드미턴스를 먼저 구하고, 출구에서 입구 방향으로 전달하듯이 각 절점의 유체 어드미턴스를 순차적으로 구한다. 유압관로의 입구인 절점 1에서 압력과 유체 어드미턴스의 곱으로부터 절점 1의 유량을 계산할 수 있고, 또는 절점 1의 유량을 유체 어드미턴스로 나누어 절점 1의 압력을 구할 수 있다. 그리고 유압관로의 입구에서 출구 방향으로 각 절점의 압력을 압력전달계수를 이용하여 순차적으로 계산한다. 각 절점의 유량은 그 절점의 압력과 유체 어드미턴스의 곱으로부터 구할 수 있다.
이 연구에서 개발한 방법을 토대로 전산 프로그램을 만들고 3가지 계산모델을 선정하여 수치 계산을 행한 후, 동일 모델에 대한 선행 연구자의 실험, 해석 그리고 전산 프로그램 결과와의 비교를 통해 이 연구에서 제안된 방법의 신뢰성을 확인하였다.
이 연구를 통해 전달 어드미턴스법이 기존의 전달 매트릭스법에 비해 해석 알고리즘이 단순하고 전산화하기 용이하다는 것을 알 수 있었다. 앞으로는 분지계 등을 갖는 복잡한 유압관로계의 주파수 응답 해석 및 과도응답 해석에도 적용할 수 있도록 전달 어드미턴스법의 활용성을 높이는 연구를 수행할 계획이다.
Author contributions
K. Y. Yang; Conceptualization, Validation, Writing-review & editing. M. S. Choi; Investigation, Methodology, Software, Writing-original draft.
References
-
A. F. D’Souza and R. Oldenburger, 1964, “Dynamic Response of Fluid Lines”, Journal of Basic Engineering, 86(3), 589-598.
[https://doi.org/10.1115/1.3653180]

-
K. Nakano and M. Yoshimoto, 1970, “The Dynamic Characteristics of a Hydraulic Pipe Line with a Viscoelastic Pipe Wall”, Transactions of the Society of Instrument and Control Engineers, 6(3), 201-209.
[https://doi.org/10.9746/sicetr1965.6.201]

-
T. Muto, Y. Kinoshita and R. Yoneda, 1980, “Dynamic Response of Tapered Fluid Lines : 1st Report, Transfer Matrix and Frequency Analysis”, Transactions of the Japan Society of Mechanical Engineers Series B, 46(409), 1705-1712.
[https://doi.org/10.1299/kikaib.46.1705]

- I. Y. Lee, Y. G. Jung and Y. H. Yun, 1995, “Techniques to Reduce Pressure Pulsation in High-Pressure Part and Surge Pressure in Low-Pressure Part of Oil Hydraulic Pipeline System”, Mando Machinery Corporation Central Research Institute.
- I. Y. Lee, Y. G. Jung and K. U. Yang, 1997, “Analysis of Pressure Fluctuations in Oil Hydraulic Pipe Network”, Journal of Ocean Engineering and Technology, 11(4), 152-158.
- I. Y. Lee, S. H. Song, Y. G. Jung and K. U. Yang, 1998, “Development of Analyzing Method for Pressure Fluctuations in Oil Hydraulic Pipe Network including Flexible Hose Element”, Journal of The Korean Society for Power System Engineering, 2(1), 45-51.
- I. Y. Lee, Y. G. Jung and S. J. Lee, 2001, “Attenuation of Pressure Fluctuations in Oil Hydraulic Pipeline with Bellows Type Accumulator”, Journal of The Korean Society for Power System Engineering, 5(4), 31-37.
- Y. W. Mo, Y. T. Yoo, G. D. Na and J. H. Kim, 2004, “A Characteristics of Impedance Propagation by the Unsteady Flow in a Hydraulic Pipeline”, Journal of the Korean Society of Manufacturing Technology Engineers, 13(6), 48-55.
- J. C. Lee and S. H. Oh, 2009, “On the Analytical Model of Automotive Steering Hoses Containing Tuner and Its Practical Application”, Journal of Drive and Control, 6(1), 1-9.
-
D. T. Kim, 2018, “Analysis of Dynamic Characteristics of Hydraulic Transmission Lines with Distributed Parameter Model”, Journal of Drive and Control, 15(4), 67-73.
[https://doi.org/10.7839/ksfc.2018.15.4.067]

-
D. H. Moon and M. S. Choi, 2000, “Vibration Analysis for Frame Structures Using Transfer of Dynamic Stiffness Coefficient”, Journal of Sound and Vibration, 234(5), 725-736.
[https://doi.org/10.1006/jsvi.1999.2970]

-
M. S. Choi and K. U. Yang, 2023, “Static Analysis of Axisymmetric Shells with Various Shapes Using Finite Element-Transfer Stiffness Coefficient Method”, Journal of The Korean Society for Power System Engineering, 27(2), 33-41.
[https://doi.org/10.9726/kspse.2023.27.2.033]

- J. D. King, 2006, “Frequency Response Approximation Methods of the Dissipative Model of Fluid Transmission Lines”, MS thesis, Texas University at Alington, USA.