The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 29, No. 1, pp.30-37

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 28 Feb 2025

Received 30 Aug 2024 Revised 19 Dec 2024 Accepted 19 Dec 2024

DOI: https://doi.org/10.9726/kspse.2025.29.1.030

An Investigation on Optimization of Vertical Hollow Hybrid Fin Heat Sinks with Horizontal Bases in Natural Convection

Wooheon Noh^*

; Kyoung Joon Kim^*^{, †}

*Graduate student, Department of Mechanical Design Engineering, Pukyong National University.
*Professor, Department of Mechanical Design Engineering, Pukyong National University.

Correspondence to: ^†Kyoung Joon Kim : Professor, Department of Mechanical Design Engineering, Pukyong National University. E-mail : kjkim@pknu.ac.kr, Tel : 051-629-6168

Abstract

This study investigates the optimization of vertical hollow hybrid fin heat sinks (HHFHSs) with horizontal bases in natural convection. The HHF is a hollow pin fin integrated with radial plate fins, and the HHFHS consists of the staggered array of HHFs and a horizontal base plate. The Nu correlations for the vertical HHF array were developed using a wide range of thermal data generated by CFD analysis and considering modified Ra, fin efficiency, and geometric parameters of the HHF. The optimization of the HHFHS was established by optimizing both the HHF using the least-material method and the fin spacing using the developed Nu correlations. It has been found that the optimal wall thickness of the HHF is a function of fin volume and structural perimeters. The investigation has proven that the optimal fin spacing of the HHFHS depends on the base length. The investigation has revealed that the thermal performance of the optimized HHFHS is superior to the optimized PFHS at a specific fin mass and a consistent base area.

Keywords:

Hollow Hybrid Fin, Natural Convection, Optimization, Correlation, Heat Sink

1. Introduction

Cost-effectiveness and simplicity enable heat sinks to be an intensively-used thermal management solution in various applications.¹⁾ Drones, LED streetlights, and PV modules are typical thermally-managed electronics by vertical heat sinks with horizontal bases. Both optimum dimensions, allowing the maximum heat dissipation for the least material, and the prediction of thermal performance are crucial for natural convection heat sinks.²⁾

Rigorous investigations have focused on the optimization of the horizontal heat sinks with vertical base plates in natural convection. A single pin fin (PF) was optimized by Sonn et al.³⁾ They employed the least-material optimization method. Rectangular, circular, and triangular horizontal fin arrays were optimized by Bar-Cohen et al.⁴⁾ They utilized the least-material optimization method by considering manufacturability. Thermal behaviors of longitudinal and rectangular fin arrays were also explored under convection conditions.⁵⁾

Our research team explored the performance of the hollow hybrid fin (HHF) and the solid hybrid fin (SHF) heat sinks by comparing with classical PF heat sinks and the comparison was conducted at a fixed volume condition. Our research team developed the method predicting heat transfer around the hollow hybrid fin heat sink (HHFHS).^6,7) As aforementioned, the optimization is a crucial goal for any types of heat sinks including the HHFHS. Hence, in this study, the primary objective is to investigate on the optimization of vertical HHFHSs with horizontal bases in natural convection. It should be noted that this paper is a considerably extended version of a preceding conference presentation.⁸⁾

First, this paper shows the CFD modelling of the HHF and PF arrays under natural convection to generate thermal data. Second, the paper presents the developed Nusselt number correlations of both HHF and PF arrays. Third, the paper shows the development process and the result of least-material optimization for a single HHF. Fourth, the paper presents the optimizing process of the fin spacing of the HHF and PF arrays. Last, the paper shows the thermal performance comparison between the optimized HHFHS and the PFHS.

2. Heat sink structure

This section explains the structure of the HHFHS and the PFHS. The HHFHS consists of a staggered HHF array and a base plate where the HHF has a hollow pin fin integrated with radial plate fins. The PFHS is a staggered pin fin array with a horizontal base plate.

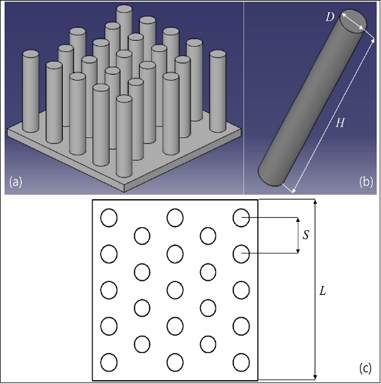
Fig. 1 and Fig. 2 schematically explain the structures of the HHFHS and the PFHS by showing the isometric views of single fins and heat sinks, and the top views of heat sinks. In Figs. 1 and 2, His the fin height, D is the pin fin diameter, D_i is the internal fin diameter, D_o is the external diameter, w_p is the radial plate width, t is the thickness of theradial plate, and S is the fin spacing.

Fig. 1

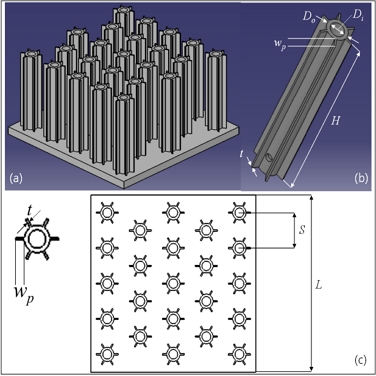
(a) The isometric view of the HHFHS, (b) the isometric view of the HHF, (c) the top view of the HHFHS

Fig. 2

(a) The isometric view of the PFHS, (b) the isometric view of the PF, (c) the top view of the PFHS

The base plate size of the heat sink is 75 × 75 × 5 mm, w_p is 2 mm, and t is 0.5 mm. The number of radial plate fins is 6 for all the configurations. The heat sink material is aluminum 6063.

3. Computational analysis

3.1 Computational fluid dynamics

Computational fluid dynamics (CFD) analysis was conducted utilizing Ansys Fluent to generate a wide range of thermal data of the HHFHS and the PFHS to develop Nusselt number correlations using the data. For a wide range of data, 13 configurations of the HHFHS and 12 configurations of the PFHS were used, and the CFD analysis was conducted at four base temperatures of 50, 70, 90, and 120℃. The configuration variables are summarized in Table 1 where N denotes the number of fins.

Table 1

Summary of HHFHS and PFHS configurations

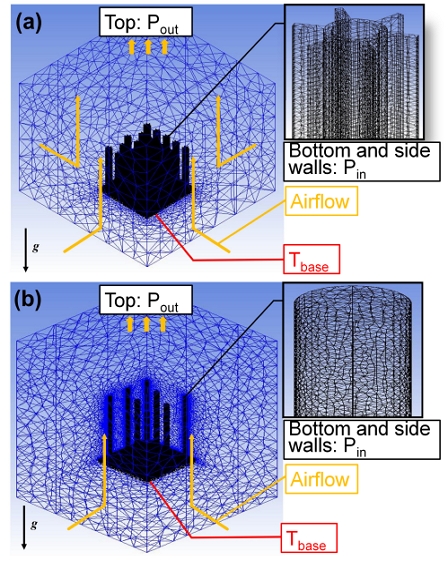
The meshed CFD models and boundary conditions for two types of heat sinks were shown in Fig. 3. For the PFHS, a quarter model was generated to reduce calculation time. About 25 million elements for the HHFHS and 5 million elements for the quarter model of the PFHS were used for mesh generation.

Fig. 3

The CFD model and boundary conditions of (a) the HHFHS and (b) a quarter model of the PFHS

Tetra elements were used, the ambient temperature was selected as 25℃, the ambient pressure was selected as 1 atm, and the solid material was aluminum 6063.

The CFD analysis assumed the steady, incompressible, and laminar flow condition, and negligible thermal radiation. The governing equations for the CFD can be found in references,⁹⁾ and the numerical conditions for the analysis are well shown in the preceding publications.^6,7)

3.2 Nusselt number correlations

The Nusselt number, Nu, and the modified Rayleigh number, Ra' based on the fin spacing, S may describe natural convection around the fin array. They are written as follows

N s = h f i n S k f

(1)

R a ′ s = g γ θ b S 4 Pr L v 2

(2)

Where h_fin is the convection heat transfer coefficient of the fin, k_f is the thermal conductivity of the fluid, g is the gravity, L is the length of the base plate, γ is the volumetric thermal expansion coefficient, θ_b is the temperature difference between the base and the ambient, ν is the kinematic viscosity, and Pr is the Prandtl number. It should be noted again that Ra’_S is the Rayleigh number modified by a base length, L. All the thermal properties are taken at the base temperature.

Nu correlations for the vertical HHF array and the vertical PF array were rigorously developed. For the development, the wide thermal data from CFD analysis for the various configurations, shown in Table 1, with for base temperatures were utilized, and the correlation structure¹⁰⁾ was benchmarked. It should be noted that the correlation of Aihara¹⁰⁾ is for the horizontal PF array.

The developed Nu correlations are shown in Eqn. (3) for the HHF array and Eqn. (4) for the PF array, respectively.

N u H H F a r r a y = 0.000195 D o - D i w p 0.104 D o + D i H 0.075 η R a ′ S 3.29 1 - e - 342 η R a ′ S 1.5 - 291 η R a ′ S - 1.514

(3)

N u P F a r r a y = 1.85 S π D 0.5 0.071 η R a S 0.73 1 - e - 195 η R a S 0.789 + 0.04 η R a S 0.47

(4)

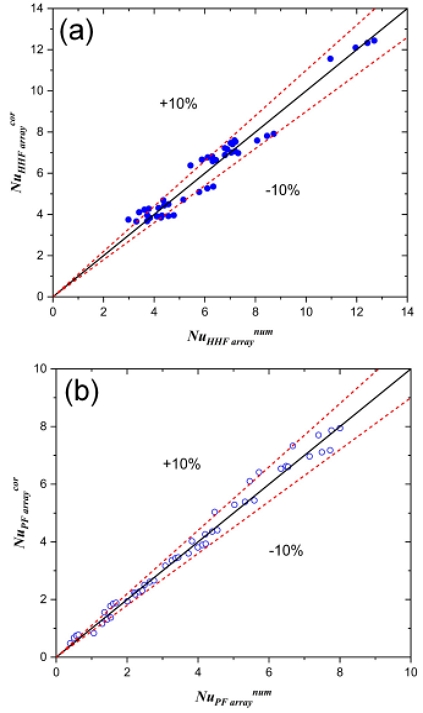
Figs. 4(a) and (b) show the comparison of the Nu numbers obtained by the CFD and the correlation for the HFF and the PF arrays. It is seen that prediction discrepancies of both Nu correlations are within typically 10%. The discrepancy average is seen to be 7.7%. These reasonable discrepancies may validate the Nu correlations.

Fig. 4

Nu determined by the correlation as a function of Nu evaluated by the CFD for (a) the HHF array and (b) the PF array

4. Optimization

The optimization of heat sinks has two steps. Either a HHF or a PF is optimized by the least-material method, and then fin spacing is optimized to dissipate maximum heat rate for the base area.

4.1 Optimum HHF

The optimum pin fin diameter based on the least-material optimization [3] is expressed as

D o p t = 1.366 h f i n V f i n 2 k f i n 15

(5)

The general fin equation for the HHF is expressed as follows.

q f i n = θ b h f i n p k f i n A c tanh ⁡ m H

(6)

Where θ_b is the temperature difference between the fin base and ambient, h_fin is the convection heat transfer coefficient of the fin, p is the perimeter of the fin, k_fin is a fin thermal conductivity, A_c is the cross-sectional area of the fin, and H is the fin height. p and A_c are defined as

p = π D o + D i + 12 w p

(7)

A c = π 4 D o 2 - D i 2 + 6 w p t

(8)

Where w_p and t are the width and thickness of the radially-placed plate pin. In Eqn. (6), m is the eigenvalue of the 1-D fin equation²⁾ and defined as

m = h f i n p k A c

(9)

In this study, the HHF is optimized by determining optimum D_i and D_o. Heat dissipation from radially-placed plate fins are expected to be much smaller than the hollow pin fin. Hence, this investigation did not determine their optimum structures. Substituting Eqn. (9) into (6) and replacing the height as the volume, Eqn. (6) is rewritten as follows. Through this procedure, Eqn. (6) can be expressed as a function of only two variables, D_i and D_o, and it is written in Eqn. (10).

q f i n = θ b h f i n p k f i n A c tanh ⁡ h f i n p k f i n A c 3 V f i n

(10)

By differentiating Eqn. (10) by D_o and D_i and letting two differential equations be zero, following equations are obtained.

∂ q f i n ∂ D o = h f i n p k f i n A c 3 V f i n s e c h 2 h f i n p k f i n A c 3 V f i n - 3 D o 2 + A c P + tanh h f i n p k f i n A c 3 V f i n D o 2 + A c P = 0

(11)

∂ q f i n ∂ D i = h f i n p k f i n A c 3 V f i n s e c h 2 h f i n p k f i n A c 3 V f i n 3 D i 2 + A c P + tanh h f i n p k f i n A c 3 V f i n - D i 2 + A c P = 0

(12)

Substituting β = [(h_finp)/(k_finA_c³)]^0.5V_fin into Eqns. (11) and (12), they are re-expressed as

∂ q f i n ∂ D o = 2 β - 3 D o 2 + A c P + sinh 2 β D o 2 + A c P = 0

(13)

∂ q f i n ∂ D i = 2 β 3 D i 2 + A c P + sinh 2 β - D i 2 + A c P = 0

(14)

Considering Eqns. (13) and (14), a brief relation is obtained as

sinh 2 β = 6 β

(15)

The calculated β, using the trial-error method, is about 1.4192. Using this value, the optimum D_o-D_i is expressed as

D o - D i o p t = 4 π D o + D i h f i n π D o + D i + 12 w p V f i n 2 k f i n β 2 13 - 6 w p t

(16)

It is noteworthy that [(h_fin{π(D_o+D_i)+12w_p} V_fin²)/(k_finβ²)]^1/3 should be greater than 6w_pt because the D_o-D_i is always positive.

4.2 Optimum fin spacing

The total heat dissipation of the heat sink is determined by considering both heat dissipation of the fin array and the heat sink base. It is expressed as

q H S = h f i n A f a η f i n + h b A u b θ b

(17)

Where h_fin and h_fin are the convection heat transfer coefficients of the fin and the heat sink base, A_fa is the surface area of the fin array, A_ub is the net upper surface area of the heat sink base, i.e., the upper surface area of the heat sink base excluding the fin array footprint, η_fin is the fin efficiency, and θ_b is a base excess temperature to the ambient. In Eqn. (17), the fin efficiency, η_fin is defined as

η f i n = tanh ⁡ m H m H

(18)

h_b is determined by considering the correlation for the heat transfer coefficient of an isothermal horizontal plate as follows.

h b = 0.54 k f L R a L 0.25

(19)

The array heat transfer coefficient, h_a, needed for optimization process, is defined as

h a = q H S / A b θ b

(20)

Where A_b is a heat sink base area.

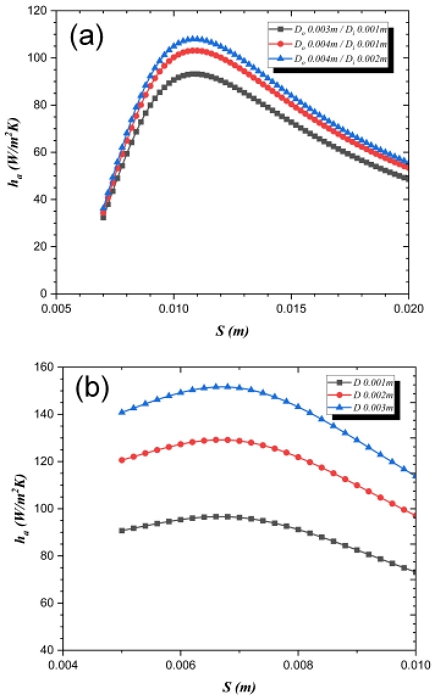
The heat sink base area was selected as 75×75 mm with a consistent base temperature of 70℃ for the optimization condition. The optimum fin spacing was determined by finding the maximum array heat transfer coefficient for various fin spacing values.

Eqns. (1) to (4) and (17) to (20) were utilized to evaluate h_a for S and the results are plotted in Figs. 5(a) and (b). Figs. 5(a) and (b) show a noteworthy finding that for either the HHFHS or the PFHS, the optimum fin spacing value is consistent for each heat sink type despite various configurations.

Fig. 5

The array heat transfer coefficients of (a) the HHFHS and (b) the PFHS as a function of fin spacing

This result suggests that the optimum S is only dependent on the length of the heat sink base. Thus, the optimum S is expressed as follows.

S o p t, P F H S = 2.16 U

(22)

where U is defined as

U = L ν 2 g β η f i n θ b Pr 0.25

(23)

4.3 Thermal performance

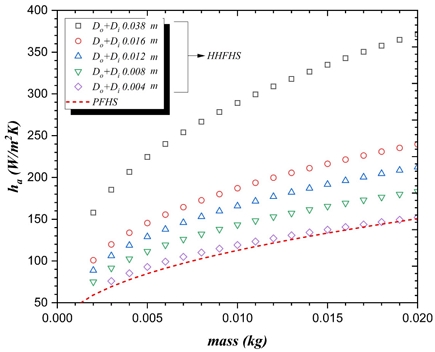
For the optimization, Eqn. (16) and (21) for the HHFHS, and Eqn. (5) and Eqn. (22) for the PFHS were utilized, and 75×75 mm base area and a base temperature of 70℃ were selected for the optimization condition. Fig. 6 shows a representative optimized performance, i.e., array heat transfer coefficient values, for the HHFHS and the PFHS as a function of fin mass. The fin mass ranges from 0.001 kg to 0.02 kg. The result shows that the optimum performance of the HHFHS depends on D_o+D_i. The result also reveals that much less materials could be used to manufacture the HHFHS than the PFHS for a specific thermal performance.

Fig. 6

The array heat transfer coefficients of the optimized HHFHS and PFHS as a function of fin mass

5. Conclusion

This study developed Nu correlations of the vertical HHF array and the PF array under natural convection. Consequently, the study investigated the optimization of the vertical HHFHS and the PFHS associated with the developed Nu correlations. The crucial study results are summarized as follows.

First, Nu correlations for the vertical HHF and PF arrays were rigorously developed by using CFD results. The Nu correlations contain the modified Ra and fin efficiency, and the average prediction discrepancies with CFD results are within 10%. Second, the HHF was optimized analytically by using the least-material method. As a result, the analytical expression of the optimum D_o-D_i for the HHF was obtained. Third, the optimum fin spacing for the HHFHS and the PFHS were determined by finding the maximum array heat transfer coefficient. It is seen that the optimum fin spacing depends on the base length. Last, it has been found that the thermal performance of the optimized HHFHS is superior to the optimized PFHS at a specific fin mass and a consistent base area.

― Nomenclature ―


A :	Area [m²]
A_c :	Cross sectional area [m²]
D :	Diameter [m]
g :	Gravity [m/s²]
H :	Fin height [m]
HS :	Heat sink
h :	Heat transfer coefficient [W/m²K]
k :	Thermal conductivity [W/mK]
L :	Base length [m]
N :	Number of fins
Nu :	Nusselt number
P :	Perimeter [m]
Pr :	Prandtl number
q :	Heat transfer rate [W]
Ra :	Rayleigh number
Ra’s :	Modified Rayleigh number
S :	Fin spacing [m]
t :	hickness of plate fin[m]
U :	Parameter for optimum spacing [m]
V :	Volume [m³]
w_p :	width of plate fin [m]

Greek Symbols


γ :	Volumetric expansion coefficient [1/K]
η :	Efficiency
θ :	Excess temperature to ambient [K]
ν :	Kinematic viscosity [m²/s]
ρ :	Density [kg/m³]

Subscripts


a :	Array
b :	Heat sink base
fa :	Fin array
fin :	Fin
i :	Internal
o :	External
ub :	Upper surface of base

Acknowledgments

This research was supported by a Research Grant of Pukyong National University (2023).

Author contributions

W. Noh; Numerical analysis, Data acquisition, Writing-original draft. K. J. Kim: Conceptualization, Supervision, Writing-review & editing.

References

R. C. Chu, 2005, “The Challenges of Electronic Cooling: Past, Current and Future, Journal of Electronic Packaging”, 126, 491-500. [https://doi.org/10.1115/1.1839594]
A. D. Kraus and A. Bar-Cohen, 1995, Design and Analysis of Heat Sinks, U.S.A: Wiley-Interscience, 239-271.
A. Sonn and A. Bar-Cohen, 1981, “Optimum Cylindrical Pin Fin”, Journal of Heat Transfer, 103, 814-815. [https://doi.org/10.1115/1.3244547]
A. Bar-Cohen, M. Iyengar and S. Benjaafar, 2002, “Design for Manufacturability of Natural Convection Cooled Heat Sinks”, International Journal of Transport Phenomena, 4, 43-57.
A. Bar-Cohen and M. Jelinek, 1985, “Optimum Array of Longitudinal, Rectangular Fins in Convective Heat Transfer”, Heat Transfer Engineering, 6, 68-78. [https://doi.org/10.1080/01457638508939633]
N. S. Effendi, S. S. G. R. Putra and K. J. Kim, 2018, “Prediction Methods for Natural Convection around Hollow Hybrid Fin Heat Sinks”, International Journal of Thermal Sciences, 126, 272-280. [https://doi.org/10.1016/j.ijthermalsci.2018.01.002]
H. H. Yang, W. Noh, S. Jamilah and K. J. Kim, 2023, “An Investigation on Predicting Natural Convection around Hollow Hybrid Fin Arrays”, Journal of Power System Engineering, 27(1), 14-21. [https://doi.org/10.9726/kspse.2023.27.1.014]
W. Noh and K. J. Kim, 2023, “Optimization of Hollow Hybrid Fin Heat Sinks under Natural Convection”, IEEE 29^th Therminic, Sep., 2023, Budapest, Hungary. [https://doi.org/10.1109/THERMINIC60375.2023.10325900]
K. A. Hoffmann and S. T. Chiang, 1998, Computational Fluid Dynamics Volume I, Third ed., Engineering Education System, Wichita, KS.
T. Aihara, S. Maruyama and S. Kobayakawa, 1990, “Free Convective/Radiative Heat Transfer from Pin-Fin Array with a Vertical Base Plate (General Representation of Heat Transfer Performance)”, International Journal of Heat and Mass Transfer, 33, 1223-1232. [https://doi.org/10.1016/0017-9310(90)90253-Q]

Table 1

Summary of HHFHS and PFHS configurations

HHFHS					PFHS
D_o	D_i	H	S	N	D	H	S	N
4	1	20	25	8	1	20	15	23
4	1	20	10	46	1	20	10	46
4	1	75	25	8	3	75	15	23
4	1	75	25	8	3	75	10	46
4	1	200	25	8	3	150	15	23
4	3	20	15	23	3	150	10	46
4	3	75	15	23	10	20	25	8
4	3	200	15	23	10	20	15	23
4	3	200	10	46	10	75	25	8
20	1	20	40	5	10	75	15	23
20	1	75	40	5	20	75	25	8
20	1	200	40	5	20	150	25	8
20	19	75	40	5	-	-	-	-

HHFHS					PFHS
D_o	D_i	H	S	N	D	H	S	N
4	1	20	25	8	1	20	15	23
4	1	20	10	46	1	20	10	46
4	1	75	25	8	3	75	15	23
4	1	75	25	8	3	75	10	46
4	1	200	25	8	3	150	15	23
4	3	20	15	23	3	150	10	46
4	3	75	15	23	10	20	25	8
4	3	200	15	23	10	20	15	23
4	3	200	10	46	10	75	25	8
20	1	20	40	5	10	75	15	23
20	1	75	40	5	20	75	25	8
20	1	200	40	5	20	150	25	8
20	19	75	40	5	-	-	-	-

HHFHS					PFHS
D_o	D_i	H	S	N	D	H	S	N
4	1	20	25	8	1	20	15	23
4	1	20	10	46	1	20	10	46
4	1	75	25	8	3	75	15	23
4	1	75	25	8	3	75	10	46
4	1	200	25	8	3	150	15	23
4	3	20	15	23	3	150	10	46
4	3	75	15	23	10	20	25	8
4	3	200	15	23	10	20	15	23
4	3	200	10	46	10	75	25	8
20	1	20	40	5	10	75	15	23
20	1	75	40	5	20	75	25	8
20	1	200	40	5	20	150	25	8
20	19	75	40	5	-	-	-	-

HHFHS					PFHS
D_o	D_i	H	S	N	D	H	S	N
4	1	20	25	8	1	20	15	23
4	1	20	10	46	1	20	10	46
4	1	75	25	8	3	75	15	23
4	1	75	25	8	3	75	10	46
4	1	200	25	8	3	150	15	23
4	3	20	15	23	3	150	10	46
4	3	75	15	23	10	20	25	8
4	3	200	15	23	10	20	15	23
4	3	200	10	46	10	75	25	8
20	1	20	40	5	10	75	15	23
20	1	75	40	5	20	75	25	8
20	1	200	40	5	20	150	25	8
20	19	75	40	5	-	-	-	-