표면거칠기 예측 성능 향상을 위한 오토인코더 기반 잠재 변수 최적화에 관한 연구

1. 서 론

표면거칠기는 가공품의 표면정도를 나타내는 지표로써 제품의 성능과 품질에 밀접하게 연관되어 있다. 특히 과학 기술이 점진적으로 발전되고 산업계에 적용됨에 따라 초정밀, 초미세 부품 요소들의 수요가 증대되고, 가공품의 표면 개선을 위하여 새로운 표면연마 공정이 개발되고 있다.¹⁾

적용 목적에 따라 요구되는 표면거칠기를 얻기 위하여 일반적으로 실험을 바탕으로 공정 조건을 최적화하고, 수학적 모델을 바탕으로 예측 모델을 정립하는 연구가 진행되었다.^2,3) 그러나 표면연마 공정에서 표면정도 향상에 영향을 주는 공정 변수는 매우 다양하기 때문에 수학적 예측 모델이 표면거칠기와 공정 변수의 상관관계를 명확히 표현하기는 어렵다. 또한 예측 모델의 정확도 향상을 위하여 방대한 양의 실험 데이터가 필요하므로, 실험에 많은 시간이 소요되고 이를 수치적으로 분석하는데 한계가 있다. 이러한 문제점을 극복하고 생산효율을 향상시키기 위하여 최근에는 딥러닝을 바탕으로 표면연마 공정의 비선형적 특성을 분석하고, 이를 바탕으로 예측 모델의 개발에 관한 연구가 활발히 진행되고 있다.^4,5) Soler 등⁶⁾은 적층 제조 공정으로 제작된 Ti-alloy 가공품의 표면 품질 향상을 위하여 심층신경망(Deep neural network, DNN) 활용하여 표면연마 공정에서의 표면거칠기 예측 모델을 개발하였다. 분석 결과, 예측 모델은 약 90%의 정확도를 나타냈으며, 표면거칠기 최적화 조건에서 약 60% 이상 표면정도가 향상됨을 확인할 수 있었다. Guo 등⁷⁾은 음향방출 센서를 통해 실시간으로 공작물의 표면상태를 수집하였다. 수집된 신호를 바탕으로 예측 모델 생성을 위하여 장단기 메모리(Long short-term memory, LSTM) 네트워크를 활용하였다. LSTM에 의한 예측 성능은 99%로 실험 데이터와 유사함을 나타내었다. Ahmad 등⁸⁾은 자기연마 공정에서 DNN 기반 예측 모델을 개발하였고, 공정 최적화를 위하여 유전자 알고리즘을 사용하여 표면거칠기 향상에 영향을 주는 공정 변수의 수준을 결정하였다. Rifai 등⁹⁾은 표면 이미지의 명암을 바탕으로 합성곱 신경망 알고리즘을 활용하여 표면거칠기 예측 모델을 개발하였다. 예측 표면거칠기 값과 실험을 통해 도출된 실제 측정값을 비교한 결과, 10% 이내의 오차를 나타냄으로써 개발된 예측 모델이 적합함을 알 수 있었다.

따라서 본 연구에서는 표면연마 공정과 공정 변수의 상관관계를 분석하고, 정확도 높은 표면거칠기 예측 모델을 제시하기 위하여 비지도 학습인 오토인코더(Autoencoder, AE)와 k-fold 교차 검증을 활용하고자 한다. AE와 k-fold 교차 검증을 통해 주어진 데이터에서 유의미한 특징을 추출한 후, 지도 학습인 DNN의 입력 데이터로 활용하여 회전 전자기 표면연마 공정의 표면거칠기 예측 모델을 제안하고자 한다. 예측 모델의 성능은 AE에서 추출되는 잠재 변수의 개수에 영향을 받으므로 표면거칠기 예측 모델의 최적화를 위하여 잠재 변수의 개수에 따른 예측 모델의 성능을 평가하고자 한다. 또한 AE를 사용하지 않은 DNN 기반 예측 모델과 비교함으로써 제안하는 예측 모델의 신뢰성을 확보하고자 한다.

2. 딥러닝 학습 알고리즘

2.1 오토인코더

오토 인코더(Autoencoder, AE)는 입력 데이터를 압축하여 이들의 특징을 잘 나타낼 수 있는 잠재 변수를 추출하고, 이를 활용하여 출력되는 데이터를 입력 데이터의 형태로 복원시키는 딥러닝의 학습 방법이다. 주어지는 정답 레이블이 없이 학습하기 때문에 비지도 학습으로 분류된다.

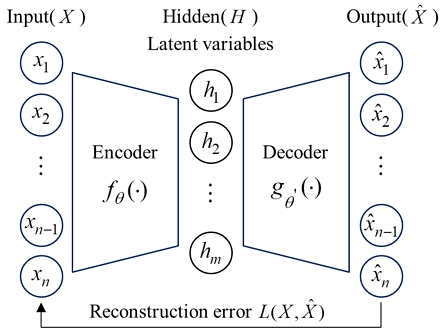
Fig. 1은 기본적인 AE 구조를 도식화한 것으로 입력층, 출력층, 잠재 변수를 포함하는 은닉층으로 구성되어 있다. 입력층의 입력 데이터 $$ \mathit{X}=\left\{x_1,x_2,\cdots ,x_n\right\}$$를 압축하는 과정을 encoder, 복원하여 출력 데이터 $$ \widehat{\mathit{X}}=\left\{{\widehat{x}}_1,{\widehat{x}}_2,\cdots ,{\widehat{x}}_n\right\}$$를 생성하는 과정을 decoder, 압축 과정에서 추출된 입력 데이터의 특징을 나타내는 $$ \mathit{H}=\left\{h_1,h_2,\cdots ,h_n\right\}$$를 잠재 변수라 정의한다. 잠재 변수와 출력 변수는 식 (1)과 식 (2)를 바탕으로 도출된다.

$\[ \mathit{H}=f_{\theta }\left(\mathit{X}\right)=a\left({\mathit{W}}_{\mathit{e}}\mathit{X}+{\mathit{b}}_{\mathit{e}}\right) \]$

(1)

$\[ \widehat{\mathit{X}}=g_{{\theta }^{\prime }}\left(\mathit{H}\right)=a\left({\mathit{W}}_{\mathit{d}}\mathit{H}+{\mathit{b}}_{\mathit{d}}\right) \]$

(2)

Fig. 1

Schematic architectures of autoencoder

여기서, f_θ(.)는 encoder 함수, a(.)는 활성화 함수, g_θ^′(.)는 decoder 함수, $$ \theta =\left\{{\mathit{W}}_{\mathit{e}},{\mathit{b}}_{\mathit{e}}\right\}$$와 $$ {\theta }^{\prime }=\left\{{\mathit{W}}_{\mathit{d}},{\mathit{b}}_{\mathit{d}}\right\}$$는 가중치 W와 편향 b를 포함하는 encoder와 decoder의 매개 변수를 의미한다.

학습 과정에서 입력 데이터와 출력 데이터 간의 차를 손실 함수(L)라 정의하고, 이를 최소화하기 위하여 오차 역전파 알고리즘을 사용하여 식 (3)과 식 (4)와 같이 매개변수인 가중치 W와 편향 b을 조정하여 학습을 진행한다.

$\[ L=\left(\mathit{X},\widehat{\mathit{X}}\right)=\sum _{i=1}^n{‖x_i-{\widehat{x}}_i‖}^2 \]$

(3)

$\[ \theta ,{\theta }^{\prime }=\underset{\theta ,{\theta }^{\prime }}{argmin}L\left(\mathit{X},\widehat{\mathit{X}}\right) \]$

(4)

2.2 k-fold 교차 검증

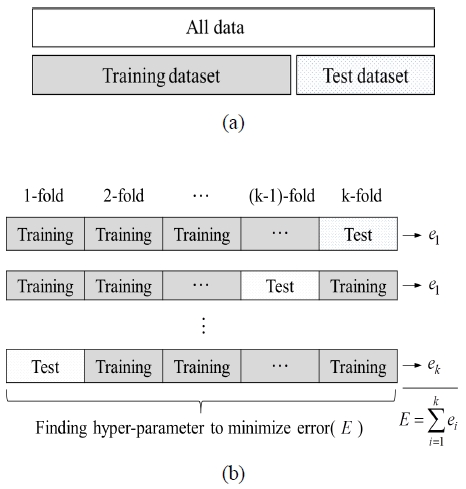
DNN을 바탕으로 예측 모델을 생성하고 정확도를 평가하기 위하여 전체 데이터셋을 일정 비율의 학습 데이터셋과 평가 데이터셋으로 나누는 것은 중요한 단계이다. Fig. 2(a)는 DNN 학습에서 일반적인 데이터셋 분류를 나타낸다. 학습 데이터셋은 예측 모델의 생성에 활용되고, 검증 데이터셋은 생성된 예측 모델의 정확도와 신뢰성을 평가하기 위하여 사용된다. 학습 데이터셋의 비율이 높으면 예측 모델의 정확도는 향상되지만 학습되지 않은 새로운 데이터에 대한 예측의 불확실성이 증가하면서 overfitting 현상이 발생된다. 또한 시간 및 비용 절감을 위하여 모든 경우의 수를 고려한 실험을 수행할 수 없는 경우, 전체 데이터셋은 전체 모집단을 대표할 수 없고, 데이터의 수도 부족하게 된다. 이러한 경우, 편향된 특성을 나타내는 예측 모델이 생성되거나 데이터 부족으로 인한 underfitting 현상이 발생할 수 있다.

Fig. 2

Schematic diagram of (a) typical dividing dataset and (b) k-fold cross validation

위와 같은 문제점을 해결하기 위하여 k-fold 교차 검증을 적용한다. Fig. 2(b)는 k-fold 교차 검증을 간략히 도식화한 것으로, 전체 데이터셋을 k개의 부분집단으로 분류한다. 이 중 k-1개의 부분집단은 학습 데이터셋으로 사용하여 예측 모델을 생성하고, 학습에 참여하지 않은 나머지 하나의 데이터셋은 예측 모델의 신뢰성을 판단하기 위하여 사용된다. 이를 k번 반복하여 수행하고, 도출된 손실 함수의 평균값을 이용하여 예측 모델의 정확도를 평가한다. 일반적인 학습 방법에 비하여 시간이 많이 소요되지만, 적은 데이터 양에 대해 신뢰성이 높은 평가 방법이기 때문에 널리 적용되고 있다.

3. 오토인코더 잠재 변수 최적화

3.1 표면거칠기 데이터 베이스 구축

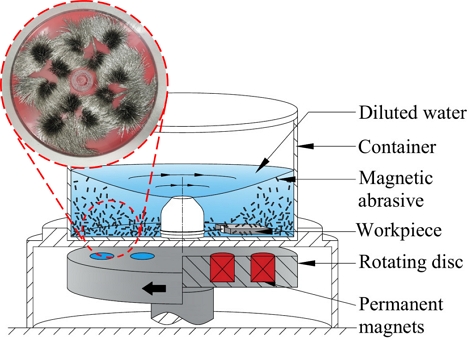
회전 전자기 표면연마 공정은 변화하는 자기장 내에 자화된 연마입자의 운동을 통해 공작물의 표면정도를 향상시키는 비접촉식 표면연마 공정이다. Fig. 3은 회전 전자기 표면연마 장치를 간략하게 나타낸 것으로, 연마공정이 이루어지는 수조 내에는 연마 입자, 공작물, 컴파운드 용액이 있고, 자기에너지를 발생시키는 자기 디스크, 이를 회전시켜 자기력의 변화를 일으키는 구동부로 구성되어 있다.

Fig. 3

Apparatus of rotating electro-magnetic abrasive finishing

본 연구에서는 Al6061의 표면정도 향상을 위하여 표면거칠기 향상에 직접적으로 영향을 미치는 연마 입자의 운동에너지와 자기에너지를 증대시키는 인자를 공정 변수로 선정하였다. 선정된 공정 변수는 회전 디스크의 회전 속도, 연마 입자의 무게, 연마 입자의 직경, 공정 시간이다. 회전 속도(A)는 기계 장치의 운전사양을 고려하여 1,200, 1,500, 1,800 rpm으로 선정하였다. 연마 입자의 무게(B)와 직경(C)는 각각 1.0, 1.5, 2.0 kg과 0.3, 0.5, 0.7 mm로 정하였고, 공정 시간(D)은 5, 10, 15 min으로 설정하였다. 연마 입자는 길이가 3 mm인 원통형 형상이고 재질은 STS304이다.

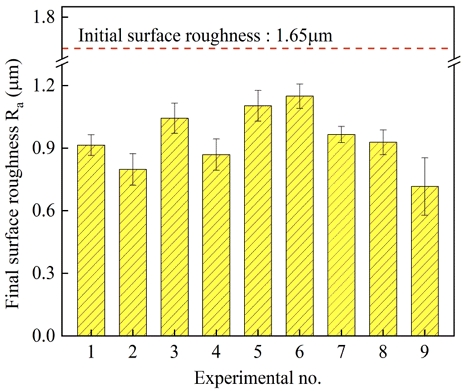
선정된 공정 조건을 바탕으로 Table 1과 같이 다구찌 직교배열법 L₉(3⁴)에 따라 4회 반복하여 총 36회의 실험을 수행하였다. Fig. 4는 각 공정 조건에 따른 실험 후 Al6061의 표면거칠기 값을 나타낸 것이다. 실험 결과, 회전 속도가 1,800 rpm, 연마 입자의 무게와 직경이 각각 2.0 kg과 0.5 mm, 공정 시간이 5 min일 때 평균 표면거칠기를 대표하는 R_a값이 1.65 μm에서 0.72 μm로 감소하여 가장 우수한 표면을 얻을 수 있었다. 본 실험 결과를 바탕으로 4개의 공정 변수와 초기 표면거칠기는 DNN 예측모델의 생성을 위하여 입력 변수로 활용되고, 표면거칠기 값은 예측모델의 정확도 분석을 위하여 출력값의 비교 변수로 활용된다.

Table 1

Experimental factors and levels

Fig. 4

Experimental results of surface roughness

3.2 예측 모델 최적화를 위한 알고리즘

본 연구에서는 AE 학습을 바탕으로 잠재 변수의 개수가 표면거칠기 예측 모델에 미치는 영향을 분석하고 그에 따른 성능을 평가하였다. Table 2는 AE를 통해 추출된 잠재 변수의 개수와 이를 활용한 DNN의 구조를 나타낸 것이다.

Table 2

Detailed structures of deep learning

AE는 대표적인 비지도 학습모델로, 입력층과 출력층의 유사성 분석을 통해 입력층의 특징을 표현하는 잠재 변수를 추출한다. 따라서 AE의 구조는 입력층, 잠재 변수를 포함하는 은닉층, 출력층으로 구성되어 있다. 입력층은 3.1절에 기술한 바와 같이 실험에서 선정된 4개의 공정 변수와 공작물의 초기 표면거칠기를 바탕으로 5개의 노드로 구성하였고, 입력층과 유사성을 분석하기 위하여 알고리즘을 통해 추출되는 출력층의 수는 입력층과 동일한 수로 구성된다. 입력 데이터는 각기 다른 정보와 범위를 가지기 때문에 별도의 전처리 과정 없이 학습에 사용하면 예측 모델의 편향이 발생된다. 따라서 이러한 문제점을 해결하기 위하여 모든 입력 데이터는 정규화 과정을 통해 0과 1 사이의 값으로 변환하여 사용하였다. AE의 성능, 즉 입력층과 출력층의 유사성은 잠재 변수의 정보에 따라 달라지므로, 표면거칠기 예측모델의 최적화를 위하여 잠재 변수의 개수를 2~5개로 변화시켜 학습을 진행하였다. Encoder와 은닉층의 활성화 함수는 sigmoid 함수를 decoder는 ReLU 함수를 적용하였다. 또한 손실 함수인 평균 제곱 오차(Mean squared error, MSE)를 최소화하기 위하여 Adam optimizer를 활용하여 학습을 진행하였다. 회전 전자기 표면연마 공정에 적합한 표면거칠기 예측 모델을 생성하기 위하여 AE 학습을 통해 입력변수의 특징을 대표하는 잠재 변수를 DNN 구조의 입력층으로 활용하였다. DNN의 구조는 입력층, 2개의 은닉층, 출력층으로 구성된다. 잠재 변수의 수에 따른 예측 모델의 정확도를 분석하기 위하여 은닉층의 수는 모든 모델에서 동일하게 5개로 선정하였다. 또한 출력층은 표면거칠기 예측값을 나타내므로 1개로 구성된다. Model 1은 AE를 활용하지 않고 DNN에만 의존하는 예측 모델로 다른 AE-DNN 기반 구조들과의 예측 성능 비교를 위하여 적용되었다.

예측 모델의 생성 및 평가에 사용되는 전체 데이터셋은 실험 데이터를 바탕으로 한다. 딥러닝 학습은 데이터를 바탕으로 수행되기 때문에 예측 모델의 정확도 향상을 위하여 많은 양의 데이터 확보가 필수적이다. 그러나 비용과 시간적 제약으로 인해 모든 경우의 수를 고려한 실험을 진행할 수 없으므로, 적은 데이터로도 효과적으로 학습할 수 있는 6-fold 교차 검증을 적용하였다.

4. 표면거칠기 예측 모델 성능 평가

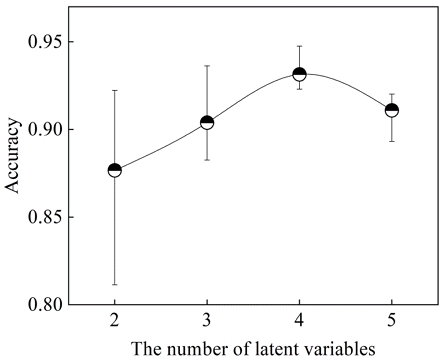
Fig. 5는 AE 학습을 통해 입력 데이터에서 추출된 잠재 변수의 개수에 따른 예측 모델의 정확도를 도시화한 것이다. 학습 결과, 잠재 변수의 개수가 2개일 때 입력 데이터값과 출력 데이터값의 일치도가 87.7%로 가장 낮음을 확인할 수 있었다.

Fig. 5

Accuracy between input and output variables of Autoencoder

이는 5개의 입력 데이터를 2개의 특징으로 나타내는 것이 적절하지 않은 것으로 판단할 수 있다. 반면 잠재 변수의 개수가 4개일 때 가장 높은 정확도인 93.1%를 도출하였다. 이는 잠재 변수의 개수가 증가할수록 손실 함수가 감소하는 경향을 나타낸다. 그러나 입력 데이터의 수와 동일한 잠재 변수의 개수를 가질 경우, 손실 함수가 증가함으로써 정확도가 감소하는 경향을 보였다. 따라서 AE의 학습 결과를 바탕으로 예측 모델의 정확도 향상과 효율적인 학습을 위하여 입력 데이터의 특징을 잘 표현할 수 있는 적절한 잠재 변수 개수의 선정이 중요함을 알 수 있었다.

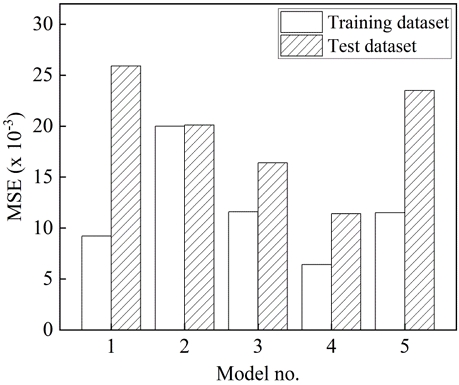
본 연구에서 제안하는 회전 전자기 표면연마 공정에 적합한 표면거칠기 예측 모델을 제시하기 위하여, AE에서 추출된 잠재 변수를 활용하여 DNN을 기반으로 학습을 수행하였다. 표면거칠기 예측 모델의 정확도는 학습모델을 통해 계산된 값과 실제 실험값과의 오차를 나타내는 MSE로 평가하였고, MSE 값이 작을수록 표면거칠기 예측 모델의 정확도가 증대되는 것으로 판단할 수 있다. 학습된 모델의 MSE 결과값은 Fig. 6과 같이 나타낼 수 있다. Fig. 5에 도시된 결과를 바탕으로 AE 기반 학습모델에서 추출된 잠재 변수의 개수가 4개일 때 입력 데이터의 특징을 잘 표현했기 때문에 이를 DNN의 입력 데이터로 활용한 model 4의 표면거칠기 예측 모델이 가장 높은 정확도를 나타내었다. model 4의 경우, 학습 알고리즘을 통해 도출된 학습 데이터셋의 MSE는 6.4×10^-3, 예측 모델의 정확도와 신뢰성 검증을 위해 사용된 검증 데이터셋의 MSE는 11.4×10^-3으로, 다른 예측 모델 대비 가장 낮게 나타남으로써 수행한 실험값에 가장 유사한 결과를 나타내었다. 이는 생성된 예측 모델이 회전 전자기 표면연마 공정에 적합한 것으로 판단할 수 있다. 적합한 표면 비지도 학습인 AE를 활용하지 않은 model 1의 경우, model 2, 3, 5보다 학습 데이터셋의 MSE는 낮게 도출되었지만 검증 데이터셋의 MSE는 25.9×10^-3 로 다른 모델 대비 높게 나타남을 알 수 있었다. 이는 지도 학습만을 이용하여 예측 모델을 생성할 경우, 학습 데이터셋에 대한 표면거칠기의 예측 성능은 우수하지만 학습되지 않은 새로운 데이터에 대해서는 overfitting이 발생하여 표면거칠기와 공정 변수와의 상관관계를 제대로 표현하는데 한계가 있음을 의미한다.

Fig. 6

Prediction performance of surface roughness

5. 결 론

본 연구는 회전 전자기 표면연마 공정에 적합한 표면거칠기 예측 모델을 도출하기 위하여 딥러닝 학습 방법을 활용하였다. 비지도 학습인 AE와 k-fold 교차 검증을 통해 공정 변수의 특징을 잘 표현할 수 있는 잠재 변수의 개수를 분석하고 이를 DNN 학습에 활용하여 표면거칠기 예측 모델을 도출하였다. 본 연구를 통해 얻어진 결론은 다음과 같다.

1) AE 은닉층의 잠재 변수 개수가 증가할수록 입력 데이터와 출력 데이터 간의 손실 함수가 감소함을 확인하였다. 그러나 잠재 변수의 개수가 입력 데이터와 동일하면 추출된 특징이 입력 데이터를 정확히 표현하는데 한계가 있음을 알 수 있었다.

2) DNN 기반 표면거칠기 예측 모델의 성능 비교 결과, AE 학습에서 손실 오차가 가장 작은 잠재 변수의 개수가 4개인 model 4가 예측 정확도가 가장 높았다. 반면 손실 오차가 가장 크게 도출된 잠재 변수의 개수가 2개인 model 2의 예측 정확도가 가장 낮음을 확인할 수 있었다.

3) DNN 학습만을 고려한 예측 모델의 학습 데이터셋의 MSE는 9.2×10^-3, 검증 데이터셋의 MSE는 25.9×10^-3으로 도출되었다. AE-DNN 기반 model 4의 MSE와 비교 결과, 각각 1.5배와 2배 이상 손실 함수 값이 크게 나타남을 확인할 수 있었다.

Author contributions

J. H. Lee; Conceptualization, investigation, writing- original draft. J. S. Kwak; Writing-review & editing.

References

• A. W. Hashmi, H. S. Mali, A. Meena, K. K. Saxena, S. Ahmad, M. K. Agrawal, B. Sagbas, A. P. V. Puerta and M. I. Khan, 2023, “A Comprehensive Review on Surface Post-treatments for Freeform Surfaces of Bio-implants”, Journal of Materials Research and Technology, 23, 4866-4908. [https://doi.org/10.1016/j.jmrt.2023.02.007]
• T. Misaka, J. Herwan, O. Ryabov, S. Kano, H. Sawada, N. Kasashima and Y. Furukawa, 2020, “Prediction of Surface Roughness in CNC Turning by Model-assisted Response Surface Method”, Precision Engineering, 62, 196-203. [https://doi.org/10.1016/j.precisioneng.2019.12.004]
• A. Misra, P. M. Pandey, U. S. Dixit, A. Roy and V. V. Silberschmidt, 2019, “Multi-objective Optimization of Ultrasonic-assisted Magnetic Abrasive Finishing Process”, International Journal of Advanced Manufacturing Technology, 101, 1661-1670. [https://doi.org/10.1007/s00170-018-3060-0]
• V. Pandiyan, S. Shevchik, K. Wasmer, S. Castagne and T. Tjahjowidodo, 2020, “Modelling and Monitoring of Abrasive Finishing Processes Using Artificial Intelligence Techniques: A Review”, Journal of Manufacturing Processes, 57, 114-135. [https://doi.org/10.1016/j.jmapro.2020.06.013]
• H. Yang, H. Zheng and T. Zhang, 2024, “A Review of Artificial Intelligent Methods for Machined Surface Roughness Prediction”, Tribology International, 109935. [https://doi.org/10.1016/j.triboint.2024.109935]
• D. Soler, M. Telleria, M. B. García-Blanco, E. Espinosa, M. Cuesta and P. J. Arrazola, 2022, “Prediction of Surface Roughness of SLM Built Parts After Finishing Processes Using an Artificial Neural Network”, Journal of Manufacturing and Materials Processing, 6(4), 82. [https://doi.org/10.3390/jmmp6040082]
• W. Guo, C. Wu, Z. Ding and Q. Zhou, 2021, “Prediction of Surface Roughness Based on a Hybrid Feature Selection Method and Long Short-term Memory Network in Grinding”, International Journal of Advanced Manufacturing Technology, 112, 2853-2871. [https://doi.org/10.1007/s00170-020-06523-z]
• S. Ahmad, R. M. Singari and R. S. Mishra, 2021, “Tri-objective Constrained Optimization of Pulsating DC Sourced Magnetic Abrasive Finishing Process Parameters Using Artificial Neural Network and Genetic Algorithm”, Materials and Manufacturing Processes, 36(7), 843-857. [https://doi.org/10.1080/10426914.2020.1866196]
• A. P. Rifai, H. Aoyama, N. H. Tho, S. Z. M. Dawal and N. A. Masruroh, 2020, “Evaluation of Turned and Milled Surfaces Roughness Using Convolutional Neural Network”, Measurement, 161, 107860. [https://doi.org/10.1016/j.measurement.2020.107860]