무인기 이착륙 충격 감소를 위한 비주얼 서보잉기반 모션플랫폼 임피던스 제어

1. 서 론

무인항공기(Unmanned Aerial Vehicle, UAV)는 높은 범용성과 활용도를 인정받아 인간이 수행하기 어려운 험지 탐사, 해양조사 등 그 활용범위가 꾸준히 넓어지고 있다. 이와 관련하여 최근 자율주행 기술이 발전하며 적용 대상으로 UAV를 활용하는 연구가 증가하고 있다.¹⁾

그러나 UAV의 사업 규모가 증가함에 따라서 관련 사고가 증가하고 있으며, 전체 UAV 사고의 원인으로 32%가 기체 결함이고, 약 78%가 이/착륙 시 발생한다.²⁾ 이는 UAV의 내구성과 이/착륙이 기체의 안전에 중요함을 나타내고 있다. 이를 해결하기 위해 Hogan^3,4)은 측정된 엔드 이펙터(end-effector)의 위치, 속도 및 힘을 기반으로 제어기의 엔드 이펙터 임피던스를 제어하는 방법을 제안했다. S. Tachi⁵⁾는 힘 센서 없이 직접 구동방식의 매니퓰레이터에 대한 임피던스 제어 방식을 제안하여 관성, 감쇠, 강성 요소를 기반으로 한 임피던스 제어를 통해 외부 접촉에 유연하게 대응하는 제어구조를 소개했다. Z. W. Luo⁶⁾는 동적 환경에서 매니퓰레이터의 감쇠, 강성이 변화하는 임피던스 제어를 통하여 외란과 불안정성을 줄일 수 있도록 개선하였다. Toshio Tsuji⁷⁾는 시각적 피드백을 통해 환경의 특성에 맞추어 동작할 수 있는 비접촉 임피던스 제어 방식을 다루었다.

따라서 본 논문에서는 모션 플랫폼에서 UAV 착륙 시 발생하는 충격을 최소화하는 비전 기반 임피던스 제어(Vision Based Impedance Control, VBIC)와 이미지 기반 비주얼 서보잉(Image Based Visual Servoing, IBVS)을 통해 안전한 착륙공간을 제공하는 제어기법에 대해 제안한다. 비전 기반 임피던스 제어를 모션플랫폼에 적용하고, 기구학적 중복성을 활용할 수 있는 비접촉 임피던스 제어를 활용하여 이/착륙 충격을 최소화한다.

2. 모델링

2.1 역기구학 모델링

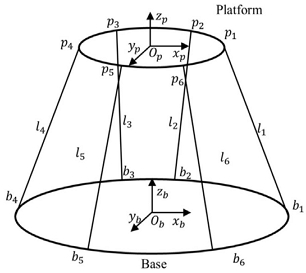
시스템은 무인기의 동특성을 고려하여 Stewart platform 또는 Hexapod라고 불리는 6축 모션플랫폼으로 선정하였다.⁸⁾ 모션플랫폼은 고정된 하판 베이스(Base)와 움직이는 상판 플랫폼(Platform)인 6개의 다리로 Fig. 1과 같이 구성된다.

Fig. 1

The schematic diagram of the Stewart platform system

하판인 베이스와 상판인 플랫폼의 좌표계를 해석하기 위해, 플랫폼 좌표계는 원점 O_p을 기준으로 좌표계 (x_p,y_p,z_p)로 정의했으며, 베이스 좌표계는 원점 O_b를 기준으로 좌표계(x_b,y_b,z_b)로 정의된다. 두 좌표계의 원점은 Fig. 1과 같이 각각 베이스와 플랫폼의 중심에 있으며, p_i와 b_i (i = 1,2,...,6)은 조인트 위치이다. l_i는 전체 다리의 길이를 나타낸다. 플랫폼의 위치와 자세는 $$ \mathit{q}={\left(x,y,z,\varphi ,\theta ,\psi \right)}^T$$로 정의되며 여기서 x,y,z는 3차원 위치를 나타내고, ϕ,θ,ψ는 x,y,z좌표계에서 플랫폼의 유클리드 각도를 나타낸다.

일반적인 모션플랫폼의 역기구학은 주어진 위치 및 자세 q에 대해 각 다리의 길이를 계산하는 과정을 나타낸다. 각 다리의 길이는 다음과 같이 계산할 수 있다.

$\[ l_i=‖\left(R{p}_i+T\right)-b_i‖ \]$

(1)

여기서, R은 회전행렬, T는 변환행렬이다.

3. 제어기 설계

3.1 PID 제어기 설계

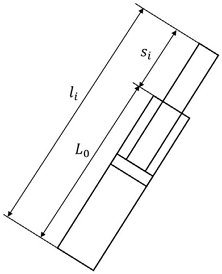
Fig. 2는 다리의 모습을 나타낸다. 여기서 L₀는 하우징의 길이, s_i는 스트로크의 길이다. 스트로크의 길이는 다음과 같이 나타낼 수 있다.

$\[ s_i\left(t\right)=l_i\left(t\right)-L_0 \]$

(6)

Fig. 2

Diagram of one of the six legs

식 (6)에서 설계된 값과 실제 값의 오차를 다음과 같이 나타낼 수 있다.

$\[ s_{ei}\left(t\right)=s_{di}\left(t\right)-s_i\left(t\right) \]$

(7)

$\[ {\dot{s}}_{ei}\left(t\right)={\dot{s}}_{di}\left(t\right)-{\dot{s}}_i\left(t\right) \]$

(8)

식 (7)과 식 (8)을 이용하여, 다리의 힘 F_l는 PID 제어에 의해 다음과 같이 나타낼 수 있다.¹⁰⁾

$\[ F_l=K_P{s}_{ei}\left(t\right)+K_I\int s_{ei}\left(\tau \right)d\tau +K_D{\dot{s}}_{ei}\left(t\right) \]$

(9)

여기서, K_P,J_I와K_D는 각각 비례 이득, 적분 이득과 미분 이득이다.

3.3 임피던스 제어

앞서 계산된 식 (11)과 식 (12)을 이용하여 다음과 같은 수식을 얻을 수 있다.

$\[ a={\ddot{\mathit{q}}}_d+M_m^1\left[D_m\left({\dot{\mathit{q}}}_d-\dot{\mathit{q}}\right)+K_m\left({\mathit{q}}_d-\mathit{q}\right)-F_r\right] \]$

(13)

여기서, q_d는 설계된 동작이고, M_m과 D_m, K_m은 각각 플래폼이 갖는 질량, 스프링계수, 댐핑계수이다. 식(13)을 정리하면 다음과 같다.

$\[ F_r=M_m\left({\ddot{\mathit{q}}}_e\right)+D_m\left({\dot{\mathit{q}}}_e\right)+K_m\left({\mathit{q}}_e\right) \]$

(14)

여기서, q_d - q = q_e이다.

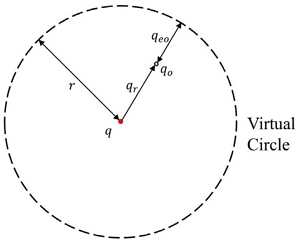
Fig. 3에서 q_o는 객체의 위치, r은 가상 원의 반지름, q_r은 객체와 플랫폼 중심점의 거리, q_eo는

Fig. 3

Virtual circle of vision-based impedance control system

q_o와 가상원의 거리이다. q_eo의 조건은 식 (15)와 같다.

$\[ {\mathit{q}}_{eo}=r\mu -{\mathit{q}}_r \]$

(15)

여기서, μ는 |q_r| ≠ 0일 땐, $$ \frac{q_r}{\left|q_r\right|}$$이고, |q_r| = 0일 땐 0이다.

가상의 비전 센서에 의해 계산된 힘 F_v는 다음과 같이 정의할 수 있다.

(16)

정리하면, 모션플랫폼과 객체에 대한 임피던스 제어기는 다음과 같이 주어진다.

$\[ a={\ddot{\mathit{q}}}_d+M_m^1\left[D_m\left({\dot{\mathit{q}}}_d-\dot{\mathit{q}}\right)+K_m\left({\mathit{q}}_d-\mathit{q}\right)-F_r-F_v\right] \]$

(17)

식 (17)을 정리하면 다음과 같은 수식으로 나타낼 수 있다.

$\[ F_r+F_v=M_m\left({\ddot{\mathit{q}}}_e\right)+D_m\left({\dot{\mathit{q}}}_e\right)+K_m\left({\mathit{q}}_e\right) \]$

(18)

동작경로를 도출하기 위해서, μ와 q_d가 상수라고 가정하고, 식 (18)에 식 (16)를 대입하면,

$\[ \begin{array}{c}\left(M_m+M_o\right)\ddot{\mathit{q}}+\left(D_m+D_o\right)\dot{\mathit{q}}+\left(K_m+K_o\right)\mathit{q}\hfill \\ =-\left[M_o{\ddot{\mathit{q}}}_o+D_o{\dot{\mathit{q}}}_o+K_o{\mathit{q}}_o\right]\hfill \end{array} \]$

(19)

여기서, M_m + M_oM^', D_m + D_o = D^' 그리고 K_m + K_o = K^'로 두고, 식 (19)를 라플라스 변환하면 시스템의 전달함수는 다음과 같다.

$\[ \frac{\mathit{q}\left(s\right)}{{\mathit{q}}_{\mathit{o}}\left(s\right)}=-\frac{M_o{s}^2+D_{o}s+K_o}{M^{\prime }{s}^2+D^{\prime }s+K^{\prime }} \]$

(20)

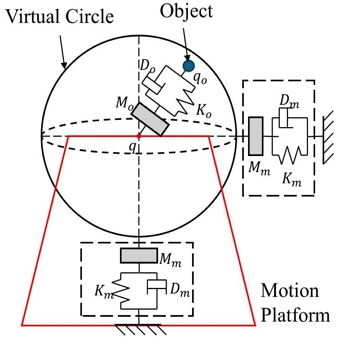
계산된 전달함수는 Fig. 4와 같이 비전기반 임피던스 제어를 적용한 모션플랫폼에서 사용된다.

Fig. 4

Schematic representation of a vision-based impedance control

4. 시뮬레이션

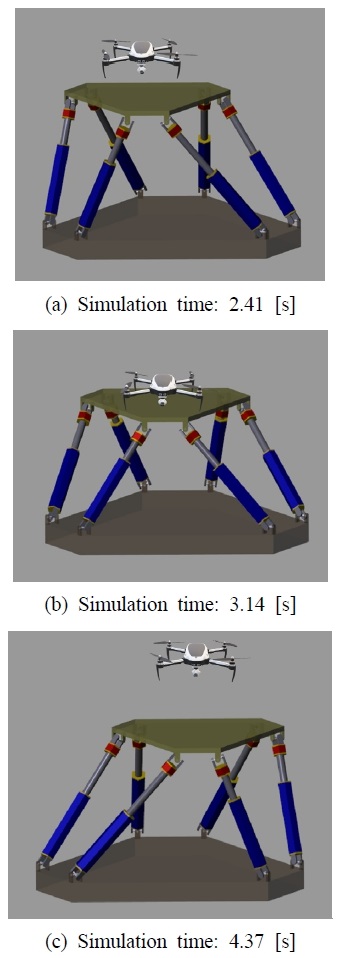
시뮬레이션에서는 본 논문에서 제안하는 세가지 제어기를 적용하여 모션플랫폼의 동작을 평가한다. 시뮬레이션을 위한 MATLAB/Simulink에서 사용된 파라미터는 Table 1에 정의되었으며, Fig. 5는 지름 30 cm의 원을 그리며 낙하하는 오브젝트와 동작을 수행하는 모션플랫폼을 나타내었다.

Table 1

Simulation parameters

Fig. 5

Motion platform simulation

Fig. 6을 통해 시뮬레이션에서 모션플랫폼이 동작하는 것을 확인할 수 있다.

Fig. 6

Platform trajectories variation for the object

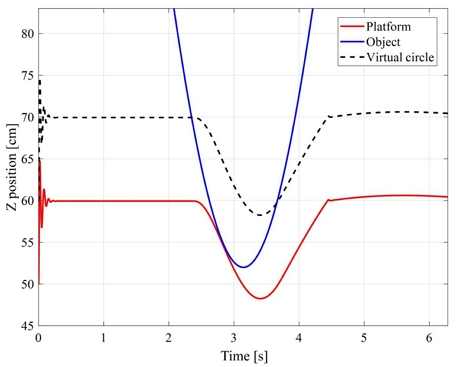
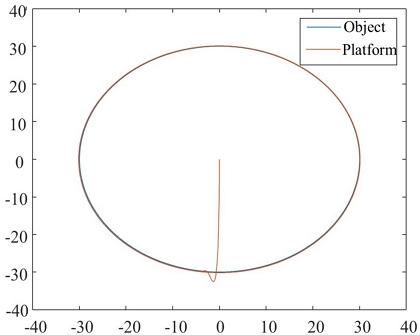
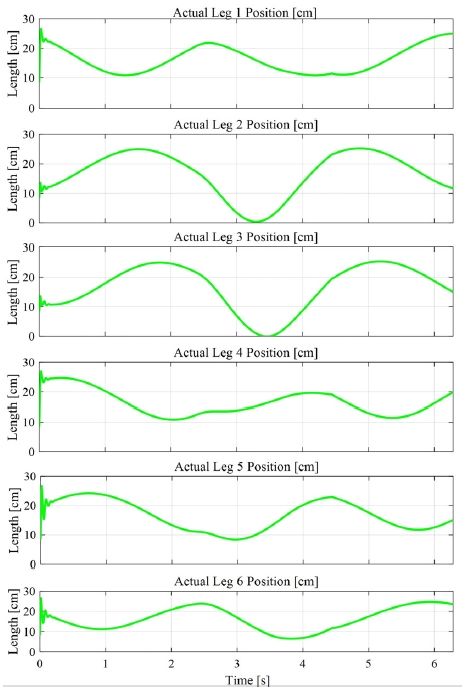
Figs. 6~8에서 시뮬레이션의 결과를 보여 주고 있다. Fig. 6은 Object가 Offset. 즉, Vitual Circle의 범위 안에 진입하면 가상 임피던스에 의해 비전기반 임피던스 제어를 수행하는 것을 나타낸다. Fig. 6에 나타난 것과 같이 객체가 접근하자 플랫폼이 11.5 cm 하강하여 착륙 충격을 완화하는 모습을 볼 수 있다. Fig. 7은 IBVS를 수행하는 모션플랫폼의 궤적과 Object의 궤적을 X-Y그래프에 나타낸다. Fig. 7에 나타난 것과 같이 비주얼 서보잉은 RMS 97%의 추종 정확도가 나타났다. Fig. 8은 각 다리의 길이에 대한 변화를 나타낸다. Fig. 8을 통해 각 다리의 동작 성능을 확인할 수 있다.

Fig. 7

IBVS X-Y Graph (Top view)

Fig. 8

Variation of the leg lengths

5. 결 론

본 논문은 무인기 이착륙 시 발생하는 충격을 감소시키기 위해 모션플랫폼이 비전기반 임피던스 제어, 비주얼 서보잉 제어와 역기구학 기반 PID제어기를 통해 동작하는 시스템을 제안하였다. MATLAB을 통해 시뮬레이션을 구축하였고, 시뮬레이션 결과 무인기의 위치를 추정하여 안정적으로 추종 정확도 RMS 97%의 비주얼 서보잉을 수행하였으며, 무인기의 착륙 충격을 감소시키기 위해 플랫폼이 11.5 cm 하강하여 안전한 착륙공간을 제공하는 것으로 나타난다. 향후 연구에서는 시뮬레이션을 바탕으로 실제 모션플랫폼을 제작하고 실험을 수행하여, 제안하는 시스템에 대한 실효성을 검증할 예정이다.

Acknowledgments

이 논문은 2023년도 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임. (RS-2023-00257498, 모션플랫폼이 적용된 선박용 비접촉식 지능형 무인기 점검 플랫폼)

This research was supported by Korea Institute of Marine Science & Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries, Korea (RS-2023-00257498).

References

• Q. Hailong et al., 2019, “Autonomous Exploration and Mapping System Using Heterogeneous UAVs and UGVs in GPS-Denied Environments”, IEEE Transactions on Vehicular Technology, 68, 1339-1350. [https://doi.org/10.1109/TVT.2018.2890416]
• A. Muhammad et al., 2010, “Probable Casual Factors in UAV Accidents Based on Human Factor Analysis and Classification System”, International Congress of the Aeronautical Sciences.
• N. Hogan et al., 1985, “Impedance Control: An Approach to Manipulation, Parts I, 11, 111”, ASME Journal of Dynamic Systems, Measurement, and Control, 107(1), 1-24. [https://doi.org/10.1115/1.3140702]
• N. Hogan et al., 1987, “Stable Execution of Contact Tasks Using Impedance Control”, Proc. of IEEE International Conference on Robotics and Automation, 1047-1054. [https://doi.org/10.1109/ROBOT.1987.1087854]
• S. Tachi et al., 1991, “Impedance Control of a Direct-Drive Manipulator without Using Force Sensors”, Advanced Robotics, 5(2), 183-205. [https://doi.org/10.1163/156855391X00151]
• Z. W. Luo et al., 1993, “Control Design of Robot for Compliant Manipulation on Dynamic Environments”, IEEE Trans. on Robotics and Automation, 9(3), 286-296. [https://doi.org/10.1109/ROBOT.1991.131550]
• T. Toshio et al., 1997, “Non-Contact Impedance Control for Redundant Manipulators Using Visual Information”, IEEE, 2571-2576. [https://doi.org/10.1109/ROBOT.1997.619348]
• D. Stewart et al., 1965, “A platform with six degrees of freedom”, Proceedings of the Institution of Mechanical Engineers 180, 371-386. [https://doi.org/10.1243/PIME_PROC_1965_180_029_02]
• H. B. Guo et al., 2006, “Dynamic Analysis and Simulation of a Six D.O.F Stewart Platform Manipulator”, Mechanical Engineering Science, 220(1), 61-72. [https://doi.org/10.1243/095440605X32075]
• W. Y. Choi et al., 2024, “Optimizing Look-Ahead Distance for Vehicle Lateral Control: A Controller-Adaptive Approach”, IEEE Transactions on Intelligent Vehicles, 99, 1-12. [https://doi.org/10.1109/TIV.2024.3488057]
• W. Y. Choi et al., 2021, “On-road Object Collision Point Estimation by Radar Sensor Data Fusion”, IEEE Transactions on Intelligent Transportation Systems, 23(9), 14753-14763. [https://doi.org/10.1109/TITS.2021.3133290]
• F. Chaumetteand et al., 2006, “Visual Servo Control. I. Basic Approaches”, IEEE Robot. Autom. Mag., 13(4), 82-90. [https://doi.org/10.1109/MRA.2006.250573]