충격하중을 받는 링 보강 주름 원통쉘의 동적 응답


초록
충격하중을 받는 링으로 보강되고 주름진 원통쉘의 동적 응답에 대해 이론적 방법을 이용하여 연구하였다. 원통쉘은 쉘의 길이 방향을 따라 일정한 간격으로 링에 의해 보강된다. 또한 균일한 주름의 단면 형상이 쉘의 길이 방향으로 진행되는 길이 방향 주름을 갖는다. 주름 쉘을 해석하기 위해 등가 균질 모델을 이용하였다. 등가 균질 모델은 주름 원통쉘을 직교이방성쉘로 취급한다. 변형 형상 등과 같은 해석 결과에서 보강재의 위치에 따른 영향을 나타내기 위해 각각의 보강재를 개별 객체로 취급하는 이산보강이론을 적용하였다. 제안된 접근방법의 타당성을 검증하기 위해 이론해석을 통해 얻은 처짐에 대한 동적 응답을 ANSYS를 이용한 유한요소해석 결과와 비교하였다.
Abstract
The dynamic response characteristics of ring-stiffened and corrugated cylindrical shells subjected to the impulse load is investigated by the theoretical method. The shells have longitudinal corrugations and are reinforced by ring stiffeners evenly spaced along the shell length. The equivalent homogenization model is used to analyze the mechanical behavior of the corrugated shell. This homogenization model treats a corrugated shell as an orthotropic shell that has different material properties in two perpendicular directions. The discrete stiffening theory is applied, which each stiffener is treated as a discrete element, to predict the local mode to be generated by the presence of stiffeners. To validate the proposed theoretical approach, the dynamic response results from the theoretical method are compared with those from the FEA by ANSYS.
Keywords:
Impulse Load, Corrugated Cylindrical Shell, Equivalent Homogenization Model, Ring Stiffener, Discrete Stiffening Theory키워드:
충격 하중, 주름 원통쉘, 등가 균질 모델, 링 보강재, 이산 보강 이론1. 서 론
두께가 얇은 주름 원통쉘은 높은 에너지 흡수 능력, 높은 압축 강도, 높은 강성 대 무게 비 등 우수한 특성 때문에 항공우주, 조선, 토목, 철도차량, 석유화학 플랜트 및 기타 산업에서 널리 이용되고 있다. 이러한 주름 원통쉘은 외부 폭발, 충돌 등 다양한 형태의 측면 하중을 받을 수 있다. 외부 폭발, 충돌 등은 모두 매우 짧은 시간에 가해지는 충격하중으로 구조물에 작용하게 되면 진동이나 공진을 일으킬 수 있으며, 공진은 피로로 이어져 파괴의 원인이 될 수 있다.1)
주름 원통쉘에 대해 몇몇 연구자들이 연구를 수행하였다. Ross 등은 유한요소법을 이용하여 공기 및 수중에 있는 원주 방향 주름 복합재료 원통쉘에 대해 진동 특성을 분석하였으며, 검증을 위해 일부 시험을 수행하였다.2) Ghazijahani 등은 균일한 외부 압력을 받는 원주 방향 주름 원통쉘에 대해 시험을 통해 좌굴 특성을 연구하였다.3) Kim은 양단이 모두 고정된 길이 방향 주름 원통쉘을 등가 직교이방성쉘로 등가시켜 진동해석을 수행하였다.4) Alkhatib 등은 주름 원추쉘에 대해 실험과 유한요소해석을 통해 충돌 거동에 대한 연구를 하였다.5) Liu 등은 저속 충격하중을 받는 원주방향 주름진 원통쉘에 대해 등가모델을 이용하여 이론적으로 동적 응답에 대해 연구하였다.6)
원통쉘에 주름을 주어 사용할 경우, 주름 방향으로는 매우 유연하기 때문에 구조적으로 취약하게 된다. 따라서 이를 보완하기 위해 주름 횡 방향에 대해 보강재를 이용하여 보강할 필요가 있다. 그러나 보강 주름 원통쉘에 대한 연구는 그다지 많지 않다. Iwicki 등은 쉘의 길이 방향으로 열린 단면 보로 보강된 원통형 사일로에 대해 유한요소법을 이용하여 기하 및 재료 비선형을 고려한 안정성 해석을 수행하였다.7) Maleki 등은 Iwicki 등7)의 모델에 대해 유한요소법을 이용하여 풍하중에 의한 비선형 좌굴에 대해 연구하였다.8) Hajko 등은 열린 단면 보로 보강된 주름 원통 사일로에 대해 국부 및 전역 좌굴 특성을 유한요소법을 이용하여 분석하였다.9) Iwicki 등은 앞서 이들이 다루었던 수직 보로 보강된 주름 원통 사일로7)를 등가모델로 취급하여 좌굴에 대해 유한요소법을 이용한 연구를 수행하였다.10) 보로 보강된 주름 원통쉘에 대한 대부분의 연구는 원주 방향 주름에 대한 것이다. 그러나 고압을 받는 우주 항공용 로켓 구조 등의 다양한 구조 목적에 따라 길이 방향 주름 원통쉘이 이용될 수도 있다.11) 또한 Saturn V 로켓의 표피 일부는 길이 방향 주름 원통쉘로 추가 보강되어 있다. 이처럼 길이 방향 주름 원통쉘은 축 방향 압축 및 굽힘강성이 매우 우수한 구조 요소로써 외부 충격하중에 대한 동적 거동을 이해할 필요가 있다. 그러나 주름 구조의 기하학적인 형상 때문에 이론적으로 해석하는 것은 매우 어렵다. 유한요소법을 이용하면 복잡한 구조물 해석에 적용할 수 있다는 장점은 있으나 3차원으로 모델링을 할 때 많은 시간이 요구되며, 구조가 변경될 때마다 모델링을 수정하여야 하는 등 많은 번거로움이 있다. 이와 같은 이유로 주름 구조물의 전체적인 응답을 보다 쉽게 분석하기 위한 이론해석에서는 주름진 구조물 2차원 직교 이방성 재료로 등가시켜 거동을 분석하고 있다.
이상에서처럼 주름 원통쉘에 대한 연구는 대부분 유한요소법을 이용하고 있으며, 이론적 방법에 관한 연구는 매우 찾아보기 힘들다. 특히 링 보강 주름 원통쉘에 대한 연구는 전혀 없는 상태이다. 따라서 본 연구에서는 링으로 보강된 길이 방향 주름 원통쉘에 대해 외부 충격하중에 의한 동적 응답 특성을 이론적으로 얻고자 한다. 이론해석에서는 주름 원통쉘을 균질 모델인 직교 이방성 원통쉘로 등가시켜 해석을 수행하였다. 보강재의 위치에 따른 영향을 나타내기 위해 보를 개별 요소로 취급하는 이산 보강 이론을 적용하였다. Rayleigh- Ritz 법과 변분 원리를 적용하여 운동방정식을 유도하였으며, 동적 특성을 구하기 위해 Mathematica를 이용하여 프로그램을 작성하였다. 한편 이론 해의 타당성을 검증하기 위해 상용 유한요소 프로그램인 ANSYS를 이용한 3차원 유한요소해석을 수행하였다. 다양한 수치 예를 제시하여 링 보강 주름 원통쉘의 동특성을 이해할 수 있도록 하였다.
2. 이론 전개
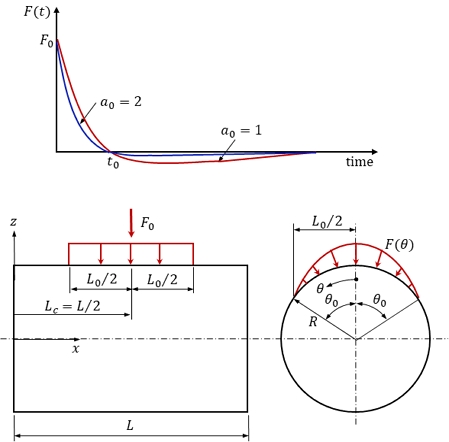
Fig. 1에서처럼 길이 방향 주름을 갖고 링으로 쉘의 내부에 보강된 원통쉘이 외부 충격하중을 받는다. 그림에서 L, R은 원통쉘의 길이 및 평균 반지름이다. 고려된 주름 형상은 사다리꼴로 단위 주름 요소에 대해 주름각을 α, 반 주기 길이를 c, 진폭을 f, 펼친 길이를 2l, 두께를 tc로 표기하였다.
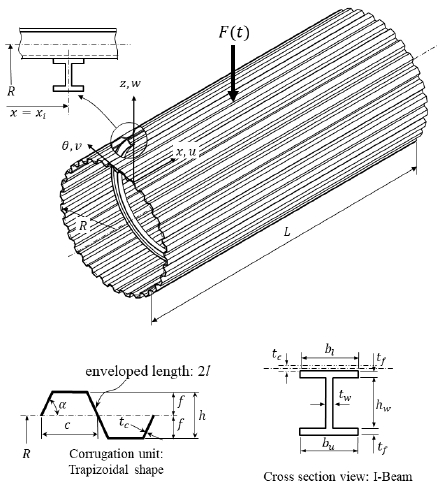
Longitudinal corrugated cylindrical shell with internal ring stiffeners, a corrugation unit and section view of stiffener
주름각이 커짐에 따라 주름 형상은 삼각형에서 사다리꼴로 전환된 후 사각형(α=90°)으로 변한다. 또한 링 보강재는 x 방향으로 등간격으로 쉘의 내부에 위치하며, I형 단면을 갖는 열린 단면 보가 고려되었다. 플랜지 폭을 bi, bu, 웨브의 높이를 hw, 플랜지 및 웨브의 두께를 각각 tf, tw로 나타냈다.
본 연구에서 주름 원통쉘을 균일한 두께 h(=2f)를 갖는 직교 이방성 재료로 등가시켜 해석에 이용하였다. 등가 직교 이방성 원통쉘에 대해 Love의 쉘이론을 적용하였으며, 이로부터 각 방향에 대한 변형률 및 곡률은 다음과 같이 표현된다.
| (1) |
| (2) |
여기서, u, v 및 w는 x, y 및 z 방향 변위이다. 또한 ( , )는 다음에 나타나는 첨자에 대한 미분을 의미한다.
등가 직교 이방성 원통쉘의 변형 및 운동에너지는 다음과 같다.
| (3) |
| (4) |
여기서, 는 원통쉘을 직교 이방성 셸로 등가시켜 얻은 등가 신장 및 굽힘 강성계수이다.3) ρ는 쉘 재료의 밀도, ( ∙ )는 시간에 대한 미분을 나타낸다.
보 형태의 보강재에 대해 등가 셸의 중립면으로부터 수직 방향 거리 z에서의 변위장은 다음과 같이 된다.
| (5) |
보강재의 원주 방향 수직 및 비틀림 변형률을 다음과 같이 쓸 수 있다.
| (6) |
한편, x = xi에 위치하는 i번째 보강재의 변형에너지 및 운동에너지는 다음과 같다.
| (7) |
| (8) |
여기서, δ는 디랙 델타(Dirac delta) 함수로 변형 형상 등에서 보강재의 위치에 따른 영향을 나타내기 위해 사용되었다. EA, GJ는 보강재의 신장 및 비틀림 강성이다. dVr은 보강재의 미소 체적이다.
쉘의 양단에서 다음과 같은 단순 지지 경계조건을 갖는 원통쉘을 고려하였다.
| (9) |
위의 경계조건을 만족하는 원통쉘의 변위식을 다음과 같이 급수 형태로 가정하였다.
| (10) |
여기서, Umn, Vmn, Wmn는 고유 모드, 계수 αm = mπ/L이고, m, n은 모드 수, ηmn (t)는 모드 기여도 인자이다.
Fig. 2에서처럼 원통쉘의 외부에 짧은 시간 동안 쉘의 중앙 (x = L/2, θ0 = 0°)에 집중하중 또는 분포하중 형태로 작용하는 충격하중을 고려하였다. 분포하중의 크기는 그림과 같이 쉘의 길이 방향으로는 일정하며, 원주 방향으로는 함수적으로 변한다고 가정하였다.
| (11) |
여기서, F0는 하중 최대 크기, a0는 시간에 따른 파장 감소 계수(2 이상)이며, t0는 양의 하중이 가해지는 하중 지속 시간으로 이후에는 a0에 따라 크기가 달라지는 음의 하중이 작용한다. 분포하중의 경우 쉘의 길이 방향 전체에 걸쳐 작용하며, θ0는 압력의 원주 방향 분포 각도로 90°만 고려하였다. 따라서 하중 분포 면적은 L0(=L) × θ0(=90°)가 된다. 작용 하중을 급수 형태로 표현하면 다음과 같다.
| (12) |
여기서, Fmn은 하중 분포 상태에 따라 결정되며, 시간에 대한 함수 fmn (t)은 다음과 같이 Duhamel 적분 형태로 표현할 수 있다.
| (13) |
여기서, ωmn은 고려된 원통쉘의 (m, n)모드에서의 고유 각진동수이다.
외부 하중에 의해 원통쉘이 한 일은 다음과 같다.
| (14) |
충격하중에 의해 보강된 원통쉘에 저장된 총 포텐셜 에너지는 아래와 같다.
| (15) |
동하중에 대한 구조물의 응답을 구하기 위해 식 (15)에 Rayleigh-Ritz 정리를 적용한 후 변분을 취하면 다음과 같은 운동방정식을 얻을 수 있다.
| (16) |
여기서, K, M은 강성 및 질량행렬, Q는 하중 벡터, d는 모달 행렬이다.
식 (16)은 다음과 같이 간단히 정리할 수 있다.
| (17) |
따라서 식 (17)의 해는 다음과 같다.
| (18) |
이 결과, 식을 각 방향 변위식 (10)에 대입하면 구하고자 하는 응답을 얻게 된다. 제안된 방법으로 동적 응답 등을 구하기 위해 Mathematia를 이용하여 프로그램을 작성하였다.
3. 수치 결과 및 토의
동적 응답에 대한 제안된 해석 방법의 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하였다. 유한요소해석에서는 진동해석과 과도응답 해석을 모두 수행하였다. 유한요소해석에서 주름 쉘 및 링 보강재는 SHELL281 요소를 이용하여 모델링하였다. 고려된 원통쉘의 크기, 주름 특성 및 보강재의 크기는 다음과 같다. 이때 쉘은 2개의 링 보강재가 등간격으로 쉘의 안쪽에 보강된다. 이들 기하 자료는 특별한 언급이 없는 한 앞으로의 모든 수치 예에 사용된다.
여기서, Nc는 주름수이다. 충격하중은 쉘의 중앙에 집중하중(F0 = 10kN)을 받으며, t0 = 2, 3ms, 파장 감소 계수 a0 = 2로 모든 예제에 적용된다.
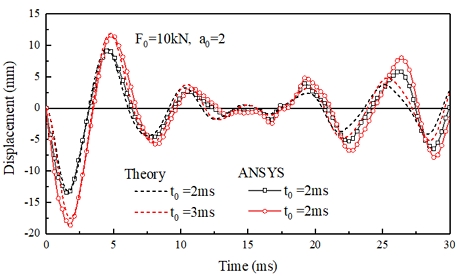
고려된 모델에 대해 과도응답에 가장 큰 영향을 주는 저차 모드에서의 고유진동수 및 진동모드를 Table 1에 제시하였다. 표에 나타난 것처럼 두 결과 간의 차이는 매우 작은 것을 확인할 수 있다. 또한 충격하중을 받는 쉘에 대한 하중 작용점인 중앙점에서의 처짐에 대해 유한요소 및 이론해석 결과를 Fig. 3에 제시하였다. 고려된 조건에 대해 최대 처짐은 하중이 가해지는 강제 진동 구간인 첫 번째 정점에서 발생되며, 후속 자유 진동 구간에서의 거동은 이보다 작은 진폭으로 진동을 한다. 최대 처짐에 대해 두 해석 결과 간의 차이는 하중 지속 시간이 짧은 경우에는 거의 나타나지 않으나, 지속 시간이 비교적 긴 t0 = 3ms인 경우 약 6% 정도 나타난다. 전반적으로 두 결과가 잘 일치하는 것을 볼 수 있다. 두 해석 결과의 응답 주기가 6~7 ms로 응답 주기에 가장 큰 영향을 미치는 저차 고유진동수 중에서 축 방향 모드 m = 3인 2, 3차 고유진동수의 주기가 약 7 ms로 이들의 저차 진동수가 동적 응답에 영향을 준 것으로 판단된다. 참고로 보강재가 2개인 쉘의 축 방향 변형 형상은 Fig. 5에서처럼 m = 3의 모드를 하고 있다.
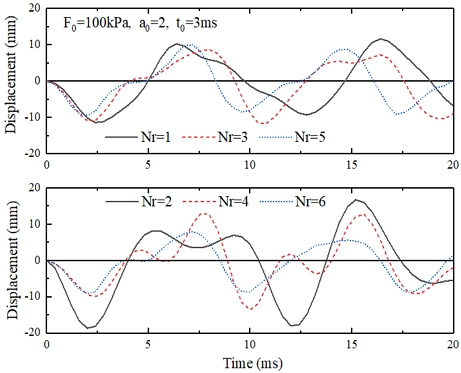
Fig. 4는 분포하중(F0 = 100kPa, t0 = 3ms)을 받는 링 보강 주름 원통쉘에 대해 링 보강재 수에 따른 쉘의 중앙점에서의 시간 응답이다. 쉘의 전면 전체에 걸쳐 분포하중을 받는 경우, 시간에 따른 응답 경향이 Fig. 3의 집중하중을 받는 경우와 다소 다른 것을 볼 수 있다. 집중하중의 경우, 하중이 가해지는 강제 진동 구간에서 최대 처짐이 발생된 후 빠르게 감소한 후 다시 자유 진동 구간에서 큰 처짐이 나타난다. 그러나 분포하중을 받을 경우에는 처짐 감소 구간이 나타나지 않는 것을 볼 수 있다. 홀수 개로 보강되었을 때 중앙점에서의 처짐변화는 중앙에 보강재가 있기 때문에 짝수 개로 보강된 경우에 비해 그다지 크지 않지만, 보강재가 5개 이상이 되면 유사한 거동을 한다. 전반적으로 보강재 수가 증가함에 따라 처짐이 감소하는 것을 볼 수 있다. 그러나 보강재 수가 어느 이상이 되면 처짐변화는 거의 없다. 이처럼 보강재 수에 따라 중앙점에서의 처짐이 급격히 감소한 후 일정값으로 수렴이 되기 때문에 보강 구조물 설계를 위해서는 보강재 수에 따른 거동을 검토하여 설계에 적용하여야 할 것이다.
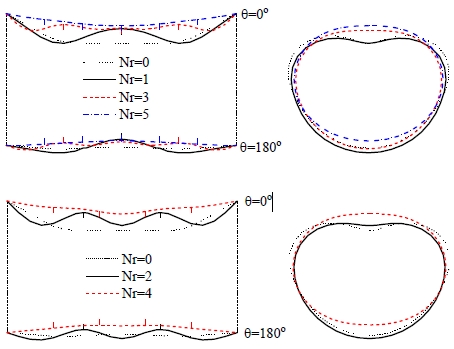
Fig. 5는 Fig. 4의 결과에 대해 첫 번째 강제 진동 구간의 최대 처짐이 발생하는 시간에서 길이방향 및 원주 방향에 대한 변형 형상을 나타낸 것이다. 길이 방향에 대한 처짐은 θ = 0° 및 180°에서의 값이다. 원주 방향 처짐 형상은 최대 처짐이 발생되는 길이 방향 지점에서의 값으로, 최대 처짐이 발생되는 지점은 홀수 개로 보강된 경우에는 경계 단과 보강재 사이이다. 그러나 보강재 수를 더 증가시키면 보강재 사이의 거리가 짧아져 최대 처짐은 중앙점에서 발생된다. 짝수 개로 보강된 경우에는 중앙에서 최대 처짐이 발생된다. 그림에서처럼 보강재 수가 2개인 경우에는 최대 처짐이 비보강쉘의 경우와 거의 같아 보강 효과를 얻을 수 없다. 따라서 최소 2개 이상이 되어야 처짐에 대해 보강 효과를 얻을 수 있다. 보강함으로써 비보강 주름 원통쉘의 처짐 대비 Nr = 6의 보강 원통쉘의 경우 약 60%의 처짐 감소를 얻을 수 있다(Fig. 4 참조).
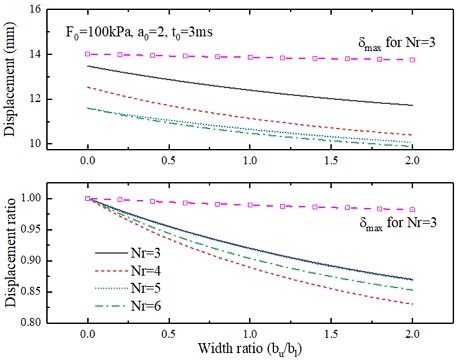
앞의 예제와 같은 분포하중을 받는 원통쉘에 대해 보강재의 상단 플랜지 폭에 따른 영향을 Fig. 6에 제시하였다. 여기서 bl = 5tc, hw/tc = 20로 고정하였다. 전반적으로 중앙에서 최대 처짐이 발생되기 때문에 중앙점에서의 처짐을 제시하였다(Fig. 5 참조). 그러나 Nr=3인 경우에는 Fig. 5에서처럼 L/4 부근에서 최대 처짐이 발생되기 때문에 최대 처짐을 참고로 제시하였다. 또한 상단 플랜지가 있는 보강 쉘의 처짐을 상단 플랜지가 없는 쉘의 처짐으로 나눈 처짐 비를 제시하였다. 그림에서처럼 상단 플랜지 폭이 증가함에 따라 처짐은 감소한다. 홀수 개로 보강된 경우에는 보강재 수에 관계없이 처짐이 거의 같은 비로 감소를 한다. 그러나 짝수 개로 보강될 경우에는 보강재가 적을 경우보다 많이 감소하는 것을 볼 수 있다. 이와 같은 이유는 보강재가 많을수록 보강재 수에 따라 이미 큰 보강 효과를 얻을 수 있기 때문에 폭에 따른 영향이 적게 작용한 결과이다.
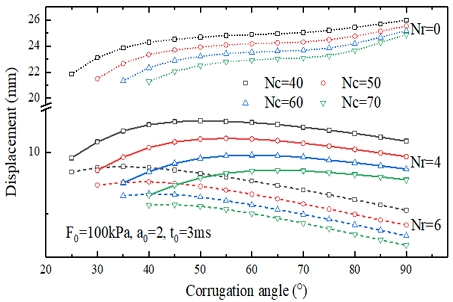
분포하중을 받는 링 보강 주름 원통쉘에 대해과도 응답 중 강제 진동 구간에서의 최대 처짐을 주름각에 따라 Fig. 7에 제시하였다. 비교를 위해 비보강쉘에 대한 결과도 제시하였다. 주름각이 커짐에 따라 주름쉘의 원주 방향 등가 강성계수는 감소하고, 길이 방향 강성계수는 증가한다.4) 이에 따라 비보강쉘의 경우, 원주 방향 강성계수의 영향이 커 처짐이 증가하는 거동을 한다. 보강쉘의 경우, 고려한 모든 주름수에 대해 초기 주름각에서 처짐이 비 보강쉘처럼 증가를 하다가 정점을 이룬 후 감소한다. 보강 재수가 많을수록 처짐이 증가하는 거동은 일찍 사라진다. 또한 보강 재수가 많은 경우, 주름각의 영향이 더 크게 작용하는 것을 볼 수 있다. 이는 보강재 간의 쉘부분 길이가 짧아져 길이 방향 강성의 영향이 처짐에 좀 더 크게 작용한 것으로 판단된다. 또한 그림에서 주름수에 따른 영향도 확인할 수 있다. 그림에서처럼 주름수가 많아질수록 처짐은 많이 감소한다. 특히 주름각이 작은 경우, 그 영향은 더욱 크게 나타난다. 위의 결과 중에서 링 보강을 함으로써 약 66%까지 처짐을 줄일 수 있다.
4. 결 론
I형 단면 보의 링으로 보강된 주름 원통쉘에 대해 충격하중에 의한 동적 응답 특성을 알아보기 위해 이론해석을 수행하였다. 해의 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하여 두 결과를 비교하였다. 이를 통해 복잡한 유한요소 모델링을 하지 않아도 제안된 이론해석 방법이 링 보강 주름 원통쉘의 동적 응답을 적절히 예측할 수 있음을 보였다.
충격하중을 받는 원통쉘에 대해 보강재 수, 플랜지 폭의 크기 및 주름 특성이 동적 응답에 미치는 영향을 알아보았다. 보강재 수가 증가함에 따라 처짐은 작아지지만, 어느 이상이 되면 처짐은 일정한 값으로 접근한다. 플랜지 폭이 넓어질수록 처짐은 감소하며, 그 영향은 보강재 수가 적을수록 커진다. 주름각이 증가함에 따라 비보강 쉘의 경우 최대 처짐은 증가를 한다. 적은 수의 링으로 보강된 쉘의 경우에는 초기에는 최대 처짐이 증가를 하다가 정점을 이룬 후 감소하는 거동을 한다. 그러나 많은 링으로 보강된 경우에는 감소하는 경향을 보인다. 주름수가 많아질수록 처짐은 감소하며, 작은 주름각에서 그 영향은 크게 나타난다. 또한 본 해석 방법을 통해 변형 형상을 예측할 수 있었으며, 특히 보강재 사이에 나타나는 국부 변형 형상까지도 예측할 수 있었다.
Author contributions
Conceptualization, Data curation, Formal analysis, Methodology, Validation, Writing-original draft, Writing-review & editing.
References
-
I. G. Emel'yanov and D. A. Ogorelkov, 2023, “Fatigue of a cylindrical shell lying on a rigid bed”, Procedia Structural Integrity, 50, 57-64. (10.1016/j.prostr.2023.10.022)
[https://doi.org/10.1016/j.prostr.2023.10.022]

-
C. T. F. Ross, A. P. F. Little, P. Kӧster and G. Tewkesbury, 2006, “Vibration of a Thin-walled Carbon Fibre Corrugated Circular Cylinder under External Water Pressure”, Thin-walled Structures, 44(5), 542-553.
[https://doi.org/10.1016/j.tws.2006.04.011]

-
T. G. Ghazijahani, H. Jiao and D. Holloway, 2015, “Longitudinally Stiffened Corrugated Cylindrical Shells under Uniform External Pressure”, Journal of Constructional Steel Research, 110, 191-199.
[https://doi.org/10.1016/j.jcsr.2015.02.016]

-
Y. W. Kim, 2016, “Vibration Analysis of Longitudinally Corrugated Cylindrical Shells”, Transactions of the Korean Society for Noise and Vibration Engineering, 26(7), 851-856.
[https://doi.org/10.5050/KSNVE.2016.26.7.851]

-
S. E. Alkhatib, F. Tarlochan, A. Hashem and S. Sassi, 2018, “Collapse behavior of thin-walled corrugated tapered tubes under oblique impact”, Thin-Walled Structures, 122, 510-528.
[https://doi.org/10.1016/j.tws.2017.10.044]

-
Y. Liu, W. Hu, R. Zhu, B. Safaei, Z. Qin and F. Chu, 2022, “Dynamic Responses of Corrugated Cylindrical Shells Subjected to Nonlinear Low-velocity Impact”, Aerospace Science and Technology, 121, 107321.
[https://doi.org/10.1016/j.ast.2021.107321]

-
P. Iwicki, K. Rejowski and J. Tejchman, 2015, “Stability of Cylindrical Steel Silos Composed of Corrugated Sheets and Columns Based on Fe Analyses versus Eurocode 3 Approach”, Engineering Failure Analysis, 57, 444-469.
[https://doi.org/10.1016/j.engfailanal.2015.08.017]

-
S. Maleki and A. M. Mehretehran, 2018, “3D Wind Buckling Analysis of Long Steel Corrugated Silos with Vertical Stiffeners”, Engineering Failure Analysis, 90, 156-167.
[https://doi.org/10.1016/j.engfailanal.2018.03.031]

-
P. Hajko, J. Tejchman and M. Wójcik, 2018, “Investigations of Local/Global Buckling of Cylindrical Metal Silos with Corrugated Sheets and Open-sectional Column Profiles”, Thin-Walled Structures, 123, 341-350.
[https://doi.org/10.1016/j.tws.2017.11.037]

-
P. Iwicki, K. Rejowski and J. Tejchman, 2019, “Determination of Buckling Strength of Silos Composed of Corrugated Walls and Thin-walled Columns using Simplified Wall Segment Models”, Thin-Walled Structures, 135, 414-436.
[https://doi.org/10.1016/j.tws.2018.11.018]

- R. C. Davis, 1982, “Buckling Test of A 3-Meter-Diameter Corrugated Graphite-epoxy Ring-stiffened Cylinder”, NASA Technical Paper 2032.