풍력발전기용 3열 롤러 피치 베어링의 롤러 프로파일에 따른 응력 평가

1. 서 론

현재 지구 온난화의 문제를 줄이고자 넷제로(Net Zero), 저탄소를 위한 재생에너지원으로서 풍력 발전기 개발과 보급이 확대되고 있는 추세이다. 특히 석탄화력 발전의 탄소 발생의 주범인 에너지원에 대한 보급 및 사용상의 경제적 우위를 확보하고자 대형 풍력발전기의 개발과 보급이 합리적 대안으로 제시되고 있다. 이러한 대형 터빈의 개발은 로터 직경의 증대로 이어지고, 이것은 블레이드의 길이뿐 아니라 허브 사이즈와 피치 베어링의 사이즈 증대 및 타입 변경을 수반한다.

기존 중소형 풍력발전기에 적용되는 단열 또는 복렬의 볼 베어링으로는 터빈 용량 증가에 따라 증가된 베어링의 정적 및 동적 하중을 견디기 어렵기 때문에 최근 대형 풍력발전기에는 3열 롤러 베어링이 적용되고 있는 추세이다.

풍력발전기용 피치베어링은 선회 베어링으로, 기계장치의 회전축에 장착되어 외부 하중을 지지하는 동시에 상부체를 회전시키는 구름 베어링의 한 종류이다. 단 방향의 하중을 지지하는 일반 구름 베어링과 달리, 선회 베어링은 축 방향, 반경 방향 및 굽힘 모멘트의 복합 하중을 지지한다. 이러한 하중 수용 특성 덕분에 굴삭기, 타워 크레인 등의 여러 산업 장비 및 본 연구 대상인 풍력 발전기용 피치 베어링에 널리 사용된다. 블레이드 베어링이라고 부르기도 하는 피치 베어링은 로터 허브와 블레이드를 연결해주는 선회 베어링으로 매우 낮은 회전 속도로 좌/우로 진자운동(Oscillation movement)을 가능하게 하여 발전 효율을 높이거나, 정격 풍속 이상에서 실속제어에 의해 정지되어 하중을 지지한다. 이처럼 풍력발전기용 피치 베어링은 풍향과 풍속에 따른 블레이드의 환경적 요인으로 인해 매우 가혹한 동적 복합 하중을 받는다.

터빈의 대형화 추세에 피치베어링의 인접 구조물인 로터 허브와 블레이드 크기가 증가함에 따라, 피치베어링은 더 높은 구조적 강성을 가지도록 설계되어야 한다. 롤러 베어링은 롤러의 기하학적 특성과 롤러와 궤도면 간의 접촉은 롤러 끝단에서 과다한 응력 집중(Edge loading)을 발생시킬 수 있으며, 영구변형을 일으키는 손상 또는 궤도면에 Pitting과 Spalling 등과 같은 조기 피로 파손 등을 일으킬 수 있다.

본 연구에서는 이러한 엣지 로딩 문제를 최소화하기 위해, 인접 구조물인 허브와 블레이드의 비대칭 강성 분포와 변형이 3열 롤러 피치 베어링의 하중 분포에 미치는 영향을 분석하여 롤러의 엣지 로딩을 피하기 위한 최적의 롤러 프로파일을 도출하였다.

본 연구와 관련된 대표적인 선행연구로, Lundberg(1939)는 롤러의 축방향 응력분포를 균일하게 분포시킬 수 있는 로그함수 형태의 로그함수 형태의 대수 분포(Logarithmic profile)를 제안하였다.¹⁾ John과 Gohar(1981)는 Lundberg가 제안한 프로파일을 보다 실용적으로 개선하여, 수정된 대수함수 형태의 프로파일을 제안한 바 있다. 수정된 로그함수 형태의 대수 분포을 제안하였다.²⁾ 하지만 이 제안된 프로파일은 오정렬 시 최대 압축응력이 과소평가되는 사례가 있어, 최대하중 조건에서 최적화된 롤러 응력분포 프로파일을 도출하는데 한계가 있다. 또한 고정된 형상을 가지고 있기 때문에 다양한 설계요구 사항을 충족하기가 어렵다. 이에 따라 Fujiwara와 Kawase (2009)는 앞서 연구한 Profile을 발전시켜, 새로운 설계 변수들을 도입 하여 설계 유연성을 확보하고 실제 적용에 있어 최적화의 타당성을 검증하였다.³⁾ Fujikawa와 Yamauchi (2010)는 최적화된 logarithmic profile을 활용하여 롤러에 대한 공차 설계 방안을 제안하였다.⁴⁾

최근에는 구조해석을 활용하여 응력분포를 계산하여 개선하려는 연구도 활발히 진행되고 있다. Kang and Heo(2020)는 볼 베어링에 대해 비선형 스프링 모델을 바탕으로 베어링 구조에 따른 접촉부 응력 계산하였다.⁵⁾ Kim과 Moon(2012)은 풍력발전기의 볼 베어링에 대한 피로수명 계산하기 위해서 복합 하중 상태에서 하중 분배를 계산하였다.⁶⁾

Wang and He(2017)은 풍력발전기용 대형 3열 롤러 베어링의 하중 분포를 계산하기 위하여 비선형스프링 모델을 사용하여 솔리드 모델과 동등한 결과를 보여 줄 수 있는 해석 방안을 제시하였다.⁷⁾

Stammler와 Baust(2018)는 인접구조물인 로터 허브와 블레이드의 비대칭 강성을 고려한 3열 롤러피치 베어링의 하중 분포 연구를 수행하였다.⁸⁾ 이 연구 내용은 3열 롤러 피치 베어링의 하중분포에 대하여 인접 구조물의 비대칭 강성과 변형에 많은 영향을 받는 것을 보여 주었으나, 베어링 조기파손을 막기 위한 롤러의 응력 프로파일에 관한 최적화 연구는 수행되지 않았다.

따라서 본 연구에서는 선행연구에서 찾아보기 어려운 3열 롤러 피치 베어링의 인접 구조물인 허브와 블레이드의 강성과 변형을 고려하여 베어링 하중 분포를 계산하고, 최대 하중을 받는 롤러의 엣지 로딩을 피하기 위한 롤러 프로파일 최적화를 수행하였다.

2. 연구내용 및 방법

2.1 3열 롤러 피치 베어링의 구조

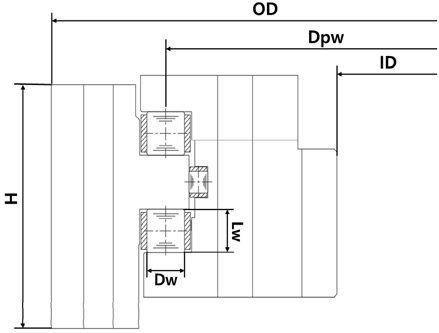
3열 롤러 피치 베어링은 Fig. 1과 같이 외내륜의 궤도륜과 축 방향 하중과 모멘트 방향의 하중을 지지하는 Axial roller가 상하로 배열되고 반경방향의 하중지지 및 회전구동하기 위한 Radial roller가 중앙에 배열되어, 총 3열의 롤러로 구성되어 있다.

Fig. 1

The geometry of 3 row roller bearing

베어링 링파트는 42CrMo4 재질로 궤도면과 기어에는 고주파 열처리가 되며, 전동체는 100Cr6 재질의 롤러로 구성된다.

Table 1과 2는 해당 베어링에 대한 주요한 치수 및 재료에 대해 각각 정리하였다.

Table 1

The dimension of roller and bearing

Table 2

Material parameter for roller and ring

2.2 베어링 해석 모델

피치 베어링의 사이즈가 커짐에 따라 요소부품 수도 증가하며, 수백 개의 롤러와 궤도면 간의 접촉 경계조건의 수가 비례하여 증가하게 되므로 해석에 많은 시간과 비용이 소모된다.

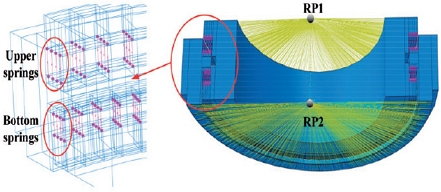
Wang과 He가 제시한 비선형 스프링모델⁷⁾들을 사용한 결과에서는 솔리드 롤러 모델을 활용한 궤도면과의 접촉응력 계산의 결과가 동일하다는 것을 보여 준 바 있어, 본 연구에서는 계산 시간적으로 유리한 스프링 모델을 활용하였다. Fig. 2는 Wang과 He가 제시한 비선형 스프링 모델의 예시이며, 롤러 접촉 경계조건을 비선형 스프링 모델로 Fig. 3과 같이 정의하였다.

Fig. 2

Wang and He's nonlinear spring model for rollers for 3 row roller bearing

Fig. 3

Bearing FE model including nonlinear spring for rollers

본 연구에서 고려된 로터 허브와 블레이드 그리고 3열 롤러 피치 베어링의 조립체의 복잡성을 고려하여 Fig. 3과 같이 스프링 조건을 모델링하였다. 스프링 개수를 조밀하게 정의할수록 계산의 정확도는 향상될 수 있으나 해석에 소요되는 시간 경제성을 고려하여 형상의 복잡도를 잘 반영하고 솔리드 롤러 모델과 동일한 수준의 하중 분포를 보일 수 있는 스프링 개수 선정하였다. 고려된 스프링은 롤러 요소당 4개로 정의하였으며, 1열당 250여 개 세트로 정의하였다.

2.3 Pitch 베어링 해석 방법

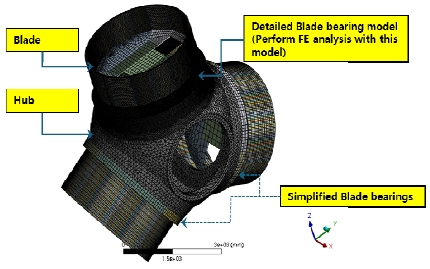
3열 롤러 피치 베어링의 롤러 프로파일 최적 설계하기 위해 Fig. 4와 같이 3개의 피치 베어링과 3개의 블레이드 그리고 허브로 구성하였다. 본 연구에서는 3개의 피치 베어링 중 1개 베어링에 대하여 스프링 모델이 고려된 상세 해석을 수행, 나머지 2개 파트는 구속조건을 부여하여 접근하였다.

Fig. 4

FE model of pitch bearing and companion structure (Hub and blade) in this study

Fig. 5와 같이 인접 구조물과 베어링 간의 인터페이스 면은 Friction contact 조건을 부여하였으며, 허브 측 내륜은 블레이드와 접촉, 예압을 고려한 볼트 체결을 고려한 구속조건을 부여하였다. 나머지 2개의 베어링과 블레이드는 전체 로터 허브의 강성과 변형을 고려하기 위해 단순화하여 모델링하였으며, 조립체 모델에 Bonded 조건으로 구속시켰다. 마찰계수는 0.2로 설정하였으며, Steel –Steel(dry) 마찰계수 0.1 ~ 0.3의 중간값을 활용하였다.

Fig. 5

FE model of pre-tensioned bolts for bearing connection between hub and blade

2.4 피치 베어링 좌표 시스템

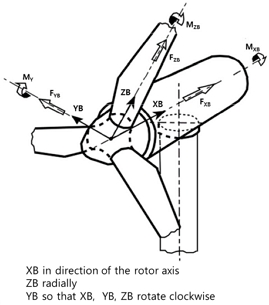
피치 베어링은 블레이드에 작용하는 바람과 블레이드의 피치각 조절 등 다양한 이유에 의하여 복합적인 하중을 받게 되며, 복합하중은 축 방향, 반경 방향, 모멘트 하중을 받는다. Fig. 6에 피치 베어링의 좌표 시스템을 나타내었으며, XB는 로터의 축 방향, ZB와 YB는 반경 방향을 나타낸다.

Fig. 6

Coordinate system of blade

2.5 하중 조건

풍력터빈의 Coordinate system은 Fig. 6을 기준으로 정리할 수 있다. Table. 3의 하중 조건은 풍력발전기 제조사로부터 받은 자료이며, Extreme Load는 피치 베어링이 받을 수 있는 최대 하중을 나타내고 Fatigue Load는 정상 가동(발전) 상태에서 발생하는 하중이다. Case 1은 해당 피치 베어링이 받을 수 있는 최대 하중 조건이며, Case 2와 Case 3는 정상 가동할 때 발생하는 가장 큰 하중과 가장 작은 하중이다. 여기서, 2번의 피로하중 사이클은 1만 사이클, 3번의 피로하중 사이클은 1만 5천 사이클이다.

Table 3

Load cases for 3 row roller pitch bearing

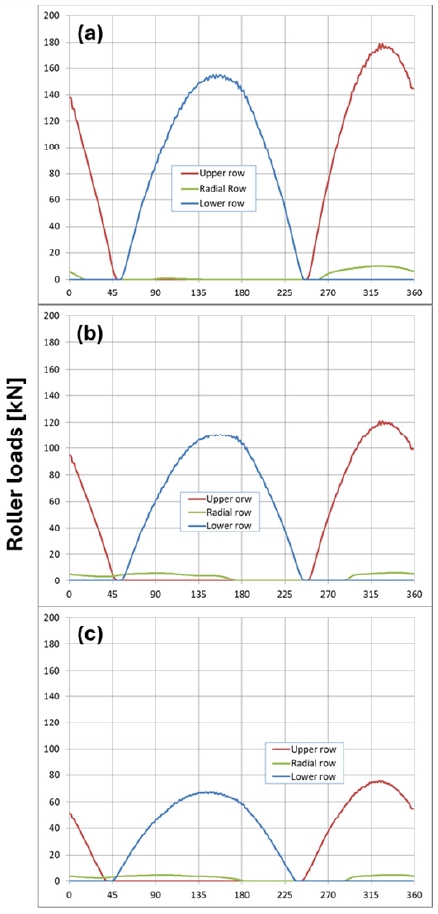
2.6 하중 분포

3열 롤러 피치 베어링의 롤러 프로파일을 최적화하기 위해서는 우선 외력이 가해질 때의 베어링 하중 분포를 계산하여야 한다.⁹⁾ 유한요소 해석을 통해서 인접 구조물의 강성을 고려한 베어링의 하중 분포 및 최대 롤러 하중을 계산한 결과는 Fig. 7과 같다. 3열 롤러 피치 베어링의 각 열에 대한 하중 분포를 나타내며, Table 4는 유한요소 해석을 통해 얻은 최대 롤러 하중 값들을 정리하였다.

Fig. 7

Roller load distribution under Load cases. (a) Case 1, (b) Case 2, and (c) Case 3.

Table 4

Max. loads results for design cases

2.7 롤러 엣지 로딩 분석

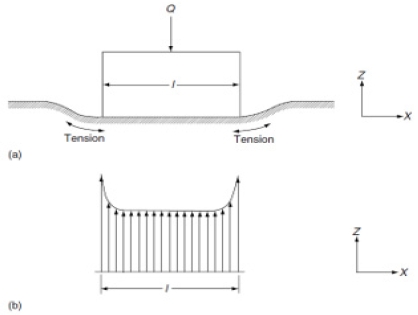
엣지 로딩은 원통형 롤러에 하중이 가해질 때, 롤러가 구르는 접촉면 끝단의 응력이 롤러의 중앙쪽보다 높은 응력집중 현상을 가리킨다. 이러한 엣지 로딩은 아래 Fig. 9로 도식화하여 설명할 수 있다.¹⁰⁾ Fig. 9(a)는 원통형 롤러에 하중이 가해지면, 궤도면의 탄성변형으로 인해 함몰이 발생되고 롤러 끝단 부근의 궤도면에 인장력이 발생되면서 Fig. 9(b)와 같이 롤러 끝단에서 하중이 집중되는 것을 보여 준다. 이러한 원통형 롤러 베어링은 엣지 로딩에 의한 물리적 파손과 변형이 발생하지 않도록 롤러 프로파일을 최적화하여 설계할 필요가 있다.

Fig. 8

Line contact : (a) Interface of roller-raceway, (b) Stress distribution of the contact line

Fig. 9

Design parameter for logarithmic crown profile

롤러 끝단의 엣지 로딩을 피하기 위하여 Lundberg에 의해 처음 고안된 Logarithmic profile의 크라운 롤러는 이후 여러 연구자들을 통해 거듭 수정 및 보완되었다. 본 연구에서는 Fujiwara와 Kawase et al.이 제시한 Logarithmic profile의 최적 방안을 기초로 하여 엣지 로딩발생 여부를 파악하고자 한다. 그들이 제시한 최적화 방안은 롤러의 원통면에 적용되는 크라운 길이를 설정하는 K2, 크라운 드랍을 결정하는 Zm 그리고 크라운 곡률을 정하는 K1의 세 가지 설계변수를 이용하여 최적화하는 방법이다. 이러한 프로파일은 식 (3)에 의해 설명이 가능하다.

$\[ z\left(y\right)=Aln\frac{1}{1-\left\{1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{z_m}{A}\right)\right\}{\left(\frac{y-\frac{L_{we}}{2}}{k_2\frac{L_{we}}{2}}+1\right)}^2} \]$

(3)

$\[ A=\frac{2K_{1}Q}{\pi L_{we}{E}^{\text{'}}} \]$

(4)

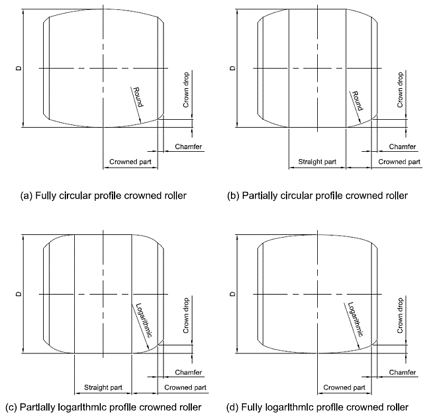
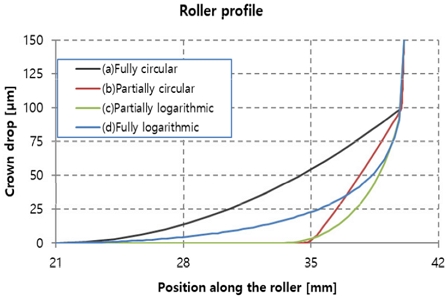
Fig. 10과 같이 동일한 크라운 드랍을 기준으로 4가지 형태의 크라운 프로파일을 가진 롤러를 비교 분석하였다. 롤러의 상세 치수와 크라운 프로파일은 Table 5와 Fig. 11에 도시하였다.

Fig. 10

The types of crowned roller

Table 5

Specification of each crowned roller

Fig. 11

Detail of crown profiles

3. 결과 및 고찰

3.1 롤러 프로파일의 형상에 따른 접촉응력

롤러와 궤도면 접촉으로 발생되는 접촉응력은 풍력발전기용 3열 롤러 피치 베어링의 하중 용량과 수명을 결정짓는 매우 중요한 요소이다. 또한 롤러 엣지부의 응력집중은 베어링의 조기 파손의 주요 원인이어서, 엣지로딩을 피하고 접촉응력을 최소화 하기 위해서는 롤러의 프로파일 선정이 매우 중요하다. 롤러 프로파일에 따른 접촉응력과 엣지 로딩 여부를 파악하기 위하여 베어링 설계 상용 프로그램인 Romax를 이용하여 해석하였다.

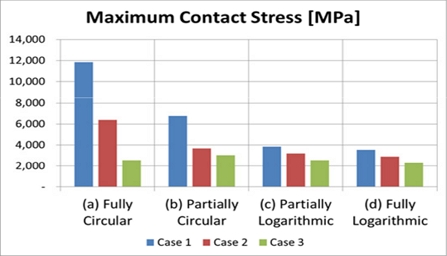
하중 조건과 롤러의 크라운 프로파일 형상에 따른 접촉 응력 결과는 Fig. 12와 Table 6에 제시하였다. Fully Circular Profile Crowned Roller와 Partially Circular Profile Crowned Roller는 롤러 엣지 부위에서 크라운 드롭(crown drop)의 기울기가 완만하여, 엣지 부위에서 접촉이 발생함에 따라 높은 응력집중이 발생하였다. 이러한 응력집중으로 인해 두 경우 모두 ISO 76 규격에서 제시한 롤러 베어링의 최대 허용 접촉 응력인 4,000MPa를 초과하였으며, 각각 11,859MPa 및 6,751MPa으로 사용에 부적합한 것으로 나타났다.

Fig. 12

Maximum contact stress according to roller crown profiles

Table 6

Maximum roller contact stress according to roller profile

반면, Partially Logarithmic Profile Crowned Roller와Fully Logarithmic Profile Crowned Roller의 경우, 롤러 엣지 부위에서 크라운 드롭의 기울기가 충분히 커서 엣지 부위에서의 접촉이 발생하지 않았다. 극한하중 조건(Extreme load)에서도 이들 롤러의 접촉응력은 각각 3,841MPa와 3,528MPa로 ISO 76의 최대 허용값인 4,000MPa를 초과하지 않아 사용에 적합한 것으로 평가되었다. 특히 Fully Logarithmic Profile Crowned Roller는 Partially Logarithmic Profile Crowned Roller와 달리 직선과 곡선의 이행 구간이 없어, 롤러 전체 구간에 걸쳐 응력이 균일하게 분포하며 가장 낮은 접촉응력을 나타냈다.

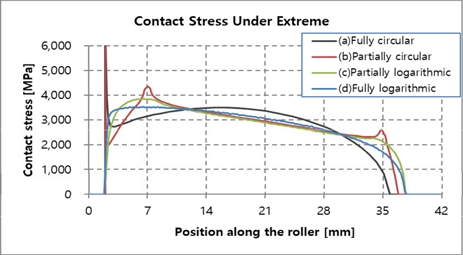
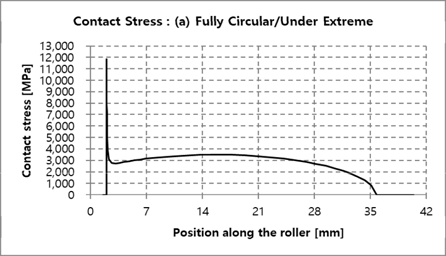
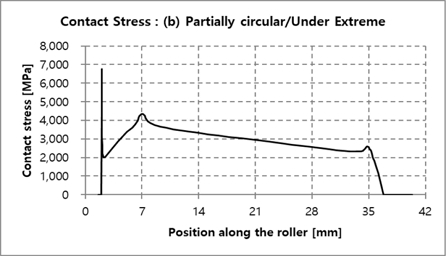
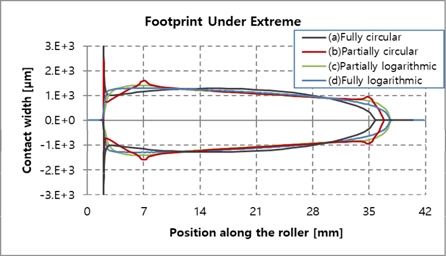
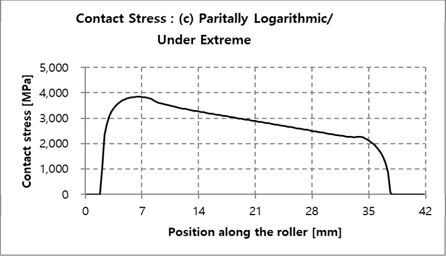
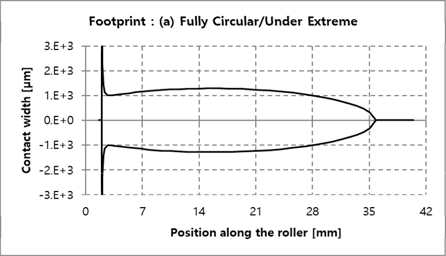
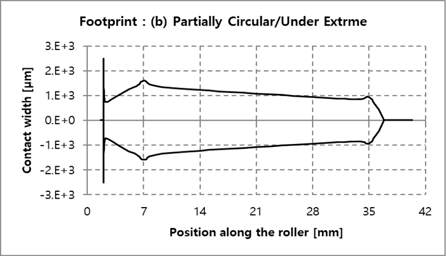
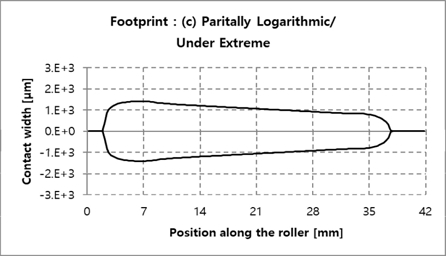
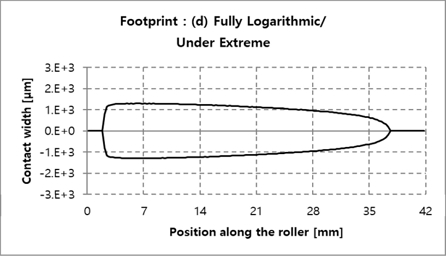
Fig. 13에 롤러 길이 방향에 대한 접촉응력 결과를 비교하였으며, 개별 데이터는 Fig. 14~17에서 확인할 수 있다. Fully logarithmic의 경우에서 가장 낮은 접촉응력을 보였으며, 원인을 분석하기 위해 극한하중 하에서 롤러 접촉 폭을 Fig. 18에 비교하여 나타내었다. 결과에서 알 수 있듯이 Fully logarithmic 롤러 프로파일의 경우, 극한하중 하에서 롤러 접촉 폭이 다른 롤러 프로파일의 경우들보다 비교적 고르게 분포함을 확인할 수 있다. 이는 하중을 고르게 분산시키는데 유리함을 의미하며, 이에 따라 가장 낮은 하중이 얻어짐을 알 수 있다. Fig, 19~22는 Fig. 18의 개별 세부해석 결과를 나타낸다.

Fig. 13

Contact stress distribution for crown profile types of crowned roller

Fig. 14

Contact stress distribution for fully circular profile crowned roller under extreme

Fig. 15

Contact stress distribution for partially circular profile crowned roller under extreme

Fig. 16

Foot print for crown profile types of crowned roller

Fig. 17

Contact stress distribution for partially logarithmic profile crowned roller under extreme

Fig. 18

Foot print for fully circular profile crowned roller under extreme

Fig. 19

Foot print for partially circular profile crowned roller under extreme

Fig. 20

Foot print for partially logarithmic profile crowned roller under Extreme

Fig. 21

Foot print for fully logarithmic profile crowned roller under extreme

4. 결 론

본 연구는 대형 풍력 발전기용 3열 롤러 피치 베어링의 롤러 엣지 로딩으로 인한 조기파손 문제를 피하기 위하여 롤러 프로파일에 따른 접촉응력을 유한요소 해석을 수행하여 다음과 같은 결론을 얻었다.

1) 롤러 크라운 프로파일 형상에 따른 분석 : 4개의 롤러 크라운 프로파일 형상에 대하여 접촉응력 및 롤러 축 방향의 응력분포를 해석하였다. 그 결과 Fujiwara와 Kawase et al.이 제시한 로그함수형태의 크라운 프로파일이 엣지 로딩에 의한 접촉응력을 최소화하는 것으로 나타났다.

2) 최적 설계 검토 : 롤러의 원통면 일부가 아닌 전체 구름면에 로그함수 형태의 크라운 프로파일을 적용하는 것이 접촉응력과 엣지 로딩 문제를 피하기 위한 최적 설계임을 확인하였다.

향후 본 연구 결과를 바탕으로 3열 롤러 피치 베어링의 수명 평가와 관련된 롤러 프로파일의 최적화 설계 및 연구를 진행할 예정이다.

Acknowledgments

이 논문은 2021년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임(과제번호 20213000000050, 과제명 15MW급 풍력터빈용 피치&요 베어링(또는 요링) 국산화 개발 기술).

References

• G. Lundberg, 1939, “Elastic Contact Between Two Semi-Infinite Bodies”, Forschung auf den Gebiete Des Ingenieurwesen, 5, 201-211. [https://doi.org/10.1007/BF02584950]
• P. M. Johns and R. Gohar, 1981, “Roller bearings under radial and eccentric loads”, Tribology Inter National, 14, 131-136. [https://doi.org/10.1016/0301-679X(81)90058-X]
• H. Fujiwara, T. Kobayashi, T. Kawase and K. Yamauchi, 2010, “Optimized logarithmic roller crowning design of cylindrical roller bearings and its experimental demonstration”, Tribology Transaction, 53(6), 909-916. [https://doi.org/10.1080/10402004.2010.510619]
• H. Fujiwara and K. Yamauchi, 2010, “Tolerance Design of Logarithmic Roller Profiles in Cylindrical Roller Bearings”, ournal of Advanced Mechanical Design Systems and Manufacturing, 4(4), 728-738. [https://doi.org/10.1299/jamdsm.4.728]
• J. H. Kang, S. J. Heo, J. H. Yu and H. W. Lee, 2020, “Structural Analysis of Slewing bearings for Wind Turbines”, International Journal of Mechanical engineering and technology, 11(11), 6-15. [https://doi.org/10.34218/IJMET.11.11.2020.002]
• Y. J. Kim, S. M. Moon and Y. J. Cho, 2013, “Load distribution, Contact and Fatigue Life Analysis Pitch Bearing for Wind Turbine”, Journal of the Korean Society of Tribologists & Lubrication Engineer, 29(1), 33-38 [https://doi.org/10.9725/kstle-2013.29.1.033]
• H. Wang, P. He, B. Pang and X. Gao, 2017, “A new computational model of large three-row roller slewing bearings using nonlinear springs”, Journal of Mechanical Engineering Science, 231(20), 3831-3839. [https://doi.org/10.1177/0954406217704223]
• M. Stammler, S. Baust, A. Reuter and G. Poll, 2018, “Load distribution in a roller-type rotor blade bearing”, Journal of Physics: Conference Series, 1037(4), 042016. [https://doi.org/10.1088/1742-6596/1037/4/042016]
• T. Harris, J. H. Rumbargar and C. P. Butterfield, 2009, “Wind Turbine Design Guideline DG03 : Yaw and Pitch Rolling Bearing Life”, National Renewable Energy Laboratory. [https://doi.org/10.2172/969722]
• T. Harris and M. N. Kotzalas, 2007, Rolling bearing analysis 5^th edition. [https://doi.org/10.1201/9781482275148]
• International Standard ISO 76, 2006, Rolling Bearings – Static Load rating (3rd ed).
• International Organization for Standardization (ISO), Rolling bearings-Method for calculating the modified reference rating life for universally loaded bearing, ISO/TS 16281, 1^st Ed.