원전 기동운전구간의 고장 감지 방법에 관한 연구

1. 서 론

원자력 발전소는 운전 안전성과 신뢰성 제고를 위해 구성 기기 및 시스템의 실시간 신호 정보를 함께 분석하여 이상징후를 조기에 감지하는 원전 조기경보 시스템을 운영하고 있다.^1,2) 원전 조기경보 시스템은 신호 간의 연관성을 고려하여 과거 정상운전 데이터 패턴을 학습 후 예측하는 방식으로 신호 간의 상관관계가 강한 신호군에서 고장 감지가 정확한 만큼 상관관계가 약한 신호군에도 정확도 및 연산 속도 향상을 위한 기술 확장이 필요하다. 특히 발전소의 계획예방정비 이후 정상출력에 도달하기까지의 기동운전구간에서는 신호 분포가 다양하게 변화하여 정상출력 운전구간의 신호 예측 기법만으로는 고장 감지 성능을 확보하기 어렵다. 이와 관련하여 다양한 최적화 기법들이 연구되고 있으나^3,4) 단일 기법으로 다양한 발전소의 운전 상황을 감시하는데 한계가 있기 때문에 상관관계가 약한 신호군에서도 활용이 가능한 기법을 함께 적용하여 시스템을 보완하는 것이 중요하다.

본 논문에서는 상관관계가 약한 신호군을 대상으로 원전 조기경보 시스템의 예측 정확도를 확보함과 동시에 연산시간까지 단축 가능한 유사 벡터 탐색 방식의 신호 예측 기법에 대한 적용 가능성을 평가한다. 원자력 발전소는 일정 주기로 계획예방정비를 반복 수행하기 때문에 기동운전구간에서의 신호 패턴을 주기적으로 확보할 수 있다. 따라서 과거 기동운전구간의 데이터 패턴을 각 알고리즘별로 학습하고 예측 결과를 비교하여 정확도 높은 최적의 상태감시 기법을 사용하도록 시스템을 제안하고 그 효과를 기술한다.

2. 기동운전구간 조기경보 시스템

원전 조기경보 시스템은 강한 상관관계 신호들을 군으로 선정하고 과거 정상운전 패턴을 학습하여 예측하는 AAKR(Auto-Associative Kernel Regression) 기법을 사용한다.⁵⁾ 기동운전구간은 정상운전구간 대비 짧은 기간이지만 계획예방정비 후 출력을 100%까지 도달하는 과정으로 신호군의 패턴 변화가 다양하고 신호 간의 상관관계 또한 약해진다. 따라서 기동운전구간과 같이 여러 운전 환경 요소에 의하여 약한 상관관계를 갖거나 신호 간의 연관성보다 기기 및 시스템의 연계성을 우선으로 구성되는 경우에 대한 고장감지 기법의 보완이 필요하다. 이를 해결하기 위해 근사 근접 이웃 탐색 방식인 ANNS(Approximate Nearest Neighbor Search) 기법을 사용하여 인덱스 모델을 구축하고 현재값과 가장 유사한 과거 예측값을 모델에서 탐색 후 실측값과의 잔차(Residual)를 비교함으로써 결함 유무를 판정한다.

본 논문에서는 다양한 근사 근접 이웃 탐색 기법 중 신호 이상치 탐지에 주로 사용되는 ANNOY 기법을 결합하여 성능을 평가하였다. ANNOY 기법은 Spotify.com에서 개발하여 추천 서비스 엔진으로 사용되고 있는 대표적인 근사 근접 이웃 탐색 기법이다. ANNOY는 Fig. 1과 같이 Random projection을 이용하는 기법으로 사용자가 설정한 Tree node 수에 맞추어 벡터 공간의 초평면(Hyperplane)을 찾아 반복적으로 구역을 나누어 인덱스 모델을 구축한다.⁶⁾ 이러한 인덱스 모델을 기반으로 새로 입력된 신호 정보가 속하는 Tree node를 찾고 해당 구간에서 가장 유사한 과거 벡터 정보를 예측값으로 산출한다.⁷⁾

Fig. 1

Model decision scheme for fault detection

원전 조기경보 시스템의 신호군은 대부분 10개 이하의 신호들로 이루어져 있어 ANNOY 기법을 적용하기 적합하며 메모리 맵 파일을 통해 가상 메모리 주소로 접근하는 방식으로, AAKR 대비 최소한의 메모리로 빠르게 연산이 가능하다.

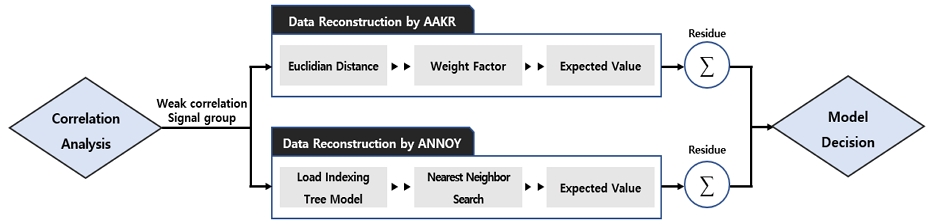
Fig. 2는 본 논문에서 제안하는 기동운전구간 조기경보 시스템이다. 기존 조기경보 시스템과 동일하게 신호 간의 상관분석(Correlation analysis)을 먼저 수행하고 약한 상관관계를 갖는 신호군의 경우 AAKR과 ANNOY 기법을 모두 적용하여 학습 모델을 구축 후 예측값을 산출하여 정확도가 더 높은 기법을 최종 감시모델로 사용한다.

3. 시스템 성능 실험

3.1 약한 상관관계 신호 모델 적용

3.1.1 실험 절차 및 내용

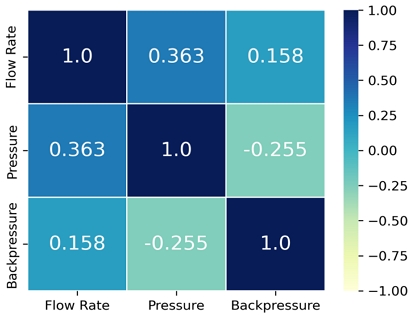
실험 대상은 실제 조기경보 시스템에서 운영하고 있는 신호군 중에서 약한 상관관계를 갖는 모델을 선정하였다. 선정 신호군은 유량 계측 신호, 압력 계측 신호, 배압 계측 신호로 구성되어 있으며, 피어슨 상관 계수(Pearson correlation coefficient)로 분석한 결과는 Fig. 3과 같다. 피어슨 상관 계수는 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 상관관계, -1은 완벽한 음의 상관관계를 의미한다. 유량 계측 신호와 압력 계측 신호는 0.363, 유량 계측 신호와 배압 계측 신호는 0.158, 압력 계측 신호와 배압 계측 신호는 -0.255로 모두 상관관계가 약한 신호군이다.

Fig. 3

Correlation Analysis Matrix

거리 계산 방식은 기존 조기경보 시스템과 동일한 신호군의 과거 계측 시계열 데이터는 총 40,320건 수집하여 Train set과 Test set으로 분리하여 사용하였다. AAKR 기법의 Kernel bandwidth와 ANNOY 기법의 Tree node 수 및 인접 벡터 탐색 수는 반복 실험을 통해 최적의 결과를 산출하는 값으로 설정하였다. 상세 실험 설정 정보는 Table 1과 같다.

Table 1

Dataset & parameter summary

Euclidean distance로 산출하였으며, 예측 정확도는 실측값 Y와 예측값 $$ \widehat{Y}$$의 차이를 제곱하여 평균화한 평균제곱오차 MSE(Mean Squared Error)를 사용하였다.

$\[ MSE=\frac{1}{n}\sum _{i=1}^n{\left({\widehat{Y}}_i-Y_i\right)}^2 \]$

(1)

3.1.2 실험 결과

알고리즘의 연산시간은 동일한 실험조건에서 수행하였으며, Table 2와 같이 Train set, Test set 모두 ANNOY 기법이 3배 이상 빠른 결과를 보였다. 신호별 MSE 차이 또한 Train set을 기준으로 ANNOY 기법이 AAKR 대비 유량 계측 신호는 34배 이상, 압력 계측 신호는 7배 이상, 배압 계측 신호는 15배 이상 정확함을 보였다. 해당 모델의 검증을 위하여 Test set을 입력 후 산출한 결과, ANNOY 기법이 AAKR 대비 유량 계측 신호는 13배 이상, 압력 계측 신호는 4배 이상, 배압 계측 신호도 4배 이상 정확함을 보였다.

Table 2

Reconstruction time & MSE

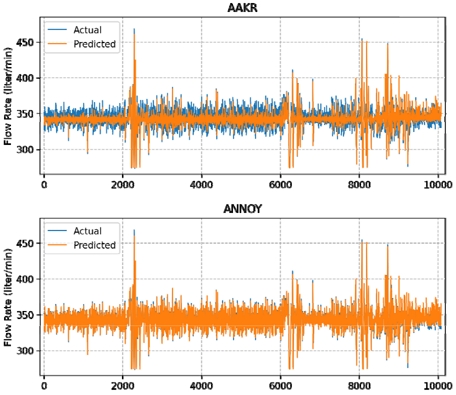
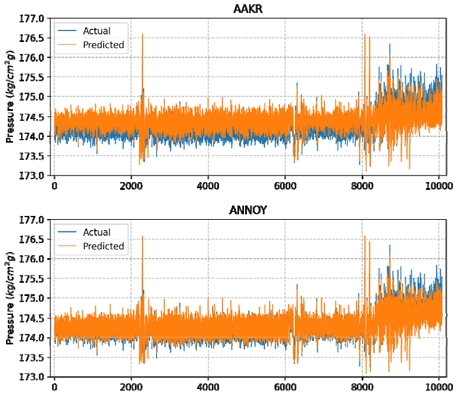
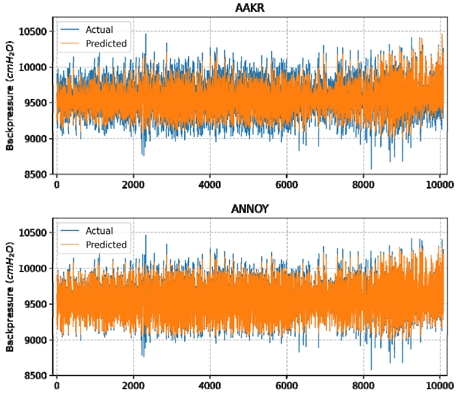
Fig. 4~6은 Test set의 각 신호별 실측값과 예측값을 함께 표현한 결과를 보여 준다.

Fig. 4

Time-series Graphs of Flow Rate Test set

Fig. 5

Time-series Graphs of Pressure Test set

Fig. 6

Time-series Graphs of Backpressure Test set

유량 계측 신호, 압력 계측 신호, 배압 계측 신호 모두 ANNOY 기법이 AAKR 대비 실측값과 예측값의 차이인 잔차가 작아 그래프로도 정교하게 예측이 가능함을 확인하였다.

3.2 기동운전구간 신호 모델 적용

3.2.1 실험 절차 및 내용

기동운전구간 신호 모델 실험의 대상 학습 데이터는 n-1회차 기동운전구간의 시계열 데이터 총 13,501건을 수집하여 신호군 별로 모델을 구축하였고, 실험 데이터는 n회차 기동운전구간의 시계열 데이터 총 4,490건을 사용하였다. ANNOY 기법에서 유사도가 높은 벡터값이 초평면의 경계선에 위치할 경우, 예측 정확도가 부정확할 수 있기 때문에 우선순위를 고려하여 인접한 10개의 벡터 정보를 탐색 후 평균값으로 보정하도록 하였다.

AAKR 기법의 Kernel bandwidth와 ANNOY 기법의 트리 노드 수는 반복 실험을 통해 최적의 결과를 산출하는 값으로 설정하였다. 상세 실험 정보는 Table 3과 같다.

Table 3

Summary of dataset & Parameters

예측 정확도 판별은 기존 조기경보 시스템과 동일하게 Euclidean distance로 산출하였으며, 평균제곱오차(MSE)를 예측 정확도 판별 지표로 사용하였다.

3.2.2 실험 결과

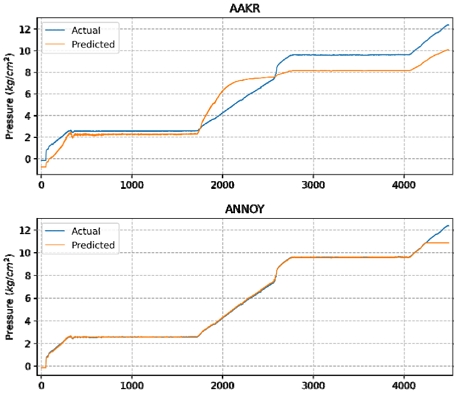
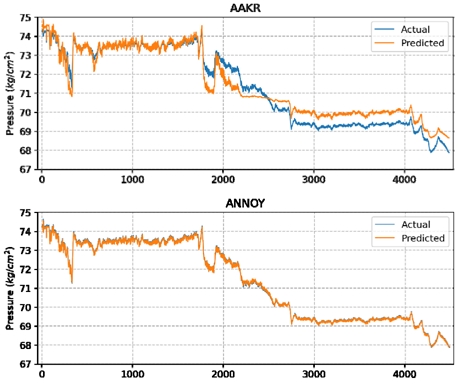
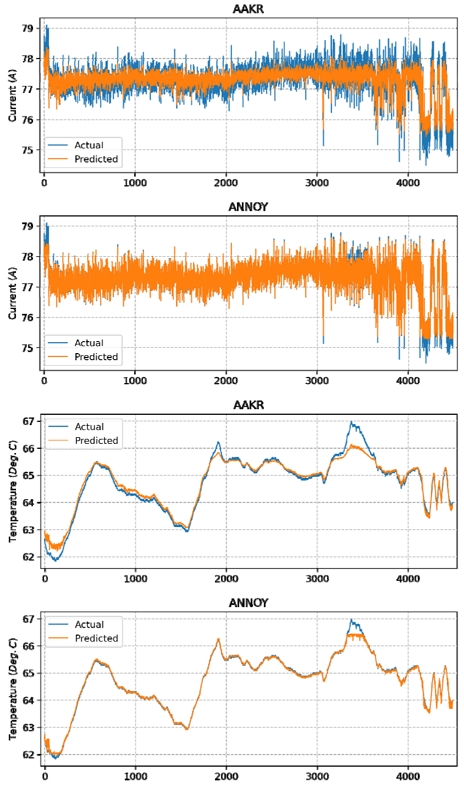
증가 추세 신호군은 총 3개의 압력 계측 신호로 구성되어 있으며 MSE 비교 결과, ANNOY 기법이 AAKR 대비 평균 29.6배 이상 정확함을 보였다. 감소 추세 신호군은 총 3개의 압력 계측 신호로 구성되어 있으며, ANNOY 기법이 평균 218배 이상 정확함을 보였다. 마지막으로 서로 다른 물리 단위를 갖는 모델은 전류 계측 신호 1개와 온도 계측 신호 3개로 구성되어 있으며, ANNOY 기법이 AAKR 대비 전류 계측 신호는 15배, 온도 계측 신호는 평균 5.9배 정확함을 보였다. 기동운전구간 실험 모델 그룹의 신호 구성과 알고리즘에 따른 신호별 MSE 실험 결과는 Table 4와 같다.

Table 4

MSE of residuals for each group

Fig. 7~9는 각 모델 그룹에서 대표 신호를 선별하여 실측값과 예측값을 함께 표현한 것으로, ANNOY 기법이 AAKR 대비 잔차가 작아 정교하게 예측 가능함을 확인하였다.

Fig. 7

Pressure 1 results of the increasing trend group

Fig. 8

Pressure 1 results of the decreasing trend group

Fig. 9

Current & Temperature 1 results of the different physical unit group

4. 결 론

원전 기동운전구간의 경우, 신호 변화 패턴이 다양하여 기존의 통계 기반 예측 기법으로는 예측 오차가 허용 수준 이상으로 발생할 수 있다. 따라서 과거 데이터 패턴을 학습하여 인덱스 트리를 만들고 근사 근접 이웃 탐색을 통해 예측 오차를 줄일 수 있는 방법을 함께 고려하여 최종 예측을 수행하는 시스템을 제안하였다. 시스템은 기존 통계 기반의 예측 기법 대비 연산 속도가 빠르면서 신호 예측 정확도까지 개선이 가능함을 실험을 통해 확인하였다. 이는 실제 운전 과정에서 이상징후 발생 시보다 빠른 시점에 잔차 변화를 감지할 수 있어 약한 상관관계 신호군에서도 조기경보 신뢰성 향상이 가능하다. 또한 기동운전구간을 대표하는 증가 추세, 감소 추세, 서로 다른 물리 단위를 갖는 신호군을 선정하여 비교한 결과, 모두 예측 정확도가 우수함을 실험을 통해 확인하였다. 시스템을 적용할 경우 기동운전 과정에서 이상징후 발생 시보다 빠른 시점에 잔차 변화를 감지함으로써 조기에 경보 알림 및 조치가 가능하여 안전하게 정상출력까지 도달하도록 보완할 수 있다.

Author contributions

J. H. Kang; Investigation, Conceptualization, Data curation, Validation, Visualization, Writing-original draft. J. H. Min; Methodology, Supervision, Writing-review & editing.

References

• J. H. Min, D. W. Kim and C. Y. Park, 2019, “Demonstration of the validity of the early warning in online monitoring system for nuclear power plants”, Nuclear Engineering and Design, 349, 56-62. [https://doi.org/10.1016/j.nucengdes.2019.04.028]
• J. H. Min, S. G. Lee and D. W. Kim, 2018, “Development of Early Warning Model Based on Patter Learning for the Operation Condition in Nuclear Power Plant”, Journal of the Korea Society for Power System Engineering, 22(4), 17-23. [https://doi.org/10.9726/kspse.2018.22.4.017]
• J. Y. Jung, B. O. Lee, H. K. Kim and D. W. Kim, 2016, “Performance Analysis on Ealry Detection of Fault Symptom of a Pump with Abnormal Signals”, Journal of Power System Engineering, 20(2), 66-72. [https://doi.org/10.9726/kspse.2016.20.2.066]
• P. Baraldi, R. Canesi, E. Zio, R. Seraoui and R. Chevalier, 2011, “Signal grouping for condition monitoring of nuclear power plant components”, Reliability and Risk Management ESREL, 1-13.
• F. D. Mario, P. Baraldi, E. Zio and R. Seraoui, 2013, “Fault detection in nuclear power plants components by a combination of statistical methods”, IEEE Transactions on Reliability, 62(4), 833-845. [https://doi.org/10.1109/TR.2013.2285033]
• S. Dasgupta and Y. Freund, 2008, “Random projection trees and low dimensional manifolds”, Proceedings of the fortieth annual ACM symposium on Theory of computing. [https://doi.org/10.1145/1374376.1374452]
• W. Li, Y. Zhang, Y. Sun, W. Wang, M. Li, W. Zhang and X. Lin, 2019, “Approximate nearest neighbor search on high dimensional data - experiments, analyses, and improvement”, IEEE Transactions on Knowledge and Data Engineering, 32(8), 1475-1488. [https://doi.org/10.1109/TKDE.2019.2909204]