자이로 안정화 감시시스템의 미지입력 관측기 기반 제어시스템 설계에 관한 연구

1. 서 론

본 논문에서는 차량에 카메라를 장착하여 이동하며 주변을 감시하는 시스템의 모션 제어시스템 설계법에 대해 다룬다. 특히, 짐벌 메커니즘을 적용하여 카메라 LOS(Line of Sight) 안정화 제어문제를 고려한다. 짐벌 안정화 제어문제가 광범위하게 연구되었음에도 동적시스템의 복잡성, 갑작스러운 차량 기동, 예기치 못한 목표물 이동 및 기타 다양한 외란으로 인해 다루기 까다로운 것이 현실이다.^1-4) 최근 자동화 추세는 네트워크 기반 제어시스템 구축 비용 감소로 인해 경제적 관점에서 큰 이점을 달성하고 있어 이를 다양하게 적용하고 있다. 그러나 네트워크 기반 저비용 제어시스템 장치는 일반적으로 시간지연 혹은 신뢰할 수 없는 동작과 같은 문제점이 따르게 된다.

이를 해결하기 위한 연구사례 중 대표적인 고전적 제어전략으로 두 개 루프를 갖는 제어시스템이 있다. 첫 번째, 속도제어 루프는 LOS를 안정화하고, 상기 언급한 외란을 LOS로부터 억제시키는 제어목적을 갖는다. 두 번째는 추종제어 루프이며 LOS가 목표물을 지향할 수 있도록 한다. 따라서 일반적으로 cascade 제어기법이 사용된다.^2-5) 최근 연구사례에서는 목표물 추종 및 외란 억제 제어목적을 동시에 달성할 수 있는 강인제어기법이 적용되었다. 예를 들어 슬라이딩모드제어(SMC), H_∞, 능동 외란 제거 제어(ADRC) 등이 우수한 강인성과 효율적 제어목적 달성으로 인해 널리 사용되고 있다.^6-9) 이를 통해 짐벌 시스템 제어성능을 향상하기 위한 가장 효과적인 방법은 능동적인 외란 제거가 가능한 외란 관측기와 강인제어기 결합하는 것임을 알 수 있다. 여기서 관측기는 외부로부터 유입되는 외란과 모델링되지 않은 동역학의 영향을 추정하며, 결국 제어입력을 통해 강인성 향상 및 추정오차를 산출한다. Li and Yu는 이중 짐벌 제어 모멘트 자이로를 위해 적분형 SMC(ISMC) 및 차수감소 cascade 확장 상태 관측기를 결합하였다.¹⁰⁾ Kurkcu et al.은 외란 및 불확실성 추정기 기반 ISMC를 도입하였다.¹¹⁾ 여기서 외란 및 불확실성 추정기는 등가 입력외란에 기반하여 설계되었으며, 강인제어기 설계법에 따라 전개되었다. 최신 연구에서는 관측기와 제어기 설계를 위해 SMC의 강인성 특징을 활용하였다. 고차 슬라이딩모드 관측기는 연속 터미널 SMC와 슈퍼 트위스팅 SMC를 결합하여 설계되었다.^6,12) 그러나 시간지연과 같은 제약이 시스템에 존재하는 경우 앞서 언급한 접근법은 우수한 제어성능을 확보하는데 어려움이 있다.

입력지연의 경우 다양한 고전적 접근법이 제시되고 있다.^13-15) 복잡한 시스템의 경우 다루기 어려우나 그렇지 않으면 현재 제어 신호와 지연 제어신호 차이를 입력 외란으로 고려하여 정합외란 억제 제어목적을 달성할 수 있다. Zhu et al.에서는 해당 값을 추정하기 위한 능동기법을 적용하고, 반균일궁극유계(semi-uniform ultimate boundedness) 조건을 만족시키는 백스테핑(backstepping) 제어기를 설계하였다.¹⁶⁾ 또한 정합외란은 SMC 및 강인제어기법으로 해결할 수 있다. 그러나 대부분, 지연에 따른 영향을 완벽히 제거하기 어려운 것이 현실이다. SMC의 불연속적 특성으로 인해 잔여진동이 존재하거나 지연시스템의 안정성이 보장되는 한편 실시간 응답을 받을 수 없다.

그러므로 본 논문에서는 외부로부터 유입되는 외란과 시간지연을 보상함으로써 우수한 추종성능을 갖는 새로운 형태의 짐벌 안정화 제어시스템을 제안한다. 이를 위해 대상 시스템의 수학적 모델을 도출하고, 제어시스템 설계 및 유효성 검증을 수행한다. 첫 번째는 외란과 지연에 따른 영향을 추정하기 위한 미지 입력 관측기(unknown input observer)를 도입한다. 두 번째로 ISMC와 슈퍼 트위스팅 알고리즘, 백스테핑 제어기법의 장점을 결합하여 강인한 제어입력을 설계한다. 세 번째로 시뮬레이션을 통해 제안하는 제어시스템 설계법의 유효성을 검증한다.

2. 시스템 모델링

본 논문에서 고려하는 자이로 안정화 카메라시스템을 Fig. 1에 나타내었다. 두 개의 벨트구동 서보로 구동되는 2축 짐벌 구조를 갖는다. 여기서, 제어입력은 팬, 틸트 짐벌 서보를 구동하는 속도 기준신호이다. 카메라는 틸팅 채널 중심부에 위치하며, 방위각은 AHRS(Attitude Heading Reference System)으로부터 계측된다.

Fig. 1

The gyro-stabilized surveillance system to be controlled

시스템의 기구학 및 동역학적 관계에 따라 대상시스템의 운동방정식은 다음과 같다.

여기서,

φ(t) : 틸팅 방위에 대한 틸트 및 팬 오일러각

ω(t) : 각속도 벡터

u(t-τ) : 시변 시간지연 τ에 대해 시간 (t-τ)에서 계산된 틸트 및 팬 짐벌의 속도 명령신호

d(t): 차량의 운동, 질량 불균형, 비선형 마찰 등에 대한 덩어리 외란

f_E(φ(t)): 시스템 행렬

그리고 시스템 행렬은 다음과 같다.

여기서, φ_tx(t)는 틸트 짐벌의 롤 오일러 각, θ(t)는 팬 짐벌에 대한 틸트 짐벌의 상대 운동을 나타낸다.

3. 운동제어시스템 설계

본 논문에서 제안하는 제어시스템의 목적은 주어진 목표물을 안정적으로 추종할 수 있는 제어기를 설계하는 것이다. 이 제어목적을 달성하기 위해 제어입력은 반드시 차량 운동으로 인한 외란과 시간지연 τ의 영향을 효과적으로 억제해야 한다. H_∞제어기법에 따르면, 지연 요소는 Fig. 2와 같이 곱셈형 불확실성으로 고려할 수 있다. 이는 지연신호의 라플라스 변환을 통해 쉽게 확인할 수 있다.

Fig. 2

The delayed input is represented by the current input and a multiplicative uncertainty

이에 따라 시스템 모델은 다음과 같이 나타낼 수 있다.

여기서,

e_u(t)는 등가 불확실성을 나타내므로 d(t)-B(t)e_u(t)는 결국 외란 및 지연으로 인한 전체 영향을 나타낸다. 또한 식 (3)과 식 (4)로부터 짐벌락(φ_tx(t)==π/2)을 벗어나면 Lipchitz 함수를 만족하는 것을 확인할 수 있다. 즉, 어떠한 X₁(t)와 X₂(t)에 대해서 다음을 만족하는 상수 κ가 존재한다.

3.2 강인제어기 설계

외란 추정과 제어시스템 강인성 확보를 동시에 달성하기 위하여 ISMC를 도입한다. 여기서, 제어입력은 공칭 모델에 대한 제어목적 달성을 위한 백스테핑 기반 등가 제어입력 u₀(t)와 슈퍼 트위스팅 알고리즘에 따른 강인제어입력 u_d(t)으로 구성된다.

$\[ u\left(t\right)=u_0\left(t\right)+u_d\left(t\right)-B^{-1}\left(t\right){\widehat{d}}_X\left(t\right) \]$

(13)

공칭 모델은 비이상적(non-ideal) 요소를 고려하지 않은 시스템으로 고려한다. 즉, 전체모델에서 외란과 지연요소를 제외한 모델을 의미한다. 제어기 설계를 위하여 추종오차 e_φ(t)와 안정화오차 e_ω(t)를 다음과 같이 정의한다.

$\[ \begin{array}{l}{e}_{\phi }\left(t\right)={\phi }_d\left(t\right)-\phi \left(t\right)\\ e_w\left(t\right)=\Lambda e_{\phi }\left(t\right)+{\dot{\phi }}_d\left(t\right)-f_E\left(\phi \left(t\right)\right)\omega \left(t\right)\end{array} \]$

(14)

여기서, Λ는 양정정 대각행렬이다. 리아푸노프 함수 V(t)를 식 (15)로 고려할 때, 등가제어 입력을 식 (16)으로 정의하면, 조건을 만족하게 된다. 이것은 두 가지 제어목적인 LOS안정화와 목표물을 이상적으로 추종할 수 있는 제어성능을 달성할 수 있음을 나타낸다.

$\[ V\left(t\right)=\frac{1}{2}{e}_{\phi }^T\left(t\right)e_{\phi }\left(t\right)+\frac{1}{2}{e}_{\omega }^T\left(t\right)e_{\omega }\left(t\right) \]$

(15)

$\[ u_0\left(t\right)=\begin{array}{l}{B}^{-1}\left(t\right)K\omega \left(t\right)+B{\left(t\right)}^{-1}{f}_E^{-1}\left(\phi \left(t\right)\right)\\ \left[\ddot{\phi }\left(t\right)+\left(I-{\Lambda }^2\right)e_{\phi }\left(t\right)-{\dot{f}}_E\left(\phi \left(t\right)\right)\right.\\ \left.\omega \left(t\right)+\left(\Gamma +\Lambda \right)e_{\omega }\left(t\right)\right]\end{array} \]$

(16)

$\[ \dot{V}\left(t\right)=-e_{\phi }^T\left(t\right)\Lambda e_{\phi }\left(t\right)-e_{\omega }^T\left(t\right)\Gamma e_{\omega }\left(t\right) \]$

(17)

강인제어입력 설계를 위해 먼저, 적분형 슬라이딩 매니폴드를 다음 식으로 정의한다.

$\[ s\left(t\right)=\begin{array}{l}{\dot{e}}_{\phi }\left(t\right)+\left(\Gamma +\Lambda \right)e_{\phi }\left(t\right)\\ +\left(I+\Gamma \Lambda \right){\int }_0^t e_{\phi }\left(t\right)dt\end{array} \]$

(18)

이에 대한 시간 미분은 다음과 같으며,

$\[ \dot{s}\left(t\right)=-f_E\left(\phi \left(t\right)\right)\left(B\left(t\right)u_d\left(t\right)-{\widehat{d}}_X\left(t\right)+d_X\left(t\right)\right) \]$

(19)

슈퍼 트쉬스팅 알고리즘에 따라 강인제어입력 u_d(t)는 다음과 같이 구할 수 있다.

$\[ \begin{array}{l}{u}_d\left(t\right)=\\ B^{-1}\left(t\right)f_E^{-1}\left(\phi \left(t\right)\right)G_1\left[\begin{array}{cc}{s}_1^{1/2}& sgn\left(s_1\left(t\right)\right)\\ s_2^{1/2}& sgn\left(s_2\left(t\right)\right)\end{array}\right]\\ +B^{-1}\left(t\right)f_E^{-1}\left(\phi \left(t\right)\right)G_2{\int }_0^t\left[\begin{array}{c}sgn\left(s_1\left(t\right)\right)\\ sgn\left(s_2\left(t\right)\right)\end{array}\right]dt\end{array} \]$

(20)

$$ {\left[s_1\left(t\right)s_2\left(t\right)\right]}^T=s\left(t\right),sgn\left(s_i\right)=s_i/\left(\left|s_i\right|+\delta \right)$$이며, δ는 양의 상수이다. G₁와 G₂는 양정정 대각행렬이다. 강인제어입력 식 (20)을 식 (19)에 대입하면 다음과 같이 정리된다.

$\[ \dot{s}\left(t\right)\le \begin{array}{l}-G_1\left[\begin{array}{cc}{s}_1^{1/2}& sgn\left(s_1\left(t\right)\right)\\ s_2^{1/2}& sgn\left(s_2\left(t\right)\right)\end{array}\right]\\ -G_2{\int }_0^t\left[\begin{array}{c}sgn\left(s_1\left(t\right)\right)\\ sgn\left(s_2\left(t\right)\right)\end{array}\right]dt\\ +\kappa f_E\left(\phi \left(t\right)\right)W‖\tilde{X}\left(t\right)‖\end{array} \]$

(21)

여기서, 제어기 이득과 대상시스템의 유계에 대한 필요조건은 Seeber et al., Moreno et al.에 따라 쉽게 구할 수 있다.^17,18) 설계한 제어입력 즉, 본 논문에서 제안하는 제어시스템을 Fig. 3에 블록선도로 나타내었다.

Fig. 3

Block diagram of the proposed control system

4. 결과 및 고찰

4.2 시뮬레이션 결과

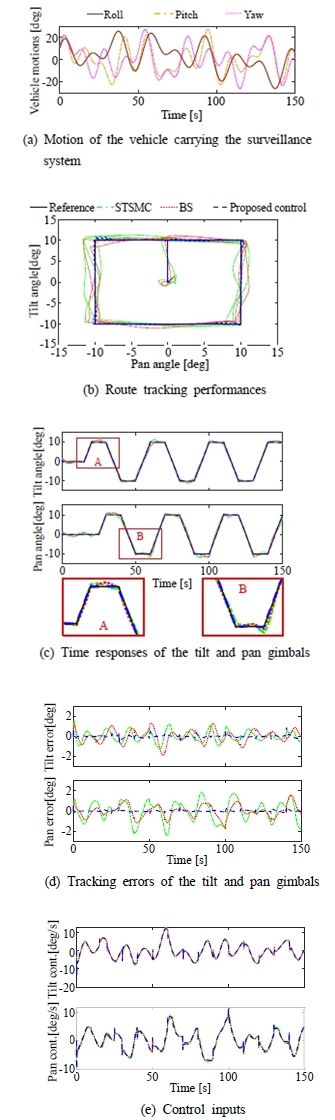
Fig. 4 (a)에 나타낸 바와 같이 목표물이 차량에 운반되는 동안 이동하는 궤적을 추종하는 시뮬레이션을 수행하였으며, Fig. 4(b)~(e)에 시뮬레이션 결과를 나타내었다. Fig. 4(b), (c)에서 확인 가능하듯이 본 논문에서 제안하는 제어시스템의 추종성능이 가장 우수하게 나타났다. 본 논문에서 제안하는 제어시스템은 외란과 지연에 따른 영향을 추정하여 이를 제어입력에 인가하고, ISMC로 인해 대상시스템의 강인성을 향상시킬 뿐 아니라 잔여 추정오차를 보상하였으므로 우수한 추종성능을 확보하고 외란을 효과적으로 억제하였다. 한편, STSMC와 TDC-BS 제어기를 적용한 경우, Fig. 4(d)에서 확인 가능하듯이 차량 운동 진폭을 고려할 때 외란을 억제하였음을 알 수 있으나, 지연과 외란에 대한 추정값이 부정확하여 충분히 억제하지 못하였다. 마지막으로 Fig. 4(e)는 제어기로부 터 생성된 서보 액추에이터에 대한 속도명령 신호를 나타낸다.

Fig. 4

Simulation results

4.3 실험 결과

제어시스템 실험 및 성능평가를 위해 본 논문에서 제안하는 제어기를 실험모델에 적용하였고, 용한 실험장치를 Table 2에 간략히 나타내었다.

Table 2

Experimental apparatus specifications

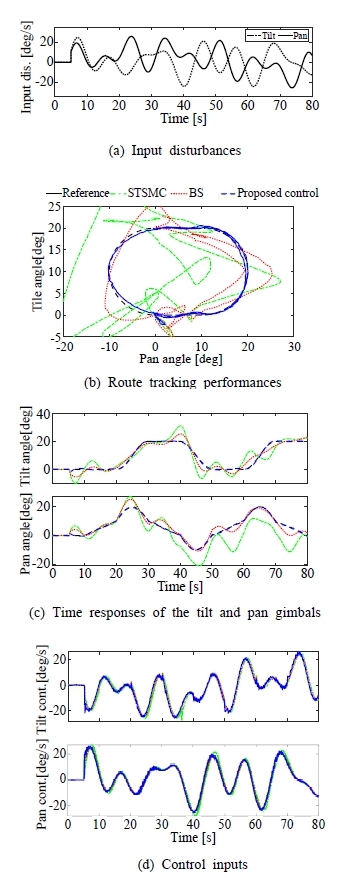
실험에서는 Fig. 5 (a)에 나타낸 것과 같은 입력 외란을 고려하였으며, 시스템 응답을 Fig. 5 (b)~(d)에 나타내었다. 시뮬레이션에서 나타난 경향과 비슷하게 본 논문에서 제안하는 제어시스템의 외란 억제 성능이 가장 우수한 것으로 나타났다. 특히, 본 논문에서 제안하는 제어기를 적용한 경우 틸트 운동의 RMS가 TDC-BS대비 84.38% 감소하였으며, STSMC의 경우 다른 두 제어기를 적용한 결과, 대비 현저히 나쁜 제어성능을 나타내었다. 팬 운동의 경우에도 마찬가지로 본 논문에서 제안하는 제어기를 적용한 결과, 외란의 영향을 효과적으로 억제하였음을 확인할 수 있다. 입력 지연으로 인한 잔여진동이 추종경로에 발생하였으나 제어목적 달성에 문제되지 않는 수준임을 확인하였다.

Fig. 5

Experimental results

결국 본 논문에서 제안하는 제어기를 적용한 결과 외란과 지연의 영향을 관측기를 통해 추정하였기 때문에 우수한 추종성능을 확보하였다. 그러나 시뮬레이션에 반영되지 않은 실험장치의 외란과 지연의 영향으로 인해 비교 대상 두 제어기의 제어성능이 시뮬레이션 대비 실험결과에서 현저히 저하된 결과를 나타내었다.

4. 결 론

본 논문에서는 시간지연과 외란에 영향을 받는 짐벌 자이로 안정화 시스템에 대한 강인제어 전략을 제안하였다. 외란과 지연의 영향을 미지 입력 관측기를 통해 추정하기 위해 시스템 입력과 시스템 동특성으로부터 외란과 지연의 영향을 비연성화되도록 게인을 설계하였다. 그리고 백스테핑, 적분형 슬라이딩모드 및 슈퍼 트위스팅 알고리즘을 결합한 제어기를 설계하였다. 시뮬레이션과 실험을 통해 제안하는 제어시스템의 유효성을 검증하였으며, 특히 시간지연 보상 백스테핑 제어기, 슈퍼 트위스팅 알고리즘 기반 제어기를 각각 적용한 경우와 비교 평가를 수행하였다. 결론적으로 본 논문에서 제안하는 제어시스템은 다른 제어시스템과 비교하여 외부 외란이 존재하는 경우에도 우수한 제어성능을 확보할 수 있음을 나타내었다.

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(2022년)에 의하여 연구되었음.

References

• J. M. Hilkert, 2008, “Inertially stabilized platform technology Concepts and principles”, IEEE Control Systems, 28(1), 26-46. [https://doi.org/10.1109/MCS.2007.910256]
• M. K. Masten, 2008, “Inertially stabilized platforms for optical imaging systems”, IEEE Control Systems, 28(1), 47-64. [https://doi.org/10.1109/MCS.2007.910201]
• P. J. Kennedy and R. L. Kennedy, 2003, “Direct versus indirect line of sight (LOS) stabilization”, IEEE Transactions on Control Systems Technology, 11(1), 3-15. [https://doi.org/10.1109/TCST.2002.806443]
• S. Liu, T. Lu, T. Shang and Q. Xia, 2018, “Dynamic Modeling and Coupling Characteristic Analysis of Two-Axis Rate Gyro Seeker”, International Journal of Aerospace Engineering, 2018, 1-14. [https://doi.org/10.1155/2018/8513684]
• M. F. Reis, J. C. Monteiro, R. R. Costa and A. C. Leite, 2019, “Super-Twisting Control with Quaternion Feedback for a 3-DoF Inertial Stabilization Platform”, Proceedings of the IEEE Conference on Decision and Control 2018-December, 2193-2198. [https://doi.org/10.1109/CDC.2018.8619292]
• J. Mao, J. Yang, X. Liu, S. Li and Q. Li, 2020, “Modeling and Robust Continuous TSM Control for an Inertially Stabilized Platform With Couplings”, IEEE Transactions on Control Systems Technology, 28(6), 2548-2555. [https://doi.org/10.1109/TCST.2019.2933382]
• G. Suoliang, Z. Lei, P. Zhaowu and Y. Shuang, 2018, “Finite-time Robust Control for Inertially Stabilized Platform Based on Terminal Sliding Mode”, in IEEE 37th Chinese Control Conference, 483-488. [https://doi.org/10.23919/ChiCC.2018.8483114]
• D. H. Lee, D. Q. Tran, Y. B. Kim and S. Chakir, 2020, “A robust double active control system design for disturbance suppression of a two-axis gimbal system”, Electronics, 9(10), 1-18. [https://doi.org/10.3390/electronics9101638]
• J. Han, 2009, “From PID to Active Disturbance Rejection Control”, IEEE Transactions on Industrial Electronics, 56(3), 900-906. [https://doi.org/10.1109/TIE.2008.2011621]
• H. Li and J. Yu, 2020, “Anti-Disturbance Control Based on Cascade ESO and Sliding Mode Control for Gimbal System of Double Gimbal CMG”, IEEE Access, 8, 5644-5654. [https://doi.org/10.1109/ACCESS.2019.2963079]
• B. Kurkcu, C. Kasnakoglu and M. O. Efe, 2018, “Disturbance/Uncertainty Estimator Based Integral Sliding-Mode Control”, IEEE Transactions on Automatic Control, 63(11), 3940-3947. [https://doi.org/10.1109/TAC.2018.2808440]
• A. Chalanga, S. Kamal, L. M. Fridman, B. Bandyopadhyay and J. A. Moreno, 2016, “Implementation of Super-Twisting Control: Super-Twisting and Higher Order Sliding-Mode Observer-Based Approaches”, IEEE Transactions on Industrial Electronics, 63(6), 3677-3685. [https://doi.org/10.1109/TIE.2016.2523913]
• Q. C. Zhong, 2006, “Robust control of time-delay systems”, Robust Control of Time-delay Systems. [https://doi.org/10.1007/1-84628-265-9]
• J. Y. Choi and M. Krstic, 2016, “Compensation of time-varying input delay for discrete-time nonlinear systems”, International Journal of Robust and Nonlinear Control, 26(8), 1755-1776. [https://doi.org/10.1002/rnc.3382]
• T. Huynh, H. C. Park, D. H. Lee and Y. B. Kim, 2021, “A Study on a Vision-Based Target Tracking Control System Design”, Journal of Power System Engineering, 25(1), 13-22. [https://doi.org/10.9726/kspse.2021.25.1.013]
• Q. Zhu, T. Zhang and S. Fei, 2010, “Adaptive tracking control for input delayed MIMO nonlinear systems”, Neurocomputing, 74(1-3), 472-480. [https://doi.org/10.1016/j.neucom.2010.03.003]
• R. Seeber and M. Horn, 2017, “Stability proof for a well-established super-twisting parameter setting”, Automatica, 84, 241-243. [https://doi.org/10.1016/j.automatica.2017.07.002]
• J. A. Moreno and M. Osorio, 2012, “Strict Lyapunov Functions for the Super-Twisting Algorithm”, IEEE Transactions on Automatic Control, 57(4), 1035-1040. [https://doi.org/10.1109/TAC.2012.2186179]
• H. C. Park, S. Chakir, Y. B. Kim and T. Huynh, 2021, “A Nonlinear Backstepping Controller Design for High-Precision Tracking Applications with Input-Delay Gimbal Systems”, Journal of Marine Science and Engineering, 9(5), 530. [https://doi.org/10.3390/jmse9050530]
• T. Huynh and Y. B. Kim, 2021, “A Study on Gimbal Motion Control System Design based on Super-Twisting Control Method”, Journal of the Korean Society for Precision Engineering, 38(2), 115-122. [https://doi.org/10.7736/JKSPE.020.077]
• T. Huynh, M. T. Tran and Y. B. Kim, 2021, “An Anti-disturbance Backstepping Control for A Two-axis Gimbal System with Euler Angle Feedback and Delayed Inputs”, in 2021 IEEE International Conference on System Science and Engineering, 50-55. [https://doi.org/10.1109/ICSSE52999.2021.9538415]