냉각탑용 복합재 커플링 설계 및 제조

1. 서 론

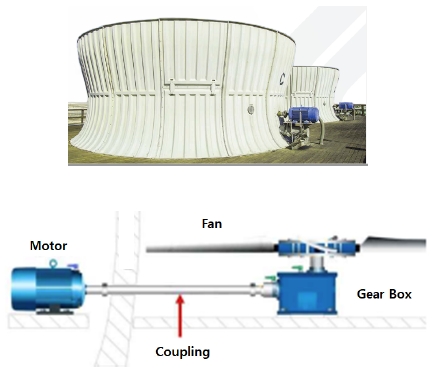
높은 내부식성과 경량이면서 강도와 강성이 매우 높은 특성으로 인하여 고분자 복합재료는 구조용 재료로서 적용이 점차 확대되고 있다.¹⁾ 특히, 원통형 복합재는 인장, 압축, 굽힘, 비틀림 등의 다양한 단순 하중뿐만 아니라 복합 하중에 대하여 견딜 수 있기 때문에 항공우주, 해양선박, 자동차, 화학 플랜트, 토목건축, 풍력 발전기 분야 등 그 사용 범위가 매우 넓다.^2-6) 이러한 복합재료의 장점을 활용하여 적용이 확대되고 있는 분야는 냉각탑에 사용되는 구조물이다. 냉각탑의 팬은 외부에 설치된 구동모터에서 장축 커플링을 통해 동력을 전달받아 회전하는 구조이다. Fig. 1은 냉각탑의 냉동 공조 시스템 사진과 개념도이다. Fig. 2는 장축커플링 구성 개념도를 보인 것이다. 장축커플링은 금속재의 경우에는 중량을 분산하기 위해 그 중간에 베어링을 설치해야 하는 경우도 있으며, 포화습공기에 의한 부식을 방지하기 위해 스테인리스 재질의 스페이서를 적용하고 있다. 또한 금속 스페이서는 고속 회전 시 휨 현상이 발생하여 진동 소음을 발생하고 있다. 따라서 탄소섬유 복합소재로 대체함으로써 경량화 및 냉각탑 설치와 유지 보수가 용이하고 진동 감소를 통한 소음의 최소화 및 피로 수명 연장이 가능하다.

Fig. 1

Cooling tower

Fig. 2

Schematic of a coupling

원통형 복합재료 튜브는 주로 필라멘트 와인딩성형법으로 제조하며 보강재 종류와 섬유배열 각도에 따라 복합재의 기계적 특성이 크게 달라진다. Herna´ndez-Moreno⁷⁾은 필라멘트 와인딩된 유리섬유/에폭시 실린더가 외부 압력을 받을 때의 기계적 거동에 대한 와인딩 패턴의 영향을 연구하였다. Herna Talib⁸⁾의 튜브형 샤프트에 대한 수치 해석 결과에서는, 적층 각도에 따라 강도의 최댓값은 최솟값보다 46% 증가될 수 있음을 보여 주었다. Badie⁹⁾는 유리섬유에 비하여 카본섬유가 복합재의 비틀림 강성이 증가하며 적층 각도 45°의 경우 비틀림 강성이 최대가 됨을 보였다.

Gireesh¹⁰⁾는 45° 적층 각도의 드라이브 샤프트는 같은 크기의 비틀림 강도를 가지는 강재 대비 72%의 무게 절감을 보고하였다. Colombo¹¹⁾의 수치해석 연구에서는, 최적의 섬유체적율과 와인딩 각도는 각각 40~60%와 44.5~52.5°임을 보고하였다.

기존의 연구는 원하는 기계적 특성을 얻기 위한 섬유배열 각도를 최적화하거나 다양한 시험에 관한 연구가 주로 이루어져 왔다. 그러나 복합재료 제조 중에 발생하는 문제로 인한 치수 정밀도에 관련한 연구는 거의 이루어진 바가 없다. 특히, 복합재료가 회전체로 사용될 때 형상과 치수 정밀도가 미달하는 경우 여러 문제가 발생될 수 있다. 따라서 본 논문에서는 필라멘트 와인딩에서 사용하는 맨드렐의 형상과 치수에 따른 복합재의 굴곡을 확인하고 이를 최소화할 수 있는 방안을 제시하였다. 또한 복합재 튜브의 기계적 성능과 와인딩 용이성 및 생산속도를 고려한 최적의 각도를 결정하고자 한다. 이를 위해 복합재 파이프의 구조 해석에 필요한 복합재의 기본 물성치를 확보하였고, 다양한 적층각도에 대한 구조 강도해석을 하였으며, 결정된 적층각도의 패턴으로 필라멘트 와인딩 장비를 이용하여 복합재료 파이프를 제작하였다.

2. 필라멘트 와인딩 성형법

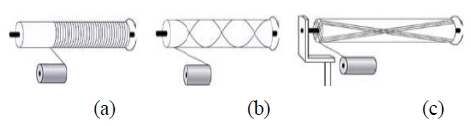
복합재료 성형법 중에서 축대칭 형상을 제조하는 대표적인 방법인 필라맨트 와인딩 성형법은 섬유를 감는 방식에 따라 Fig. 3에 보는 바와 같이 후프(Hoop) 와인딩, 헬리컬(Helical) 와인딩 그리고 측지선(Polar) 와인딩으로 구분할 수 있다. 필라멘트 와인딩 성형법에 의한 복합재 제조는 다음과 같은 순서로 진행된다(Fig. 4).

• (i) 수지함침된 섬유 투입
• (ii) 정해진 패턴으로 와인딩
• (iii) 경화
• (iv) 탈형

Fig. 3

Basic pattern of filament winding: (a) hoop winding; (b) helical winding; (c) polar winding

Fig. 4

Schematic of filament winding process

복합재료의 기계적 특성을 좌우하는 것은 섬유 배열방향과 섬유체적률인데, 복합재 구조물에 작용하는 하중 방향으로 섬유를 주로 배열하고 섬유체적율을 증가시키는 것이 중요하다.

3. 맨드렐 설계

필라멘트 와인딩에 사용하는 맨드렐은 표면을 연마한 강재(steel)을 사용한다. Fig. 5는 멘드렐을 보여 주고 있다. 와인딩이 완료되면 맨드렐은 수지가 함침된 보강섬유와 함께 회전하면서 경화 공정을 거치게 되는데, 이때 90℃ 이상의 고온에 놓여지므로 맨드렐 무게와 온도의 영향으로 처짐이 일어난다. 이로 인하여 복합재도 변형이 일어나기 때문에 맨드렐의 설계는 복합재의 변형을 최소화 하기 위해 중요하다. 맨드렐의 처짐량에 영향을 주는 것은 재료의 탄성계수, 단면 2차모멘트, 작용하는 하중 및 길이이다. 경화 오븐 내에서 회전시킬 때 한쪽 끝은 척과 같은 장치로 고정하고 맨드렐의 다른 쪽 끝은 길이 방향으로 자유롭게 움직이도록 한다. 이와 같은 경계 조건에서 맨드렐의 최대 처짐량 (δ)은 다음 식으로 표시된다.

Fig. 5

A mandrel for filament winding

여기서, ω는 분포하중으로서 단위길이 당 무게이며, l은 맨드렐의 길이, E 는 재료의 탄성계수, I는 맨드렐의 2차 단면계수이다. ω와 I는 단면의 형상과 관련이 있으며 맨드렐의 단면은 보통 원형이거나 무게를 줄이기 위해 튜브형을 사용한다. 식 (1)로부터 원형 맨드렐의 처짐량과 튜브형 맨드렐의 처짐량 비를 구하면 다음과 같다.

여기서, 첨자 s 및 t는 각각 원형(solid) 단면과 튜브형(tube) 단면을 의미한다. 2차 단면계수 I_s 와 I_t 는 다음과 같다.

여기서, D와 d는 각각 원형 혹은 튜브 단면의 외경 및 내경이다. 즉, 외경이 같을 때의 원형과 튜브형 단면의 처짐량을 비교하기 위한 것이다.

식 (2)에서 맨드렐의 무게는 단면적에 비례함을 고려하고 식 (3)을 대입하여 정리하면 단면이 원형일 때와 튜브형일 때의 최대처짐량 비율은 다음 식 (4)로 구해진다.

이 식에서, 튜브형 단면을 가지는 맨드렐이 원형 맨드렐에 비하여 최대 처짐량이 항상 작게 나타남을 알 수 있다.

본 연구에서는 실제로 사용되고 있는 냉각탑용 복합재 파이프의 크기를 참고하여 맨드렐을 설계하였으며, 그 크기를 Table 1에 정리하였다. 이렇게 설계된 맨드렐 크기에 대한 최대 처짐량 차이를 살펴보고자 한다. 먼저, 맨드렐 단면 형상이 원형인 경우와 튜브형인 경우에 대해 맨드렐 직경 변화에 따른 처짐량을 비교하였다. Table 2는 세 종류의 직경일 때의 단면 형상 차이에 따른 처짐량 비율을 보인 것이다. 이 표에서 보는 바와 같이, 튜브형이 원형 맨드렐보다 1.6배 이상 작은 처짐량을 보인다. 따라서 와인딩 복합재의 치수 정밀도를 유지하기 위해서는 튜브형 맨드렐을 사용하는 것이 필요함을 알 수 있다.

Table 1

Dimension of tube section mandrel

Table 2

Deflection ratio of mandrels with different diameters

Table 1에 나와 있는 맨드렐의 크기에 따른 처짐량을 계산하기 위해 식 (1)을 이용하고 강재의 밀도와 탄성계수는 각각 7.85 g/cm³, 210 GPa을 적용하였다. 맨드렐 길이는 5,000 mm로 고정하고, 튜브의 외경이 다를 때 각각의 처짐량을 비교한 결과를 Fig. 6에 나타내었으며, 직경이 클수록 처짐량은 감소함을 볼 수 있다.

Fig. 6

Maximum deflection of a tube-section mandrel with various diameters (Length: 5,000 mm)

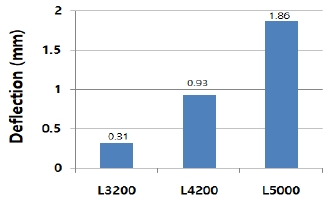
튜브 맨드렐의 외경을 일정하게 하고 길이를 변화시킬 때의 처짐량 변화를 Fig. 7에 보이고 있다. 길이가 길수록 처짐량이 증가함을 볼 수 있으며, Fig. 6의 직경 100 mm와 비교하면 같은 길이일 때, 직경이 클수록 처짐량이 적음을 알수 있다.

Fig. 7

Maximum deflection of a tube-section mandrel with various length (Diameter: 80 mm)

4. 복합재료 기본물성치 시험

최적의 섬유 적층 각도를 구하기 위한 복합재 튜브 구조물 해석에서, 재료 물성에 대한 입력값으로 일방향 복합재료에 대한 물성치가 필요하다. 사용 섬유뿐만 아니라 시편의 제조 방법에 따라 물성치의 변화가 크기 때문에 본 연구에서는, 해석의 정확도와 신뢰도를 높이기 위해 복합재 튜브를 제조하는 방법과 동일하게 평판을 제조하여 기계적 시험을 하였다.

사용 섬유는 TORAY 사의 탄소섬유인 T700SC-24000-50C이며, 수지는 국도화학의 에폭시를 사용하였다. Fig. 8에 보는 바와 같이 필라멘트 와인딩 공정으로 평판을 제작한 후 오븐 내에서 90℃에서 2시간 동안 경화하였다. Fig. 9는 경화 후의 복합재 평판을 보인 것이다.

Fig. 8

Winding of a UD composite plate

Fig. 9

UD composite plate for test specimen

복합재 구조 설계를 위한 기본적인 기계적 물성치는 인장, 압축, 면내전단에 대한 탄성계수 및 강도값이며 시험규격은 Table 3에 나와 있다. 섬유체적율은 58.9%이었다.

Table 3

Standard test specification

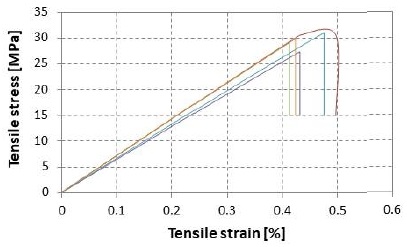
Fig. 10 및 Fig. 11은 일방향 복합재료 시편의 0° 방향과 90° 방향의 응력-변형률 곡선을 대표적으로 보인 것이다. 이 그림에서 표시한 곡선은 각 5개의 시편에 대한 결과이다.

Fig. 10

Tensile stress-strain of 0° specimen

Fig. 11

Tensile stress-strain of 90° specimen

Table 4는 일방향 복합재료 기계적 특성시험 결과를 정리한 것으로 각 값의 괄호 안의 숫자는 표준편차를 보인 것이다.

Table 4

Mechanical properties of UD composites

5. 복합재 튜브 설계

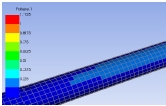
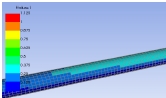
복합재 튜브의 기계적인 특성을 가장 크게 좌우하는 것은 섬유가 와인딩되는 적층 각도이다. 냉각탑의 복합재 튜브에 적용하는 각도는 헬리컬 와인딩과 후프 와인딩을 혼합한 [±θ/90/±θ/±15/90]를 고려하였으며, 헬리컬 각도 θ의 변화에 따른 복합재 튜브의 구조 강도를 해석하였다. 복합재 튜브 모델링은 ANSYS Workbench 2020 R2의 적층복합재료 모델링 툴인 ACP를 사용하였다, 각도별로 세 종류의 복합재 튜브 (θ = 15°, 30°, 45°)에 대한 모델링을 수행하였다. 튜브의 구속조건은 일단고정-타단지지 조건을 사용하였으며, 정중앙에는 1,000 N의 하중을 가하여 θ의 변화에 따른 처짐량과 파손 여부를 확인하였다. 이 하중은 복합재 튜브가 설치되거나 운용 중, 사람이나 물체가 올라가 있는 상황을 가정한 것이다.

적층복합재료의 파손여부를 확인할 때 파손기준은 금속에도 사용하는 Max. stress, Max. strain 기준과 복합재료의 기준인 Tsai-Wu 및 Tsai-Hill theory를 적용하였으며, 이 중 어느 하나라도 파손지수가 1을 넘으면 파손되는 것으로 가정하였다.

1,000 N이 작용할 때 적층패턴별 처짐량과 파손지수 결과가 Table 5에 나와 있다. θ가 증가함에 따라 처짐량과 파손지수도 증가하였다. 그러나 이 하중에서는 최대 파손지수가 0.38이므로 세 종류의 적층패턴 모두 안전하며 θ=15°의 경우가 가장 안전한 것으로 평가된다.

Table 5

Comparison of deflection and failure index for three cases of stacking sequences.

6. 복합재 튜브제조 및 치수검사

사용한 맨드렐은 길이 5,000 mm, 외경 100 mm, 내경 80 mm인 강재 튜브이다, 적층 각도는 [±15/90/±15/±15/90] 로서 총 8 ply를 적층하였으며 90° 층이 외부층이다. 와인딩이 완료된 후 맨드렐과 적층재료는 오븐에 넣어 전체를 회전시키면서 90℃에서 2시간 동안 경화하였다. 경화 후 상온까지 냉각시킨 후 복합재를 맨드렐에서 제거하여 탈형하였다. Fig. 12는 필라멘트 와인딩 기계에서 맨드렐에 수지함침된 탄소섬유가 와인딩되는 모습을 보인 것이다.

Fig. 12

Filament winding of a composite pipe

Fig. 13은 드렐에서 탈형한 후 기계 가공한 복합재 튜브를 보인 것이며 크기는 길이 3,300 mm, 내경 100 mm, 외경 107 mm이다.

Fig. 13

Composites pipes.

맨드렐의 처짐에 따른 복합재의 굽힘변형을 확인하기 위하여 튜브 5개에 대하여 다이얼 게이지를 사용하여 측정하였다. 튜브제조에 사용한 맨드렐은 길이 5,000 mm, 외경 100 mm, 내경 80 mm 이다(Table 1 참고). 맨드렐의 처짐량은 Fig. 6 D10의 결과에 보인 바와 같이 1.21 mm로 예측되었으나 경화 후 복합재 파이프의 변형량은 길이 방향의 직진도에서 평균 1.546 mm로 측정되어 약 22%의 오차를 보여 주고 있다. Table 6에 측정 결과와 예측치를 요약하였다. 맨드렐의 처짐량 예측에 비해 복합재의 변형량이 크게 나타난 이유는 복합재의 경화 중 가해진 열에 의하여 경화 후 잔류응력이 발생하여 실제보다 더 큰 굽힘이 발생하였기 때문으로 판단된다.

Table 6

Comparison of deflection results between composites pipe and mandrel (Unit, mm)

7. 결 론

와인딩 멘드렐 설계, 최적의 적층각도 설계를 위한 구조해석, 필라멘트 와인딩 공정 등의 과정을 통하여 냉각탑용 복합재 튜브 (길이 3,300 mm, 내경 100 mm, 두께 3.5 mm)를 제조하였다.

1) 맨드렐 설계에서는 복합재료 튜브의 굴곡 변형을 최소로 하기 위한 맨드렐의 단면형상, 직경 및 길이의 영향을 확인하였으며, 치수 정밀도를 유지하기 위해서는 튜브형 맨드렐을 사용하는 것이 필요하다.

2) 다양한 적층 각도에 대한 구조 강도해석을 하였으며, 파이프의 기계적 성능과 와인딩 용이성을 고려하여 최적의 헬리컬 와인딩 각도는 15°였으며, 적층순서는 [±15/90/±15/±15/90]로서 총 8 ply를 적층하여 복합재 파이프를 제조하였다.

3) 맨드렐의 처짐에 따른 복합재의 굽힘 변형을 측정하여 예측치와 비교하였다. 파이프의 변형량은 평균 1.546 mm이었으며 예측치와 약 22%의 오차를 보였다.

Author contributions

B. H. Kim; Investigation, Conceptualization, Supervision, Writing-original draft. T. Y. Kim; Fabrication, Methodology, Formal analysis. J. I. Yoon; Project adminstration, Writing-review & editing.

References

• C. K. Moon, Y. M. Choi, D. Y. Kim and B. A. Kim, 2020, “A Study on the Mechanical Properties of Epoxy Composites Using Carbonnanotube”, Journal of Power System Engineering, 24(4), 5-10. [https://doi.org/10.9726/kspse.2020.24.4.005]
• B. S. Kim, B. H. Kim and J. B. Kim, 2004, “Composite Pressure Vessel for Natural Gas Vehicle by Filament Winding”, Composites Research, 17(5), 1-6.
• Y. G. Lee, J. S. Park, S. H. Kim, H. L. Kim, and S. J. Yoon, 2013, “Compression Behavior of Manufacturability Enhanced FRP-Concrete Hybrid Composite Pile”, Composites Research, 26(1), 66-71. [https://doi.org/10.7234/kscm.2013.26.1.66]
• S. J. Lim, C. D. Kong and H. B. Park, 2012, “A Study on Optimmal Design of Filament Winding Composite Tower for 2MW Class Horizontal Axis Wind Turbine Systems”, Composites Research, 25(2), 54-61. [https://doi.org/10.7234/kscm.2012.25.2.054]
• T. K. Hwang, J. B. Park, H. G. Kim, Y. D. Doh and S. I. Moon, 2007, “Dome Shape Design and Performance Evaluation of Composite Pressure Vessel”, Composites Research, 20(4), 31-41. [https://doi.org/10.7234/kscm.2007.20.4.031]
• I. H. Cho, J. S. Park and S. H. Oh, 2003, “Development of Payload Kick Motor for KSR-Ⅲ Ⅰ. Design of Downscaled Structure & Processing Method”, Composites Research, 16(2), 1-8.
• H. Herna´ndez-Moreno, B. Douchin, F. Collombet, D. Choqueuse and P. Davies, 2008, “Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure”, Composites Science and Technology, 68, 1015-1024. [https://doi.org/10.1016/j.compscitech.2007.07.020]
• A. R. Abu Talib, A. Ali, M. A. Badie, N. A. C. Lah and A. F. Golestaneh, 2010, “Developing a hybrid, carbon/glass fiber reinforced, epoxy composite automotive drive shaft”, Materials Design, 31, 514-521. [https://doi.org/10.1016/j.matdes.2009.06.015]
• M. A. Badie, E. Mahdi and A. M. S. Hamouda, 2011, “An investigation into hybrid carbon/glass fiber reinforced epoxy composite automotive drive shaft”, Materials Design, 32, 1485-1500. [https://doi.org/10.1016/j.matdes.2010.08.042]
• B. Gireesh, B. S. Shrishaliand, V. N. Satwik, 2013, “Finite element and experimental investigation of composite torsion shaft”, International Journal of Engineering Research and Application, 3, 1510-1517.
• C. Colombo and L. Vergani, 2018, “Optimization of filament winding parameters for the design of a composite pipe”, Composites Part B Engineering, 148, 207-216. [https://doi.org/10.1016/j.compositesb.2018.04.056]