The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 27, No. 3, pp.28-39

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 30 Jun 2023

Received 17 Feb 2023 Revised 24 Jun 2023 Accepted 26 Jun 2023

DOI: https://doi.org/10.9726/kspse.2023.27.3.028

케이블을 이용한 무인비행체 운송시스템의 화물 거동 안정화 제어계 설계에 관한 연구

임재준^*

; 조경진^**

; 이동훈^***^{, †}

*연구원, 부경대학교 산업과학기술연구소
**대표, 주식회사 물과공기
***조교수, 부경대학교 기계시스템공학전공

A Study on Control System Design Method for Payload Stabilization of a UAV with Suspended Payload

Jae-Jun Lim^*

; Kyung-Jin Cho^**

; Dong-Hun Lee^***^{, †}

*Researcher, The Industrial Science Technology Research Center, Pukyong National University.
**CEO, Water & Air Co. Ltd.
***Assistant Professor, Department of Mechanical System Engineering, Pukyong National University.

Correspondence to: ^†Dong-Hun Lee : Assistant Professor, Department of Mechanical System Engineering, Pukyong National University. E-mail : hun_control@pknu.ac.kr, Tel : 051-629-6191

초록

본 논문에서는 운송용 무인비행체(UAV)의 화물 운송작업 중 발생하는 화물 흔들림 억제를 위한 비행 및 윈치 제어전략에 대해 다룬다. 예를 들어, 해상 영역에서 화물운송 하는 경우 해상환경의 악조건으로 안정적인 작업을 수행하는데 많은 어려움이 있다. UAV가 선박에 착륙할 수 있는 공간이 매우 협소하고 갑판에 설치된 수많은 와이어와 충돌 가능성이 있으므로 공중에서 와이어를 통해 하역하는 과정으로 배송하는 방법이 유일하다. 그러나 와이어를 통해 화물을 하역하는 경우 강한 해상 바람으로 인해 화물 거동이 불안정해지며 결국 목표지점에 안착시키기 어려워지게 된다. 따라서 본 논문에서는 와이어 길이 능동 제어를 통한 화물 거동 안정화 제어기 설계법을 제안한다. 또한 설계한 제어기의 우수성을 평가하기 위하여 위치 보상기, 와이어 길이 능동 제어를 고려하지 않은 비선형 제어기를 적용한 경우와 제어성능을 비교한다. 마지막으로 시뮬레이션을 통해 본 논문에서 제안하는 제어기 설계법의 유효성을 검증한다.

Abstract

In this paper, we propose a payload stabilization control design method for a UAV with a suspended payload for transporting. The primary problem that arises from cargo transporting with a UAV, is that of safe unloading in harsh environmental conditions. In this paper, the possible superior control system configurations are discussed to show the advantages of actively controlling the cable length. Therefore, we propose a nonlinear control system with active control of the winch. To evaluate the control performance of the proposed control system, along with a simple position compensator and nonlinear control system with constant cable length, a comparison study is also conducted. The control performance and efficiency of the proposed control system are validated through simulation on a UAV model.

Keywords:

UAV (Unmanned Aerial Vehicle), Suspended Payload Stabilization, Integral Sliding Mode Control, Adaptive Control, Actively Controlled Wire Length

키워드:

무인비행체, 화물 안정화, 적분형 슬라이딩모드제어, 적응제어, 능동 와이어

1. 서 론

본 논문에서는 운송용 무인비행체(UAV)의 화물 운송작업 중 발생하는 화물 흔들림 억제를 위한 비행 및 윈치 제어전략에 대해 고찰한다.

최근 UAV 공공, 민간 등 다양한 활용산업이 형성되어 사회 및 경제적으로 영향력이 큰 기술로 분류되고 있다. 특히, 해외의 경우 아마존(Aazon), UPS(United Parcel Service), 구글(Google), 라쿠텐 (Rakuten) 등이 도서·산간오지를 대상으로 화물운송 작업을 수행하고 있으며,¹⁾ UAV가 주택 마당과 같은 목표지점에 착륙하여 화물을 내려놓거나 호버링(hovering) 상태에서 윈치를 이용하여 화물을 하역하는 방법으로 운송하고 있다.

국내의 경우, 77% 이상이 아파트 등의 공동주택에 거주하고 있어 UAV가 착륙하여 화물을 전달하기 어렵기 때문에 착륙 없이 윈치를 이용하여 화물을 하역하는 것이 적합하다. 또한 국내에서 운영 중인 계류 선박을 대상으로 UAV를 활용한 배송 서비스의 경우에도 선박에 착륙할 수 있는 공간이 매우 협소하고 갑판에 설치된 수많은 와이어와 충돌 가능성이 있으므로 호버링 상태에서 윈치를 이용하여 화물을 하역하는 방식으로 배송 서비스를 운영하고 있다.^2-3) 하지만 와이어를 통해 화물을 하역하는 경우, 강한 바람과 같은 외부 요인에 의해 화물 거동이 불안정해지면 목표지점에 하역하기 어려우며, 예상보다 긴 비행시간이나 기체 안정성 악화로 충돌, 추락과 같은 사고로 이어질 수 있다.

이와 같이 환경적 요인과 모델 불확실성 등 악조건에서도 안정적인 비행과 화물 이송을 위해 다양한 연구가 진행되고 있다. T. Chen 등은 기구적으로 한계점을 극복하기 위해 4개 와이어를 기체와 화물에 병렬로 연결하여 횡운동을 억제하고자 하였다.⁴⁾ 또한 소형 단일 및 다중 UAV를 활용한 화물 운송의 경우 단순화된 동적 모델을 사용하여 UAV와 화물 사이의 동적결합을 고려하지 않고 있다.^5-7) 또한 S. Dai 등은 UAV, 와이어 및 화물을 고려한 모델링을 수행하였고 유연한 와이어 구현을 위해 n개의 다중 강체 링크로 고려하여 UAV의 PD 위치 및 자세 제어기를 통해 횡운동을 억제하였다.⁸⁾ 이와 같이 대부분 연구는 와이어 길이를 고려하지 않고 화물의 횡운동 억제를 위하여 제어기법, 경로 생성 등 무인비행체 비행제어 관점에서만 문제를 다루고 있다.^9-13) 그러나 배송지 상황에 따라 화물을 윈치로 올리거나 내려야하는 경우 UAV와 화물 거동이 불안정해질 수 있으므로 이에 대한 안정성 평가가 필요하다. 이를 위하여 Y. Yang 등의 연구에서는 와이어 길이가 등속으로 변하는 환경 즉, 화물을 등속으로 하역하는 상황을 고려하였다.¹⁴⁾ 그러나 와이어 길이 변화를 외란으로 고려하여 화물 거동을 억제하고자 하였으나 비행제어 관점에서만 접근한 것이다.

그러나 많은 분야에 잘 알려진 것과 같이 와이어 길이를 제어변수로 두고 능동 제어를 수행하는 경우 횡운동 억제 문제를 해결할 수 있다. 예를 들어 X. Li 등의 연구에서는 선박 크레인을 이용한 하역 작업에서 발생하는 화물 횡운동이 와이어 길이 제어를 통해 억제될 수 있음을 제시하였다.¹⁵⁾ 여기서 알 수 있듯이 와이어 능동 제어를 통해 기존 비행제어 관점에서 수행된 선행연구의 제어성능을 향상시킬 수 있다.

따라서 본 논문에서는 와이어 길이를 제어변수로 고려한 화물 거동 안정화 제어시스템 설계법을 제안한다. 먼저, 와이어 길이를 상태변수 고려한 제어대상 모델식을 이용하여 UAV 위치 및 자세 PD제어기를 설계한다. 그리고 화물 거동 안정화 제어기를 설계하여 UAV 위치 및 자세 PD제어기 제어입력의 기준신호와 결합한 형태의 제어시스템을 설계한다.

특히, 제어성능 비교평가를 통해 제안하는 제어시스템 설계법의 유효성을 검증하기 위하여 설계 과정이 단순한 위치 보상기, 외란에 대한 강인성과 우수한 제어성능 확보를 위한 적응형 적분슬라이딩모드 기반 화물 거동 안정화 제어기와 윈치 능동제어를 고려한 적응형 적분슬라이딩모드 제어기를 설계한다. 마지막으로 시뮬레이션을 통해 설계한 제어시스템의 유효성을 검증하고 제어성능 비교평가를 수행한다.

2. 시스템 모델링

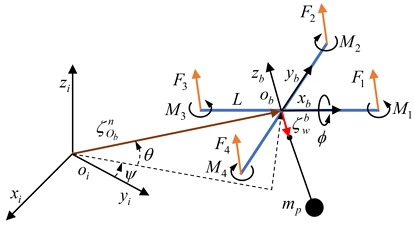
본 논문에서는 Fig. 1에 나타낸 것과 같이 제어대상인 해상운송용 UAV가 이에 매달린 화물을 이송하는 상황을 고려한다.

Fig. 1

Quadrotor suspended payload system

또한 시스템 운동방정식을 유도하기 위해 지구중심관성좌표계(i-frame, o_i,x_i,y_i,z_i)와 물체고정좌표계(b-frame, o_b,x_b,y_b,z_b)를 도입하였으며, 모델링 간소화를 위해 다음과 같은 가정을 둔다.

1) UAV는 강체이고 대칭이다.
2) 화물의 횡운동은 UAV 운동에 영향을 미치지 않을 정도로 작다.
3) 화물은 질점으로 고려하고, 와이어의 질량 무시할 만큼 작다.
4) 와이어 동특성은 무시할 만큼 작다.
5) b-frame 원점과 UAV 무게중심은 일치한다.

이에 따라 Fig. 1에 나타낸 제어대상 시스템에 대하여 l은 와이어 길이, m_p는 화물 질량, F_i (i=1,...,4)는 각 로터의 추력, M_i (i=1,...,4)는 블레이드 회전 모멘트, L은 쿼드로터 무게중심으로부터 로터 중심까지의 수평거리, $ζ O b n$ 는 b-frame에 대한 i-frame의 벡터를 나타낸다. 그리고 i-frame에서 정의되는 UAV의 위치 및 자세벡터는 각각 $η o b i = x y z T$ , $Θ = ϕ θ ψ T$ 이며, b-frame에서의 선속도와 각속도 벡터는 $v o b = u v w T$ , $ω o b = p q r T$ 으로 나타낼 수 있다.

와이어 끝단에 고정된 화물은 Fig. 2와 같이 3차원 공간상 운동으로 표현할 수 있다. 여기서, α는 y_i축 방향에 대한 화물 회전각도, β는 x_i축 방향에 대한 화물 회전각도를 의미한다.

Fig. 2

Motion of a suspended payload in three-dimensional space

여기서, i-frame에서 정의되는 화물의 좌표는 다음과 같이 UAV의 무게중심 위치벡터, b-frame 원점으로부터 윈치에 대한 벡터, 윈치로부터 화물에 대한 벡터로 표현할 수 있다.

η p i = η o b i + R b i ζ w b + ζ p i

(1)

여기서, $ζ w b = x w y w z w T$ 는 UAV 무게중심으로부터 윈치에 대한 벡터를 나타내며, $R b i$ 는 회전행렬을 의미한다.

R b i = c θ c ψ - s ψ c ϕ + c ψ s θ s ϕ s ψ s ϕ + c ψ c ϕ s θ s ψ c θ c ψ c ϕ + s ϕ s θ s ψ - c ψ s ϕ + s θ s ψ c ϕ - s θ c θ s ϕ c θ c ϕ

(2)

여기서, c(•) ≡ cos(•), s(•) ≡ sin(•)로 나타낸다. 또한 와이어 길이를 l이라 둔다면 윈치로부터 화물에 대한 벡터는 다음과 같이 정의된다.

ζ p i = l s i n α l cos α sin β - l cos α cos β T

(3)

UAV 운동과 이에 매달린 화물의 횡운동을 고려한 대상시스템의 전체 운동방정식은 일반화 좌표를 $q = η o b i T Θ T α β l T$ 으로 정의하고 식 (4) 라그랑주 방정식(Lagrange’s equation)을 통해 도출할 수 있다.²⁾

d d t ∂ T ∂ q ˙ i - ∂ T ∂ q i + ∂ U ∂ q i = Q i

(4)

여기서, T는 대상시스템의 운동에너지, U는 위치에너지, Q_i는 일반화 외력을 나타낸다. 앞서 기술한 가정에 따라 운동에너지¹⁶⁾와 위치에너지를 다음과 같이 둘 수 있다.

T = 12 m p η ˙ p i T η ˙ p i + m q η ˙ o b i T η ˙ o b i + ω o b T I q ω o b

(5)

U = g m p η p, z i + g m q η o b, z i

(6)

여기서, m_q는 UAV 질량, I_q = diag[I_xx, I_yy, I_zz]는 UAV 관성행렬, g는 중력가속도를 나타낸다.

식 (4) 라그랑주 방정식에 식 (5)와 식 (6)을 대입하여 전개하면 UAV 운동방정식과 화물 운동방정식을 도출할 수 있다. 즉, UAV와 화물의 운동특성과 상관관계를 해석할 수 있다. 먼저 화물 운동방정식은 UAV 운동을 외력으로 하는 식 (8)~(10)으로 나타내어진다.

l 2 m p α ¨ + 2 α ˙ l ˙ l m p + β ˙ 2 l 2 m p c o s ⁡ α s i n ⁡ α + g l m p c o s ⁡ β s i n ⁡ α = Q α - x ¨ l m p c o s ⁡ α + y ¨ l m p s i n ⁡ α s i n ⁡ β - z l ¨ l m p c o s ⁡ β s i n ⁡ α

(8)

l 2 m p c o s 2 ⁡ α β ¨ + 2 β ˙ l ˙ l m p c o s 2 ⁡ α - α ˙ β ˙ l 2 m p s i n ⁡ 2 α + g l m p c o s ⁡ α s i n ⁡ β = Q β - y ¨ l m p c o s ⁡ α c o s ⁡ β - z ¨ l m p c o s ⁡ β s i n ⁡ α

(9)

m p l ¨ - α ˙ 2 l m p - β ˙ 2 l m p c o s 2 ⁡ α - g m p c o s ⁡ α c o s ⁡ β = Q l - x ¨ m p s i n ⁡ α - y ¨ m p c o s ⁡ α s i n ⁡ β + z ¨ m p c o s ⁡ α s i n ⁡ β

(10)

여기서, Q_α과 Q_β는 각각 x_i축, y_i축 방향으로 화물에 작용하는 항력이나 바람으로 인한 외력, Q_l은 와이어에 작용하는 장력으로 고려할 수 있다.

UAV 운동방정식은 가정2)를 적용하여 화물 횡운동으로 인한 UAV 운동 변화를 무시한다면 간소화된 UAV 운동방정식¹⁷⁾ 식 (11)과 식 (12)로 정리된다.

m q η ¨ o b i = 00 - m q g + R b i 00 F 1 + F 2 + F 3 + F 4

(11)

I q p ˙ q ˙ r ˙ = L F 2 - F 4 L F 3 - F 1 M 2 + M 4 - M 1 - M 3 - p q r × I q p q r

(12)

3. 제어기 설계

3장에서는 앞서 도출한 제어대상 모델을 이용하여 화물 거동 안정화 제어기 설계법을 제안한다. 특히, 본 논문에서는 PD제어 기반 UAV 비행제어기를 먼저 설계한 후 3.2에서 설계한 화물 거동 안정화 제어기와 결합한 형태의 제어시스템을 설계한다.

3.1 UAV 위치 및 자세 PD제어

UAV 운동방정식은 식 (11)과 식 (12)에 나타내었으며, 이를 이용하여 표현의 간소화를 위해 추력 및 토크 벡터를 다음과 같이 나타낸다.

F 1 + F 2 + F 3 + F 4 = u 1

(13)

L F 2 - F 4 L F 3 - F 1 M 2 + M 4 - M 1 - M 3 = u 2

(14)

i-frame에서 표현되는 UAV 위치오차 및 속도오차를 다음과 같이 둔다.

e p = η d i - η o b i, e v = η ˙ d i - η ˙ o b i

(15)

여기서, $η d i = x d e s y d e s z d e s T$ 는 UAV의 기준 경로를 나타낸다.

UAV 위치 기준신호를 $η c i = x c y c z c T$ 으로 정의한다면, 다음 식을 만족시키는 위치제어기 설계 문제로 정리할 수 있다.

η ¨ d i - η ¨ c i + K d η ˙ d i - η ˙ o b i + K p η d i - η o b i = 0

(16)

여기서, $K d ∈ R 3 × 3 > 0$ , $K p ∈ R 3 × 3 > 0$ 는 각각 위치제어기 이득을 나타낸다. 즉, 식 (16)를 $η ¨ c i$ 에 대해 다시 정리하면 제어출력을 $η ¨ c i$ 으로 하는 위치제어기가 된다.

또한 식 (11)을 선형화하고 가속도 및 자세를 기준신호로 변경하면 i-frame에서 정의되는 자세벡터의 기준신호 $Θ c = ϕ c θ c ψ c T$ 를 계산할 수 있다. 그리고 Θ와 $ω o b$ 의 관계식 $ω o, c b = W v Θ Θ ˙ c$ 에 따라 b-frame에서 정의되는 각속도 벡터의 기준신호 $ω o, c b = p c q c r c T$ 를 구할 수 있다. 이를 식 (17)과 식 (18)에 정리하였다.

ϕ c = 1 g x ¨ c sin ⁡ ψ d e s - y ¨ c cos ⁡ ψ d e s θ c = 1 g x ¨ c cos ⁡ ψ d e s + y ¨ c sin ⁡ ψ d e s ψ c = ψ d e s z ¨ c = z ¨ d e s + K d, 3 z ˙ c - z ˙ + K p, 3 z c - z

(17)

p c q c r c = 10 - s i n ⁡ θ 0 c o s ⁡ ϕ c o s ⁡ θ s i n ⁡ ϕ 0 - s i n ⁡ ϕ c o s ⁡ θ c o s ⁡ ϕ ⏟ W v Θ ϕ ˙ c θ ˙ c ψ ˙ c

(18)

결국 PD기반 위치 및 자세 제어기의 추력과 토크 벡터는 다음과 같이 설계된다.

u 1 = m g + z ¨ c u 2 = I K p Θ c - Θ + K d ω o, c b - ω o b

(19)

여기서, u₁과 u₂는 식 (13)과 식 (14)에 나타내었듯이 각각 추력 및 롤링(rolling), 피칭(pitching), 요잉(yawing) 모멘트 제어입력을 의미한다.

3.2 화물 거동 안정화 제어기

3.2.1 화물 거동 안정화 위치 보상기

첫 번째 제안하는 제어계 설계법은 x_iy_i 평면에서 발생하는 UAV 위치와 화물의 위치오차를 보상하는 방법이다.

식 (8)~(10)에서 확인할 수 있듯이 벡터 $ζ w b$ 는 화물 횡운동 α, β에 관여하지 않으며 그 값이 미소하여 좌표에서 무시할 수 있다면 $ζ w b = 0$ 으로 둘 수 있다. 그리고 i-frame에서 정의되는 화물 좌표는 식 (4)에 따라 다음과 같이 정리된다.

η p i = x p i y p i z p i = x + l s i n ⁡ α y + l c o s ⁡ α s i n ⁡ β z - l c o s ⁡ α c o s ⁡ β

(20)

식 (20)을 이용하여 α, β에 대해 정리하면 다음과 같다.

α = s i n - 1 ⁡ x p i - x l, β = s i n - 1 ⁡ y p i - y l c o s ⁡ α

(21)

식 (20)과 식 (21)에 따르면, 화물 거동 안정화를 달성하는 것은 α→0, β→0 즉, UAV가 화물 동요를 오차 없이 추종( $x → x p i$ , $y → y p i$ )해야 함을 알 수 있다. 따라서 다음과 같은 위치 보상기를 UAV의 위치 기준 경로를 다음과 같이 새롭게 정의함으로써 설계할 수 있다.

η d i = x d e s y d e s z d e s + l s i n ⁡ α l c o s ⁡ α s i n ⁡ β l 1 - c o s ⁡ α c o s ⁡ β

(22)

3.2.2 적응형 적분슬라이딩모드 제어

앞서 설계한 위치 보상기는 화물 거동에 대한 동특성이 고려되지 않았으므로 안정성과 성능을 보장할 수 없다. 따라서 제안하는 두 번째 제어계 설계법은 화물 거동 동특성을 반영한 강인 제어기 설계법을 제안한다. 특히, 화물에 작용하는 항력이나 바람 등 불확실성에 대응하기 위해 적응 법칙을 사용하여 추종 성능 향상을 시도한다.

제어기 설계를 위해 ν = [αβ]^T로 정의하면, 식 (8)과 (9)를 다음과 같이 정리할 수 있다.

M 1 ν ν ¨ + C 1 ν, ν ˙ ν ˙ + H 1 ν = B 1 ν U 1 + Q 1 ν

(23)

M 1 ν = l 2 m p 0 0 l 2 m p c o s 2 ⁡ α C 1 ν, ν ˙ = 2 l l ˙ m p β ˙ l 2 m p c o s ⁡ α s i n ⁡ α - β ˙ l 2 m p s i n ⁡ 2 α 2 l l ˙ m p c o s 2 ⁡ α H 1 ν = g l m p c o s ⁡ β s i n ⁡ α g l m p c o s ⁡ α s i n ⁡ β B 1 ν = - l m p c o s ⁡ α - l m p s i n ⁡ α s i n ⁡ β l m p c o s ⁡ β s i n ⁡ α 0 l m p c o s ⁡ α c o s ⁡ β l m p c o s ⁡ α s i n ⁡ β U 1 = x ¨ c y ¨ c z c ¨, Q 1 ν = Q α Q β

여기서, $x ¨ c$ , $y ¨ c$ , $z ¨ c$ 는 UAV 자세제어기 입력신호를 나타낸다.

적응형 적분슬라이딩모드 제어기(adaptive integral sliding mode controller) 설계를 위하여 화물 회전각도 α, β의 기준값을 ν_d = [α_dβ_d]^T = [00]^T, 상태오차를 e₁ = ν_d - ν으로 정의하고 적분기를 도입한 슬라이딩 평면을 다음과 같이 둔다.

σ 1 = e ˙ 1 + ϵ 1 e 1 + ϵ 2 ∫ 0 t e 1 d τ

(24)

여기서, $ϵ 1, ϵ 2 ∈ R 2 × 2 > 0$ 이다. 위 식 (24)를 이용하여 적응형 적분슬라이딩모드 제어기를 다음과 같이 설계한다.

U 1 = U 1, I S M C + U 1, a d a p t i v e

(25)

U 1, I S M C = B 1 * ν C 1 ν, ν ˙ ν ˙ + H 1 ν + ⋯ M 1 ν ϵ 1 e ˙ 1 + ϵ 2 e 1 + K 1 s g n ⁡ σ 1 U 1, a d a p t i v e = - B 1 * ν Q^1 ν

여기서, $K 1 ∈ R 2 × 2 > 0$ , $B 1 * ν$ 는 $B 1 ν$ 의 pseudo 역행렬을 의미한다.

B 1 * ν = B 1 T ν B 1 ν B 1 T ν - 1

(26)

위 식에서 $B 1 ν B 1 T ν - 1$ 가 정칙(nonsingular)이어야 하므로 일반적으로 상태벡터 ν에 대한 제약조건(α ≠ ±π/2)이 주어지지만 본 논문에서는 제어대상의 상태벡터 ν를 좁은 범위에서 고려하고 있으므로 정칙을 만족시킨다.

설계한 제어기의 안정성 평가를 위해 리아푸노프 함수 식 (27)을 도입한다.

V 1 = 12 σ 1 T σ 1 + 1 2 λ 1 Q ~ 1 T Q ~ 1

(27)

여기서, $Q ~ 1 = Q 1 - Q^1$ , λ₁ > 0이며, 외력 변화속도가 충분히 느리다면 $Q ˙ 1 = 0$ 으로 둘 수 있다. 식 (27)의 시간 도함수에 식 (25)를 대입하여 정리하면 다음과 같다.

V ˙ 1 = σ T σ ˙ + 1 λ 1 Q ~ 1 T Q ~ 1 ˙ = σ T ϵ 1 e ˙ 1 + ϵ 2 e 2 + M 1 ν - 1 … C 1 ν, ν ˙ ν ˙ + H 1 ν - B 1 ν U 1 - Q 1 ν … + 1 λ 1 Q ~ 1 T Q ~ ˙ = - σ T K 1 s g n ⁡ σ 1 + M 1 ν - 1 Q ~ 1 + 1 λ 1 Q ~ 1 T Q 1 ˙

(28)

위 식 (28)에 대하여 업데이트 식 (29)를 갖는다면 $V ˙ 1 = - K 1 σ ≤ 0$ , $V ¨ = K 12$ 이므로 Barbalat’s lemma¹¹⁾에 따라 t→∞에 대해 $σ → 0, Q ~ 1 → 0$ , 즉 안정성을 확보할 수 있다.

Q^˙ 1 = - λ 1 M 1 ν - 1 σ 1

(29)

설계한 제어기 식 (25)을 식 (17)과 식 (18)에 적용하면 새로운 자세 기준신호( $ϕ - c 1, θ - c 1, ψ - c 1$ )와 ( $p - c 1, q - c 1, r - c 1$ )를 계산할 수 있다. 이를 UAV 위치 및 자세제어기 제어입력의 기준신호와 합을 구함으로써 화물 거동 억제 제어기를 반영한 UAV 제어시스템을 구축할 수 있다. 즉, 식 (19)의 기준신호는 다음과 같이 정리된다.

Θ c = ϕ c θ c ψ c + ϕ - c 1 θ - c 1 ψ - c 1, ω o, c b = p c q c r c + p - c 1 q - c 1 r - c 1

(30)

3.2.3 능동 윈치기반 적응형 적분슬라이딩모드 제어

앞서 설계한 적응형 적분슬라이딩모드 제어는 상태 α, β를 제어변수로 설정하고 제어목적을 달성하고자 하였다. 그러나 기존 많은 연구에서 알려진 것과 같이 와이어 길이를 제어변수로 설정하고 화물 거동 안정화 제어목적을 달성할 수 있다. 따라서 본 논문에서 새롭게 제안하는 제어계 설계법은 상태변수를 다음과 같이 정의한다.

μ = α β l

(31)

여기서, l은 와이어 길이를 나타낸다. 따라서 능동 윈치기반 적응형 적분슬라이딩모드 제어는 α→0, β→0, l→l_d를 제어목적으로 한다. 이를 달성하기 위하여 윈치 운동방정식을 식 (32)로 둔다.

J w l ¨ w + C w l ˙ w + K w l w = r w T w u w - Q l

(32)

J_w는 윈치 드럼 질량관성모멘트 상수, C_w는 윈치 감쇠계수, K_w는 윈치 강성계수, T_w는 제어입력 이득을 나타낸다. 그리고 l(t)=l(0)+l_w(t) 관계를 갖는다.

식 (10)을 $z ¨$ 에 대해 정리하여 식 (8)과 식 (9)에 대입하고, 식 (32)를 이용하면 식 (8)~(10)을 다음과 같이 다시 나타낼 수 있다.

M 2 μ μ ¨ + C 2 μ, μ ˙ μ ˙ + H 2 μ … = B 2 μ U 2 + Q 2 μ

(33)

M 2 μ = l 2 m p 0 m p t a n ⁡ α 0 l 2 m p c o s 2 ⁡ α m p t a n ⁡ β 00 m p + J w, C 2 μ, μ ˙ = C 2 1,1 C 2 1, 2 α ˙ l m p C 2 2, 1 C 2 2, 2 β ˙ l m p c o s 2 ⁡ α 00 C w, H 2 μ = (l - 1) g m p c o s ⁡ β s i n ⁡ α (l - 1) g m p c o s ⁡ α s i n ⁡ β - g m p c o s ⁡ α c o s ⁡ β + K w l + x ¨ m p s i n ⁡ α ⋯ + y ¨ m p c o s ⁡ α s i n ⁡ β - z m ¨ p c o s ⁡ α c o s ⁡ β ⋯ - α ˙ 2 l m p - β ˙ 2 l m p c o s 2 ⁡ α - g m p c o s ⁡ α c o s ⁡ β B 2 μ = B 2 1,1 B 2 1, 2 - T ω t a n ⁡ α B 2 2, 1 B 2 2, 2 - T ω t a n ⁡ β 00 - T ω U 2 = x ¨ c y ¨ c u w, Q 2 μ = Q α Q β 0, C 2 1,1 = l ˙ l m p - α ˙ l m p t a n ⁡ α, C 2 2, 1 = - β ˙ l 2 m p s i n ⁡ 2 α - α ˙ l m p t a n ⁡ β, C 2 1, 2 = l - 1 β ˙ l m p c o s ⁡ α s i n ⁡ α, C 2 2, 1 = l ˙ - β ˙ t a n ⁡ β l m p c o s 2 ⁡ α, B 2 (1,1) = m p s i n ⁡ α t a n ⁡ α + l m p c o s ⁡ α, B 2 1, 2 = 1 - l m p s i n ⁡ α s i n ⁡ β, B 2 2, 1 = m p s i n ⁡ α t a n ⁡ β, B 2 2, 2 = m p c o s ⁡ α s i n ⁡ β t a n ⁡ β + l c o s ⁡ β

3.2.2와 동일한 방법으로 상태오차를 다음과 같이 정의한다.

e 2 = μ d - μ

(34)

여기서, $μ d = α d β d l d T$ 는 기준값을 의미한다. 그리고 적분기를 도입한 슬라이딩 평면을 다음과 같이 둔다.

σ 2 = e ˙ 2 + κ 1 e 2 + κ 2 ∫ 0 t e 2 d τ

(35)

여기서, $κ 1, κ 2 ∈ R 3 × 3 > 0$ 이다. 3.2.2에서 제시한 설계법과 동일한 과정을 따라 제어입력 식 (36)을 설계할 수 있다.

U 2 = U 2, I S M C + U 2, a d a p t i v e

(36)

U 2, I S M C = B 2 * μ C 2 μ, μ ˙ μ ˙ + H 2 μ + … M 2 μ κ 2 e ˙ 2 + κ 2 e 2 + K 2 s g n ⁡ σ 2 U 2, a d a p t i v e = - B 2 * μ Q^2 μ

여기서, $K 2 ∈ R 3 × 3 > 0$ 이다. 그리고 리아프노프 함수 식 (37)을 도입하면 식(27)~(28)과 동일한 과정으로 안정성을 확인할 수 있으며, 업데이트 식 (38)을 도출할 수 있다.

V 2 = 12 σ 2 T σ 2 + 1 2 λ 2 Q ~ 2 T Q ~ 2

(37)

Q^˙ 2 = - λ 2 M 2 μ - 1 σ 2

(38)

3.2.2와 동일한 방법으로 설계한 제어입력 식 (36)을 식 (17)과 식 (18)에 적용하면 새로운 자세 기준신호( $ϕ - c 2, θ - c 2, ψ - c 2$ )와 ( $p - c 2, q - c 2, r - c 2$ )를 도출할 수 있다. 즉, 3.2.3에서 설계한 제어기를 적용한 경우 식 (19)의 기준신호는 다음과 같다.

Θ c = ϕ c θ c ψ c + ϕ - c 2 θ - c 2 ψ - c 2, ω o, c b = p c q c r c + p - c 2 q - c 2 r - c 2

(39)

4. 시뮬레이션

시뮬레이션을 위한 제어대상의 파라미터는 앞서 수행한 연구²⁾에 적용된 것을 사용하였으며, 이것을 Table 2에 정리하였다.

Table 2

Parameter of controlled system

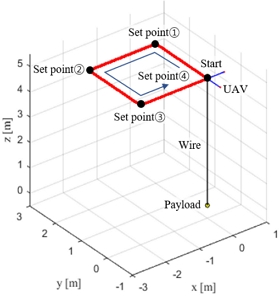
시뮬레이션에서는 본 논문에서 제안하는 세 가지 제어기를 적용하여 화물 거동 안정화 성능을 비교 평가한다. 이를 위하여 길이가 5 m인 와이어와 끝단에 화물을 고정한 UAV를 고려한다. 그리고 Fig. 3에 나타낸 것과 같이 초기위치 (0,0,5)에서 출발하여 각 기준점(0,2,5), (-2,2,5), (-2,-2,5), (0,0,5)으로 순서대로 이동하여 UAV가 비행할 때 발생하는 화물 거동과 이를 억제하는 시뮬레이션을 수행한다. 이는 원거리에서 화물을 배송하는 과정에서 착륙지점 부근에 도착하여 화물 거동 안정화 제어기를 적용한 상황으로 고려해 볼 수 있다. 이에 따라 화물 거동 초기조건을 α=2.5 deg, β=2.5 deg으로 비행으로 인하여 화물이 UAV와 비틀어진 상황을 고려하였다.

Fig. 3

Set point and desired route of UAV

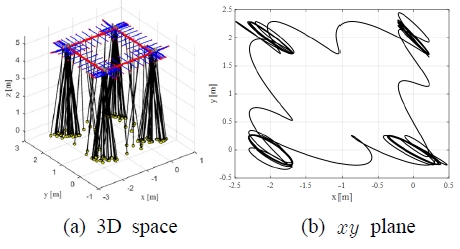
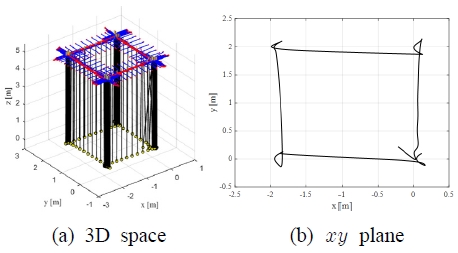
시뮬레이션 결과를 Fig. 5~8에 나타내었다. Fig. 5~7의 (a)는 UAV와 화물의 거동을 2초 간격으로 3차원 공간에 나타내고, (b)는 xy평면에 나타난 화물 거동을 나타낸다. 그리고 시간영역에 대한 화물의 x축과 y축 위치를 Fig. 8에 나타내었다.

여기서 Uncont.는 UAV 위치 및 자세제어기는 적용하였으나 화물 거동 안정화 제어기를 적용하지 않은 경우, compensator는 3.2.1에서 설계한 위치보 상기를 적용한 경우, AISMC는 3.2.2에서 설계한 적응형 적분슬라이딩모드 제어를 적용한 경우, W-AISMC는 3.2.3에서 설계한 능동 윈치기반 적응형 적분슬라이딩모드 제어를 적용한 경우를 나타낸다.

먼저 제어기를 적용하지 않은 경우 Fig. 4 (a)에서 확인할 수 있듯이 UAV가 각 기준점으로 이동하면서 각도 α, β가 변동하였고 이것은 결국 화물이 목표지점으로부터 0.5 m 벗어난 영역 내에서 억제되지 않고 지속적으로 횡운동하는 결과를 나타내었다.

Fig. 4

Suspended position response without payload stabilization control

Fig. 5는 3.2.1에서 설계한 위치 보상기를 적용한 결과로, Fig. 5 (a)는 Fig. 4 (a)와 비교하였을 때 α, β 값이 현저히 감소하였음을 알 수 있다. Fig. 5 (b)는 Fig. 4 (b) 결과 대비 비교적 화물 거동이 안정화된 결과를 나타내었으나, UAV 진행방향으로 발생하는 화물 운동은 효과적으로 억제하지 못하였음을 나타낸다.

Fig. 5

Position compensator control performance

Fig. 6에서는 3.2.2에서 설계한 적응형 적분형슬라이딩모드 제어기가 적용된 시뮬레이션 결과를 나타내고 있다. 기체가 각 기준점에 도착한 후 발생한 화물 횡운동은 위치 보상기를 적용한 경우에 비해 효과적으로 억제되어 목표지점 부근에서 운동하는 것을 확인할 수 있다. 그러나 Fig. 6 (b)와 Fig. 8에서 확인할 수 있듯이 정상상태오차와 잔여 주기운동 특성을 갖는 결과를 나타내었다.

Fig. 6

Adaptive integral sliding mode control performance

Fig. 7

Active winch based adaptive integral sliding mode control performance

Fig. 8

Time response of suspended payload

Fig. 7은 3.2.3에서 설계한 능동 윈치기반 적응형 적분슬라이딩모드 제어기를 적용한 시뮬레이션 결과를 나타낸다. 윈치를 사용하지 않은 경우와 비교하여 정상상태오차와 잔여 주기운동 진폭이 현저히 감소되었으며, 목표지점에 효과적으로 수렴하는 것을 확인할 수 있다. 그러나 시뮬레이션 시간 50 s, 100 s, 150 s에서 각 x, y축 방향에 대한 운동특성이 상호 간 간섭하는 것으로 나타났다. 이것은 제어기 이득 행렬의 3열에 의한 결과로 나타난 것이며 UAV가 빠르게 이동하는 경우 나타나는 현상으로 화물 하역 작업에는 문제되지 않는다.

5. 결 론

본 논문에서는 UAV를 활용한 화물 운송 시 발생하는 화물 거동의 안정화 제어계 설계법에 대하여 고찰하였다. 먼저 화물을 지지하는 와이어 길이를 제어변수로 고려하여 와이어 기반 화물 운송용 UAV시스템 모델링을 수행하였다. 이를 이용하여 세 가지 화물 안정화 제어기를 설계하였다. 첫 번째로 제어기는 좌표기반 위치 보상기를 제안하였다. 두 번째는 적응법칙을 갖는 적분형 슬라이딩모드 제어기를 제안하였다. 여기서 첫 번째 및 두 번째 제안한 제어기는 와이어 길이를 제어변수로써 고려하지 않고 상수로 두었다. 즉, UAV 기체 제어를 통해 화물 안정화를 달성하고자 하였다. 세 번째로 제어기는 와이어 조절용 능동 윈치를 이용한 적응형 적분형 슬라이딩모드 제어기를 제안하였다. 즉, UAV 기체 제어와 와이어 길이를 능동적으로 제어함으로써 화물 거동 안정화 목적을 달성하고자 하였다.

시뮬레이션을 통해 본 논문에서 설계한 제어기의 유효성을 각각 검증하고 성능 비교평가 통해 우수한 제어계 설계법을 도출하였다. 본 논문에서 제안하는 제어계 설계법을 향후 실험을 통해 평가할 예정이다. 특히, 일반적인 FC를 이용하여 본 논문에서 제안하는 제어시스템을 구현하는 경우 과도한 연산량으로 인해 제어성능이 저하될 수 있으며, 기체 안정성을 보장할 수 없다. 따라서 향후 영상처리, 제어시스템 연산 및 FC제어 등 상위 계층 제어시스템 연산 할당을 위해 MC(mission computer)를 도입하여 복합 임무수행용 제어시스템을 구축할 것이다.

Acknowledgments

이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단(No. RS-2022-00166571)의 지원, 교육부의 재원으로 한국산업기술진흥원(KIAT)이 주관하는 ‘부경대학교 대학 내 산학연협력단지 조성사업’의 지원 및 2022학년도 부경대학교의 지원(202203460001)을 받아 수행된 연구임.

Author contributions

D. H. Lee; Conceptualization. D. H. Lee; Data curation. D. H. Lee; Formal analysis. K. J. Cho; Funding acquisition. J. J. Lim; Investigation. J. J. Lim; Methodology. J. J. Lim; Project adminstration. J. J. Lim; Resources. D. H. Lee; Software. D. H. Lee; Supervision. D. H. Lee; Validation. D. H. Lee; Visualization. J. J. Lim; Writing-original draft. D. H. Lee; Writing-review & editing.

References

M. K. Seo and H. J. Kim, 2018, “A Study on Possibility for Commercialization of Logistics Delivery utilizing Drone in Korea”, Korea Internet Electronic Commerce Association, 18(6), 377-393. [https://doi.org/10.37272/JIECR.2018.12.18.6.377]
J. J. Lim, 2022, “A Study on Position Stabilization of Suspended Payload on UAV for Sliding Mode Control Based”, Ph.D thesis, Pukyong National University, Busan, Korea.
J. J. Lim, D. W. Kim, W. H. Hong, M. Kim, D. H. Lee, S. Y. Kim and J. H. Jeong, 2022, “Application of Convolutional Neural Network (CNN) to Recognize Ship Structures”, Sensors, 22(3824). [https://doi.org/10.3390/s22103824]
T. Chen and J. Shan, 2020, “A Novel Cable-Suspended Quadrotor Transportation System: From Theory to Experiment”, Aerospace Science and Technology, 104(105974). [https://doi.org/10.1016/j.ast.2020.105974]
I. Palunko, P. Cruz and R. Fierro, 2012, “Agile Load Transportation : Safe and Efficient Load Manipulation with Aerial Robots”, in IEEE Robotics & Automation Magazine, 19(3), 69-79, Sept. [https://doi.org/10.1109/MRA.2012.2205617]
I. Maza, K. Kondak, M. Bernard and A. llero, 2010, “Multi-UAV Cooperation and Control for Load Transportation and Deployment”, J Intell RobotSyst. [https://doi.org/10.1007/s10846-009-9352-8]
N. Michael, J. Fink and V. Kumar, 2011 “Cooperative manipulation and transportation with aerial robots”, Auton Robot 30, 73-86. [https://doi.org/10.1007/s10514-010-9205-0]
S. Dai, T. Lee and D. S. Bernstein, 2014, “Adaptive control of a quadrotor UAV transporting a cable-suspended load with unknown mass”, 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 6149-6154. [https://doi.org/10.1109/CDC.2014.7040352]
Y. Fan, H. Guo, X. Han and X. Chen, 2022, “Research and Verification of Trajectory Tracking Control of a Quadrotor Carrying a Load”, Applied Sciences, 12(3(1036)). [https://doi.org/10.3390/app12031036]
M. E. Guerrero-Sánchez, R. Lozano, P. Castillo, O. Hernández-González, C. D. García-Beltrán and G. Valencia-Palomo, 2021, “Nonlinear Control Strategies for a UAV Carrying a Load with Swing Attenuation”, Applied Mathematical Modelling, 91, 709-722. [https://doi.org/10.1016/j.apm.2020.09.027]
T. Kusznir and J. Smoczek, 2020, “Sliding Mode-Based Control of a UAV Quadrotor for Suppressing the Cable-Suspended Payload Vibration”, Journal of Control Science and Engineering, 2020, Article ID 5058039. [https://doi.org/10.1155/2020/5058039]
B. Barikbin and A. Fakharian, 2019, “Trajectory Tracking for Quadrotor UAV Transporting Cable-Suspended Payload in Wind Presence”, Transactions of the Institute of Measurement and Control, 41(5), 1243-1255. [https://doi.org/10.1177/0142331218774606]
S. Yang and B. Xian, 2018, “Robust Control Design for the Quadrotor UAV with a Suspended Payload”, In Proceedings of the 2018 IEEE 8th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems, 469-473. [https://doi.org/10.1109/CYBER.2018.8688168]
Y. Yang, D. Zhang, H. Xi and G. Zhang, 2022, “Anti‐swing Control and Trajectory Planning of Quadrotor Suspended Payload System with Variable Length Cable”, Asian Journal of Control, 24(5), 2424-2436. [https://doi.org/10.1002/asjc.2679]
X. Li, Z. Mei, D. Zhu and B. Xie, 2017, “Modeling and anti-sway control of ship-mounted crane”, Advances in Mechanical Engineering, 9(9), 1-9. [https://doi.org/10.1177/1687814017727252]
P. Castillo, R. Lozano and A. Dzul, 2005, “Stabilization of a Mini Rotorcraft with Four Rotors”, IEEE Control Systems, 25(6), 45-55. [https://doi.org/10.1109/MCS.2005.1550152]
Mellinger D, Michael N, Kumar V, 2012, “Trajectory generation and control for precise aggressive maneuvers with quadrotors”, The International Journal of Robotics Research. [https://doi.org/10.1177/0278364911434236]

Item	Value	Unit
Type of UAV	Quadcopter	-
Mass of UAV(m_q)	25	kg
Size of UAV [L×W×H]	1×1×0.5	m
Moment of inertia(I_q)	diag(0.0025, 0.0025, 0.0037)	kg·m²
Mass of payload(m_p)	5	kg