긴급후진 시 추진 축계에 발생하는 비틀림 응력과 피로 수명 분석

1.1 연구 배경 및 목적

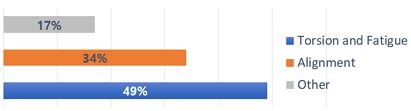
선박의 추진 축계가 받는 진동의 종류는 크게 기관 본체 진동과 축계의 비틀림 진동, 종진동, 횡진동으로 나뉜다. 1900년 독일인 Bauer가 19세기 말부터 20세기 초에 걸쳐 발생한 이유를 알 수 없는 축계 절손 사고의 주된 원인이 비틀림 진동일 것이라는 가정을 처음 제시한 후 2년에 걸쳐 Gumbel과 Frahm이 이를 증명하였다.¹⁾ 그 후 축계 비틀림 진동에 관한 연구 중요성이 커지게 되고 진동을 제어하여 축계 안정성을 도모할 수 있는 방법이 고안되었지만, 그럼에도 불구하고 2002년 국제내연기관연합회(CIMAC) 작업반(WG) 14에서 미국선급협회가 발표한 축계사고 통계자료²⁾를 보면 최근까지도 Fig. 1과 같이 사고 원인의 49%가 재료의 비틀림과 피로파손에 의한 것이라고 보고되었다.

Fig. 1

Shafting, bearing, coupling bolts damage and failure statistics

선박에서 허용 범위를 벗어나 상당한 크기의 비틀림 응력이 발생 가능한 운전모드는 주기관에서 발생하는 가진력의 주기와 고유진동수가 일치하여 공진이 발생하는 운전금지구역(Barred Speed Range)를 통과하거나³⁾ 정상 운전 중에 긴급정지(Crash stopping), 긴급후진(Crash astern)과 같이 추진 축계의 회전 방향을 반대로 하는 후진 운전을 해야 할 때로 꼽을 수 있다. 그중 여러 논문^4-6)에서 선박이 후진 운전을 해야 할 때 상당한 크기의 비틀림 응력이 발생한다고 지적하였음에도 불구하고 후진 운전 시 발생하는 비틀림 응력 변화를 구체적으로 파악하고 해당 운전모드가 추진축의 피로와 피로 수명 단축에 미치는 영향에 관한 연구는 부족한 실정이다.

현재까지 긴급후진 운항 모드에 관한 연구 동향은 대부분 운항모드를 시뮬레이션으로 구현하거나⁷⁾, 긴급정지 시 선로 거리를 줄이기 위한 엔진 최적 운전 방법⁸⁾에 관한 연구들이었다.

따라서 본 논문에서는 중형 유조선을 대상으로 만재흘수 상태에서 긴급후진에 준하는 공시 운전(Official Sea-trial) 절차를 따른 후진 운항모드를 실시하여 이때 발생하는 비틀림 응력 데이터를 계측하여 비틀림 응력 변화를 파악하고 피로-응력 선도(S-N Curve)를 근거로 긴급후진 운전이 축의 피로 수명에 미치는 영향을 연구하고자 한다.

2.1 대상선박과 측정장비의 구성

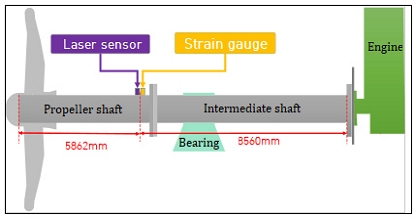
Table 1은 대상선박의 추진계 사양이며 Fig. 2는 비틀림 응력 측정을 위해 시험선에 설치된 레이저 센서와 스트레인 게이지의 위치를 나타낸다. 레이저 센서로 축계의 분당 회전수를 측정했으며, 휘스톤 브리지(Wheatstone bridge) 회로의 스트레인 게이지를 활용하여 축계에 작용한 토크 값을 추적할 수 있도록 했다.

Table 1

Specification of the test ship

Fig. 2

Installation position of sensors

스트레인 게이지는 Fig. 3에서 보는 바와 같이 4개의 저항 R1, R2, R3, R4와 입력전압 V, 출력 전압 E로 구성되어 있다. 게이지는 토크에 의한 축의 비틀림과 같이 미소한 물리적 변화량을 계측하는데 용이하게 사용된다.⁹⁾ 그 원리는 축의 변형률과 저항의 변화량 인자 비율이 반영된 게이지의 게이지 팩터(Gauge factor)를 활용하는 것이다. 식 (1)과 같이 저항의 변형에 비례하는 회로의 출력 전압량을 구하고 본 전압량을 식 (2)에 대입하면 식 (3)을 통해 축계에 작용한 토크 값을 계산할 수 있다.

Fig. 3

Strain gauge and Wheatstone bridge

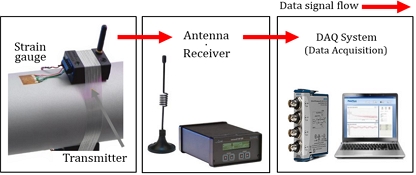
계측된 값을 컴퓨터로 전달하기 위해 Fig. 4와 같이 텔레메트리 시스템을 구성하여 데이터를 수집하였다.

Fig. 4

Telemetry system configuration

2.2 시험 절차

긴급후진 운항 시험절차는 조선소에서 선박 건조 후 선주에게 인도되기 전 수행하는 공시 운전(official sea-trial) 절차를 따랐다. 대상 선박이 상용출력(Normal Continuous Rating, 이하 NCR) 부하로 운전 중일 때 엔진에 정지신호를 주어 엔진 부하를 낮추고, 축의 회전속도가 15 rpm으로 떨어졌을 때 후진 신호를 주어 추진 축계의 역회전을 시작하였다. 후진 운전 시작 후 역방향 회전수를 약 65 rpm까지 상승시키고 6분 정도 후진 운전을 유지한 후 시험을 종료하였다.

공시운전 절차에 따라 수행한 긴급후진 운항은 축계의 추력 방향과 선박의 운동방향에 따라 크게 네 가지 상태로 구분된다.

첫번째는 선박의 윈드밀(Windmill) 상태로 엔진 출력이 NCR일 때 정지신호를 주어 추진계에 동력 공급이 중단되었지만 관성에 의하여 선박은 전진하는 상태이다. 두 번째는 축계 추력방향은 후진방향인 반면, 선체 운동은 전진을 하고 있는 상태로 축계 회전속도가 15 rpm으로 감소할 때 엔진에 후진운전신호를 주어 축계는 역회전을 시작하지만 선박은 관성에 의해 계속 전진한다. 그 다음 축계의 후진추력방향과 전진방향의 힘이 같아지는 스탠드 스틸(Stand still) 상태가 나타나며, 운항속도는 0 knot에 가깝고 전체 공시 운전 과정에서 짧은 시간 관찰된다. 마지막으로 축계 추력방향과 선체 운동방향이 후진 운항에 맞게 각각 역회전 및 후진 운전하게 된다.

2.3 축의 피로 수명 계산방법

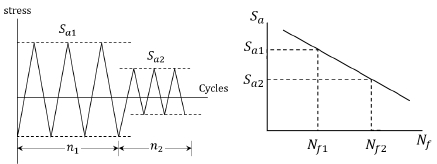
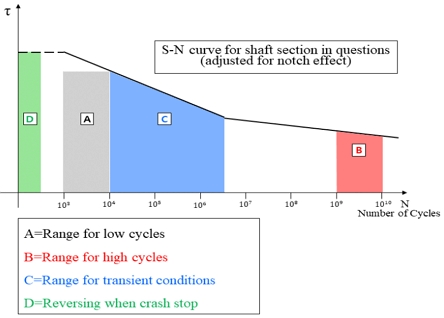
재료가 항복강도보다 작은 응력을 반복적으로 받는 것을 피로(Fatigue)라고 하며, 피로파괴(Fatigue failure)는 피로로 인한 재료 파단을 뜻한다.¹⁰⁾ 이때 피로파괴가 발생하기까지 적용된 반복하중의 횟수를 피로수명(Cycles to failure)이라 하며, 피로수명과 교번응력(S_a)관계를 log-log scale로 표현한 것을 S-N선도라 한다. 현실에서는 재료에 일정한 진폭의 교번응력보다는 운전모드와 환경에 따라 다양한 크기의 응력인 가변응력(Variable stress)에 의한 피로누적이 발생한다. 가변응력에 의한 피로수명을 계산하기 위해 Fig. 5의 S-N선도와 식 (4)의 Palmgren-Miner식을 활용할 수 있다.¹¹⁾ 임의의 크기의 교번 응력이 재료에 작용하여 실제 누적된 사이클 수를 n_i이라고 정의하며, N_fi는 피로 파손이 일어나는 사이클 수, 즉 피로 수명을 뜻한다. 해당 식에서 하나의 항은 임의의 교번응력에 의한 부분손상(Fractional damage)이다.

Fig. 5

Different amplitude stress blocks and S-N curve

상기 내용을 바탕으로 선박의 추진축을 반복 하중을 받는 재료라고 간주하여 추진축의 피로 수명에 관해 정의된 규정은 DNV-CG-0038 Calculation of shafts in marine application¹²⁾이 유일하며, 독일의 샤프트 부하 용량 계산 기준서인 Calculation of load capacity of shafts and axles DIN 743을 바탕으로 한다. 해당 DNV 기준서는 시간영역에서 피로 누적을 계산할 수 있게 하였다.¹³⁾

Fig. 6은 기준서에서 제시하는 반복응력의 피로 수명에 관한 것으로, 이는 선박의 운항모드에 따라 추진축에 발생하는 다양한 범위의 비틀림 응력을 거시적으로 표현한 것이며, 축이라는 재료의 일반적인 피로-수명 선도라고 이해할 수 있다. 추진축의 피로-수명 선도는 축계 사양에 따라 다르며 시험선의 고유한 선도를 그리기 위해 DNV-CG-0038에서 제시하는 피로 기준(Fatigue criteria)를 따랐다.

Fig. 6

Applicable load cycles for marine propulsion system

상기 내용을 종합하여 본 연구에서 도출하고자 하는 축의 피로 수명을 계산하는 전체 과정은 Fig. 7과 같으며, 각 단계별 자세한 내용은 다음과 같다.

Fig. 7

Flow of fractional damage calculation

2.3.1 피로 기준 계산방법

첫 번째는 앞서 설명하였듯이 시험선의 고유한 피로-수명 선형 그래프를 그리기 위한 두 가지 기준점 저 사이클 (Low-cycle fatigue, 이하 LCF), 고 사이클 (High-cycle fatigue, 이하 HCF)을 찾는 피로 기준 계산이다. 계산과정에서 Table 2의 시험선 축계요목이 반영되었으며, LCF는 피로-수명 선도에서 10⁴의 반복하중 횟수에 축이 파단되는 지점을 뜻하며 HCF는 3×10⁶번의 반복하중이 작용하면 축이 파단되는 지점을 의미한다.

Table 2

Table of shaft specification

LCF(τ_vLC), HCF(τ_vHC) 기준의 자세한 정의와 복잡한 계산 과정은 DNV-CG-0038에서 확인할 수 있으며, 본 논문에서는 축계 사양에 맞게 도출된 최종 기준 계산식 (5), (6)을 적용하였다.

$\[ {\tau }_{vLC}=\frac{{\sigma }_y}{2S_L{K}_L}-\tau \]$

(5)

$\[ \begin{array}{c}{\tau }_{vHC}=\frac{0.24\cdot {\sigma }_y+42-0.15\cdot \tau }{K_H\cdot S_H}\hfill \\ \left(\tau ={\tau }_0\times {\lambda }^2\right)\hfill \end{array} \]$

(6)

• S, 안전계수　　　 σ_y, 항복강도
• J, 영향계수　　　 λ, 속도비
• τ₀, MCR에서의 공칭응력
• τ, rpm에 따른 공칭응력

이에 따라 시험 선박의 중간축의 LCF, HCF 기준값은 Table 3과 같다.

Table 3

LCF, HCF Criteria according to rpm

여기서 주목할 점은 rpm에 따라서 두 기준값이 변한다는 점이다. 이것은 피로 수명 해석을 위해 피로-수명 선도를 그리기 위한 두 기준점 τ_vLC, τ_vHC 이 rpm에 따라 다르며, 중간축의 고유한 피로-수명 선도가 축의 분당 회전수에 따라 각기 다르다는 것을 뜻한다.

2.3.3 부분 손상 계산

계측된 데이터에서 평균응력을 기준으로 시간에 따른 교번응력 τ_v (S_a)를 산출한 뒤 각 교번응력을 해당 rpm의 피로-수명 선도에 적용하여 부분 손상을 계산하였다. 시험 초반에 계측된 응력의 계산 결과 예시는 다음 Table 4와 같다.

Table 4

Partial examples of fractional damage

3.1 계측된 비틀림 응력 분석

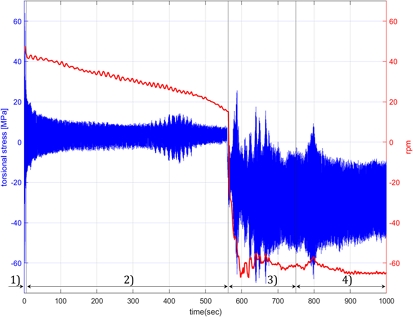
본 연구에서 수행한 긴급후진 운전모드에서 계측된 비틀림 응력을 분석한 결과는 Fig. 8과 같다.

Fig. 8

Measured torsional stress and rpm

1)에서 엔진의 연료 공급이 차단되면 2)와 같이 축계의 분당 회전수는 서서히 줄어들기 시작한다. 15 rpm으로 엔진 부하가 떨어진 시점에 후진 운항모드를 시행하였다. 회전수가 증가함에 따라 추진 축계는 과도 상태가 되어 비틀림 응력이 급격히 증가하는 것을 3)에서 확인할 수 있다. 과도 상태를 지나 역방향 회전수가 65 rpm, NCR의 78%에 도달하여 운전이 어느 정도 진행되면 4)와 같이 응력이 상대적으로 줄어드는 것을 확인하였다. 1)~4)의 경계는 선박의 엔진 사양과 선박의 크기 및 흘수 상태에 따라 달라진다.¹⁴⁾

3.2 평균응력 변화

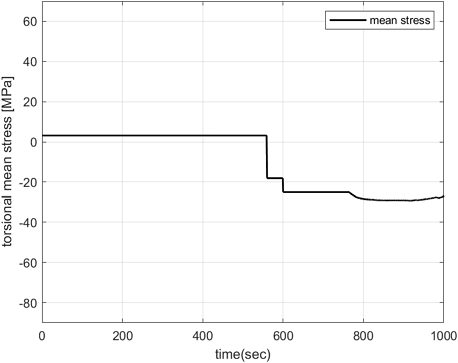
아래 Fig. 9는 시간에 따른 비틀림 평균응력변화를 나타낸 것이다. 그림에서 보는 바와 같이 평균응력은 후진 운항모드가 시행되기 전까지 거의 ‘0’에 가깝다가 축계의 역방향 회전이 시작되면서 평균 응력의 절댓값이 증가하는 것을 확인할 수 있다. 평균 응력의 변화는 피로 수명에 영향을 미치는데 이를 평균응력 효과라고 한다. 평균응력 효과란 응력진폭이 같더라도 평균 응력이 ‘0'이 되는 양진에서 평균응력이 ‘0’을 벗어나는 편진 인장 반복응력이 하중으로 작용하면 재료의 피로수명은 줄어들고 피로한계응력 또한 감소하게 된다. 이를 통해 후진 운항모드가 축의 피로 수명 단축에 영향을 미치는 것을 확인할 수 있었다.

Fig. 9

Torsional stress and mean stress

3.3 주요 부분 손상

Table 5에서 보는 바와 같이 시험 시작 후 587초에 역회전으로 인한 최대 비틀림 응력이 확인되었다. 이에 따라 긴급후진 운항모드 시작 시 추진축에 가장 큰 부분손상이 발생하였음을 알 수 있었다.

Table 5

Major fractional damage

3.4 긴급후진 운항모드에 따른 피로수명

계측 데이터를 분석하여 계산된 부분손상의 총계, 다시 말해 해당 시험선이 만재흘수(Full laden)상태에서 긴급후진 운항모드를 1회 실시할 때 축에 누적된 손상은 5.15×10^-06이었다. 해당 값이 1에 도달하면 축은 피로 파괴되는 것으로 이해할 수 있는데, 피로 누적 1을 축의 수명을 30년으로 대입하여 가정한다면 본 시험을 통해 누적된 손상 5.15×10^-06은 1.35시간에 해당하였다. 시험 선박 축의 생애를 30년으로 가정하면 본 실험과 동일한 방법 및 과정으로 긴급후진 1회 운전 시 축의 수명이 1.35시간 단축되며, 2회 운전 시 2.7시간, n회 운전 시 1.35n시간 단축되는 것을 유추할 수 있었다.

Author contributions

H. J. Choi; Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Resources, Writing-original draft. K. H. Seo; Investigation, Writing-review & editing. Y. M. Kim; Investigation, Visualization. J. W. Lee; Supervision, Validation, Writing-review & editing. J. U. Lee; Funding acquisition, Project adminstration, Supervision, Validation, Writing-review & editing.