어로시스템 안전성 및 안전제어 기준의 추정을 위한 권양력 연구
초록
본 논문에서는 통발 양승기 어로시스템의 구조와 성능을 심도 있게 분석하고, 안전성과 안전제어 기준을 확립하기 위해 유압 시스템 최적화를 목표로 한다. 양승기는 롤러와 드럼으로 구성된 기계 장치이며, 이를 구동하는 유압장치로 작동한다. 논문에서는 시스템 설계 시 외부 및 내부 변수에 대응할 수 있는 정량적 수학적 모델을 수립하였고, 본드선도를 사용해 장치의 수치 모델식을 완성하였다. 시뮬레이션을 통해 외부 부하력 변화에 맞는 권양력 제공을 위한 장치 사양을 제안함으로써, 유압 시스템 설계, 성능 개선, 안전제어 기준 추정을 위한 중요한 기초 자료를 제공하고자 한다.
Abstract
This paper aims to deeply analyze the structure and performance of the pot-hauler fishing system and optimize the hydraulic system to establish safety and safety control standards. The pot-hauler consists of a mechanical device composed of rollers and drums, which operates through a hydraulic device generating hydraulic power. The study establishes a quantitative mathematical model to address both external and internal variables in system design and completes the numerical model equations of the device using bond graphs. Through simulations, the specifications of the device required to provide hoisting force in response to changes in external load are proposed. This research provides essential foundational data for hydraulic system design, performance improvement, and the estimation of safety control standards.
Keywords:
Fishing System, Pot Hauler, Hauling Force, Hydraulic Systems, Numerical Analysis키워드:
어로시스템, 양승기, 권양력, 유압시스템, 수치 해석1. 서 론
현재 한국의 연·근해 어업은 수산자원 고갈과 어장 오염으로 어획량이 감소하면서 기본적인 안전조업이 이루어지지 않고 있으며, 인력 감소와 고령화로 인해 과도한 어로활동과 해양사고가 증가하고 있다.
해양사고에서 어선이 차지하는 비율은 매우 높아 2023년 해양사고는 총 3,092건으로 2022년 대비 229건(8.0%) 증가했으며, 그 중 어선사고가 2,047건(66.2%)을 차지하고 있고, 2022년 대비 329건(19.2%)이 증가하였다.
그 중 주요사고 672건의 내용을 살펴보면, 충돌 265건(39.4%), 안전사고 140건(20.8%), 화재·폭발 140건(20.8%), 전복 71건(10.6%), 침몰 56건(8.3%) 순으로 발생하였으며, 단순 사고(2,420건) 중에는 기관손상이 917건(37.9%)으로 가장 많았다. 2022년과 비교했을 때 2023년의 주요사고 발생 건수는 비슷(1건 감소)하였으나, 단순사고는 전년 대비 230건(10.5%)이 증가한 것으로 나타났다. 2023년 해양사고로 인한 사망·실종자는 총 94명으로, 이중 안전사고로 인한 인명피해는 55명(58.5%)이다. 그 밖에 전복사고 16명, 충돌사고 13명, 침몰사고 4명, 기타사고(행방불명 5, 접촉 1)로 6명의 인명피해가 발생하였다. 어선 해양사고의 경우, 주요한 원인이 복잡한 유형이 아니라 원인 및 대책 모두가 명백한 내용으로 반복적으로 발생하고 있고, 어선 해양사고 원인 중 60% 이상이 인적과실로서 해양사고의 합리적인 대응책 마련이 시급하다.
어선어업은 다양한 기계장비와 어구를 사용하여 사고 위험이 높은 업종이지만, 현재 어로시스템에 대한 체계적인 관리가 부족해 안전기준 마련이 시급하다. 특히 어로시스템의 자동화가 진행되면서 설비 운용의 위험성도 증가하고 있으며, 이에 대한 기초 연구와 기술 교육이 부족하여 예기치 못한 사고가 빈번하게 발생하고 있다.
기존 양승기는 제작자의 경험에 의존하여 장비 사양이 결정되었기 때문에,1,2) 작업 환경 변화에 신속하게 대응하기 어려웠고, 그로 인해 제작 비용이 증가하는 문제가 발생하였다. 이에 본 연구에서는 양승기의 권양 무게 변화와 속도를 동적 변수로 설정하고, 외부 부하력 변화에 따른 구동 동력 변화를 반영한 수학적 모델을 개발하였다.
본 연구의 목표는 어로시스템의 기계 및 유압 장치에 대해 부하력 모델링과 수치해석을 통해 시뮬레이션을 수행하고, 양승 과정에서 발생하는 부하 변동과 권양력을 실시간으로 추정하여 안전제어 기준을 정량적으로 제안하는 것이다. 이를 위해 통발 양승기의 기계 및 유압 장치를 대상으로 외부 및 내부 변수들을 고려한 수학적 모델식을 도출하여 시스템의 사양을 정량적으로 계산하였다.
또한 본드선도(Bond Graph) 모델링 기법을 사용하여 에너지 보존 법칙에 기반한 장치 간 상호작용을 분석하였고, 이를 통해 양승기 구동 시스템의 동적 모델식을 도출하였다. 이 모델링 기법을 통해 양승기 시스템의 정확한 사양을 결정할 수 있으며, 외부 환경 변화에 신속하게 대응할 수 있는 기초 자료로서 활용될 수 있을 것으로 기대한다.
2. 재료 및 방법
2.1 양승기 구동장치의 최적화
이 연구에서는 양승기를 구동시키는 유압 시스템에 사용되고 있는 장치들의 사양들을 정량적으로 구할 수 있도록 외부 영향 및 내부 영향에 대한 변수들을 선정하여 모델식을 유도하였다.
양승기에 사용되는 구동 시스템의 사양을 정량적으로 계산하기 위하여 양승기의 권양 무게 변화, 롤러 및 드럼과 줄과의 마찰력의 변화, 외부 압착력을 동적 변수로 두고 양승 속도를 구하는 모델식을 유도하였다. 따라서 양승기 기계 장치의 주요 제원(롤러 등)도 고려하여 정적 상태의 변화도 같이 고려하여 모델식을 유도하였으므로 양승기 구동장치의 사양 결정 및 권양력을 결정하는 데 있어 구체적인 적용 범위와 정확도가 향상될 것으로 판단하였다.
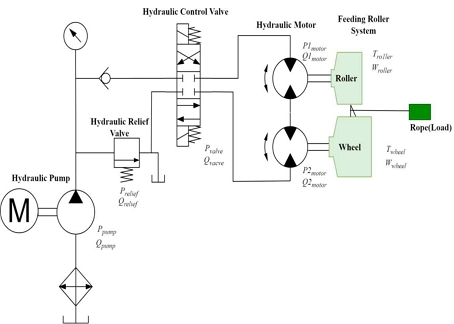
이 연구에서 대상으로 한 양승기 장치의 구성도를 Fig. 1에 나타내었다.
2.2 어로시스템 동적모델링
양승기에 사용되는 유압 장치의 동력은 외부 환경에 해당하는 양승 무게와 양승 속도 및 내부 환경에 해당하는 롤러와 드럼의 사양 등 기계 요소들에 따라서 달라지므로 아래의 조건을 가정하고 모델링을 수행하였다.
- • 유압 장치에 공급되는 유압 압력을 조정하는 릴리프 밸브의 동적 특성은 고려하지 않는다.
- • 유압 펌프의 회전수는 외부 부하량에 관계없이 일정하다.
- • 유압 장치의 누설은 없다고 간주한다.
- • 유압 관로 내 유압 작동유의 흐름은 층류이며, 관로 내 마찰은 무시한다.
- • 유압 밸브의 반응 시간은 20 Hz로 간주한다.
- • 유압 라인 내경은 2.54 mm를 선정하였다.
- • 줄의 질량, 탄성, 탄성력은 무시한다.
- • 드럼과 롤러의 질량과 관성력은 무시한다.
- • 양승기 드럼과 줄 사이의 마찰은 1~7.5 N 사이의 값을 입력하여 계산하였다.
- • 롤러와 롤러 사이의 정마찰력 계수는 2 Nms/rad, 쿨롱 마찰 계수는 1 Nms/rad으로 두고 계산하였다.
- • 베어링 등 기계 요소에서 발생하는 마찰력은 무시한다.
- • 양승기 권양 시 롤러와 줄 사이에는 슬립(slip)이 없다고 간주한다.
- • 권양 시 끌어올리는 무게는 줄에 걸리는 그물의 무게와 그물 내 어획물의 무게를 합한 값이다.
이와 같은 조건들을 바탕으로 모델링과 시뮬레이션을 수행하여 유압장치와 권양 시스템의 동작을 분석하였다.
이 연구에서 사용된 모델링 기법은 본드선도(Bond graph)기법3-5)을 이용하여 구하였다. 본드선도 모델링은 에너지 보존의 법칙에 근간을 두고 각 장치간의 상호 작용을 약속한 기호로 표현하여 모델식을 구한다. 어떤 장치에서 변화하는 모든 물리량은 그 장치에 대한 에너지 특성에 따라 작력 요소(e, effoet sourse)와 흐름 요소(f, flow source)로 표현할 수 있으며, 본드선도의 구성 요소인 기본 요소, 일률 흐름, 인과 관계 및 접합 관계를 고려하여 적절하게 결정함으로써 전체 장치에 대한 상호 에너지 관계를 파악할 수 있다.
동적 시스템을 본드선도로 모델링할 때 필요한 기본적인 요소들은 참고문헌6-9)을 참고하였다.
통발 양승기가 포함된 기계장치와 유압장치의 기본 구성도를 Fig. 2에 나타내었다.
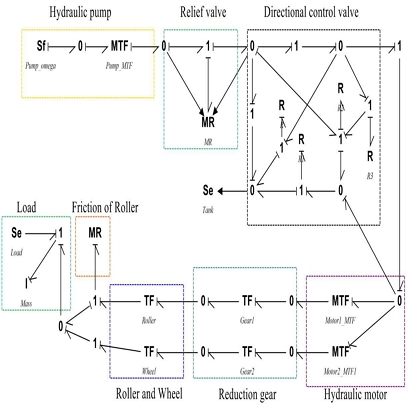
각각의 유압 장치와 기계 장치의 모델링은 본드선도를 이용하여 동적 모델식을 유도하였으며, 유도된 본드선도를 Fig. 3에 나타내었다.
1) 유압 펌프
유압 펌프는 정용량형으로 운전 회전수는 1,800 rpm, 펌프의 배제 용량은 3.88889×10-5 m3/rev이다. MTF(modulated transformer)를 이용하여 기계 요소를 유압 요소로 바꾸었으며, 변환식은 아래와 같다. 변환 계수는 펌프의 배제 용량을 사용하였다.
Ppump, Qpump는 유압 펌프에서 발생되는 압력(Pa) 과 유량(m3/s)을 의미하여, Telectric motor, ωelectric motor는 전동기의 토크(Nm)와 각속도(rad/s)이다.
| (1) |
| (2) |
2) 릴리프 밸브
유압 시스템의 최대 압력은 1.40×107 Pa(142.7603 kgf/㎠) 로 설정하였다.
Pre-valve, Qre-valve는 릴리프 밸브에서 발생되는 압력과 유량이다. MR은 유압 펌프와 방향제어 밸브로 들어가는 유량의 차로 표시하였다.
| (3) |
| (4) |
3) 방향제어 솔레노이드 밸브
솔레노이드 4-port & 3-position형 방향제어 밸브를 사용하였으며 중립 위치에서 스풀 위치는 closed type이며, 밸브 반응 시간은 20 Hz이고, 유량 계수는(discharge coefficient) 0.6으로 설정하였다. 스풀(spool)과 스풀시트(spool seat) 사이의 간극은 없다고 간주하였다. 유압 모터 출구에서 나오는 유량은 밸브를 경유하여 유압 탱크로 들어간다.
| (5) |
| (6) |
여기서, Pdi-valve, Qdi-valve는 방향 제어 밸브에서 발생되는 압력과 유량이며, 밸브 내 포트(port)에서 발생되는 저항은 식 (6)으로 표시하였다. Pdiin-valve, Pdiout-valve는 밸브에 들어가는 입력과 출구의 압력을 의미하여, Cd는 유량계수, A는 밸브 내 포트 단면적(m2), ρ는 유압 작동유의 밀도(kg/m3)이다.
4) 관로
관로에서 유압 작동유의 모델은 마찰과 관성력을 고려하여 모델링하였다. 유압 작동유의 밀도는 860 kg/m3을 사용하였다. 관로 내 유압 작동유의 동특성은 고려하지 않았다. 만약 양승기의 관로의 단면적이 작거나 길이가 상당히 길면 관로 내 유압 작동유의 동특성(관로 내 저항 및 유압 작동유의 관성 고려)도 고려해서 관로 모델식에 반영해야 한다.
5) 유압모터
유압 모터는 양방향 회전형으로 배제 용량은 3.1×10-4 ㎥/rev이며, 기기 내 회전 마찰과 기계 부품의 회전 관성은 고려하지 않았다.
Phy-motor, Qhy-motor는 유압 펌프에서 발생되는 압력과 유량을 의미하여, MTF는 모터의 배제 용량을 고려한 변환식을 이용하였다.
| (7) |
| (8) |
6) 드럼(Wheel)
드럼의 직경은 0.45 m이며, 드럼과 그물과의 마찰 계수는 임의의 값을 선정하였는데 드럼에 고무가 삽입된 구조물이므로 고무의 마찰 계수를 고려하여 선정하였다. 시뮬레이션 결과는 마찰 계수를 0.4, 0.6, 0.8, 2로 선정하여 특성을 파악하였다. 드럼에서 발생하는 동력은 본드의 변환 요소를 이용하여 아래와 같이 나타낼 수 있다.
| (9) |
| (10) |
여기서, Fdrum-1,2,3, Qdrum-1,2,3는 각각의 드럼에서 발생되는 힘(N)와 속도(m/s)를 나타낸다. MTF은 드럼의 반경(m)이다.
7) 부하력(Load Force)
그물과 그물 내 내용물을 합하여 부하력으로 계산하였으며, 외부 부하력은 7,840 N을 기준으로 하여 양승기에서 발생되는 권양력의 변화를 수치 해석하여 시뮬레이션하였다.
| (11) |
| (12) |
여기서, Fload, vload는 그물을 끌어올리는데 필요한 힘과 이때 발생되는 속도를 의미한다. Cload, Iload는 힘과 속도를 구하기 위한 변환 계수로 각각 중력 방향의 부하력과 그물의 질량을 대입하였다.
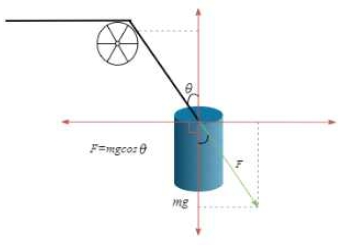
8) 도르래(Pulley)
부하력이 걸려 있는 줄은 도르래를 거쳐서 양승기의 드럼으로 전달되는데, 이때 도르래의 영향으로 인하여 부하력은 감소 현상이 발생한다. Fig. 4는 도르래에 걸리는 힘의 영향을 도식화하여 나타낸 것이다. 부하질량 m, 중력가속도 g, 도르래와 부하 사이의 각도(degree) θ라 하면 도르래에 의하여 줄에 걸리는 힘은
| (13) |
이다. 시뮬레이션을 수행하면서 각도는 30°를 기준으로 하여 각도는 변화를 시켜가면서 수치해석을 수행하였다.
9) 마찰력(Friction Force)
롤러와 줄 사이에는 고체 마찰이 작용한다. 표면에서 마찰력의 방향은 서로 미끄러지는 상대 운동의 반대 방향이 된다. 고체 마찰에서 주요한 점은 한 물체가 다른 물체에 대해 상대 운동을 하거나 상대 운동을 시작하려 하는 순간이다. 마찰력은 운동의 발생은 막는데 필요한 값(정 마찰의 극한 값)보다 절대 클 수가 없다. 정적으로 평형 상태에 대해 두 표면이 서로 상대적으로 정지해 있는 상태에 대해 접촉력의 법선 성분과 접선 성분 사이의 관계를 고려해야 한다.
마찰력에 관하여 해석하기 위해서는 우선 운동이 발생하지 않는 것으로 가정할 때, 접촉 면적에 운동이 발생할 때, 접촉 면적에서 운동이 발생하지만 운동의 형태 등을 고려한 마찰 모델이 필요하다.
LuGre 마찰 모델은 마찰력 모델 중 하나로서, 마찰력이 일어나는 두 표면의 접촉면을 정지 마찰력, 동적 마찰력과 클롱 마찰력으로 표현할 수 있어서 비교적 현실적으로 사용되는 모델이다.6)
이 연구에서는 정지 마찰 계수는 2, 클롱 마찰계수는 1, 점성 마찰 계수는 0.01, 스트리벡 변환 속도는 0.001 m/s 선정하고 외부에서 마찰력의 크기를 가변하여 시뮬레이션을 수행하였다. 가변 정수는 임의의 값을 대입하였다.
10) 드럼과 줄 사이의 마찰력10)
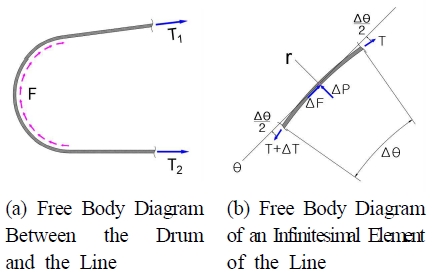
기계에서 기계의 한부분에서 다른 부분으로 에너지를 전달할 때 벨트 구동 방식을 이용한다. 마찰이 없으면 벨트는 드럼에서 미끄러지게 되고 동력 전달은 불가능하게 된다. 양승기에 사용되고 있는 줄은 드럼과 접촉을 통하여 힘을 전달하는데, Fig. 5는 드럼에 걸쳐 있는 줄과 자유물체도와 줄의 미소 요소에 대한 자유물체도를 나타낸 것이다.
줄의 미소 요소에는 마찰력 ΔF와 수직력 ΔP가 포함되어 있다. 줄의 장력 T1과 T2는 미소 요소 한쪽에서 T이고 점점 증가하여 다른 한쪽에서 T+ΔT가 된다. 반경 방향으로 평형식을 적용하면 다음 식 (14)와 같다.
| (14) |
원주 방향으로 힘의 평형식을 적용하면 다음 식 (15)와 같다.
| (15) |
위 식을 ΔF로 정리하면 다음 식 (16)으로 정리된다.
| (16) |
Δθ→0으로 보내는 극한을 취하면 줄은 미소 요소에서 작용하는 수직력 ΔP는 영(zero)이 됨을 식 (14)에서 확인할 수가 있다. 그리고 수직력이 영이 될 때 줄에 작용하는 마찰력도 영이 되어야 한다. 따라서 줄의 미소요소에서 장력의 변화량도 영이 되어야 함을 식 (16)으로부터 확인할 수가 있다.
최종적으로 마찰 모델의 관계식을 전개하여 식 (17)을 얻을 수 있었다.
| (17) |
여기서, T1과 T2는 줄의 장력, μs는 마찰계수, β = θ2 - θ1는 줄과 드럼이 접촉하는 부위에 대한 드럼의 중심각도를 의미한다.
마찰계수 (μs)enh는 식 (18)을 통해 얻을 수 있다.
| (18) |
이 연구에서는 유도된 식 (17)를 이용하여 줄과 드럼 사이의 힘의 전달을 모델식에 적용하였고 각도는 315°로 선정하였다.
3. 결과 및 고찰
3.1 수치해석에 사용된 파라미터 및 프로그램
수치해석 시뮬레이션 프로그램에 사용된 주요 파라미터, 값, 및 단위는 Table 1과 같다. 단위는 SI단위를 사용하여 주요 수치해석 결과 값을 계산하였다. 본드선도를 이용하여 모델링을 수행한 후, 시뮬레이션 프로그램은 20-sim11)을 이용하였으며, 수치적분은 Backward Differentiation Formula (BDF)를 이용하여 계산하였다.
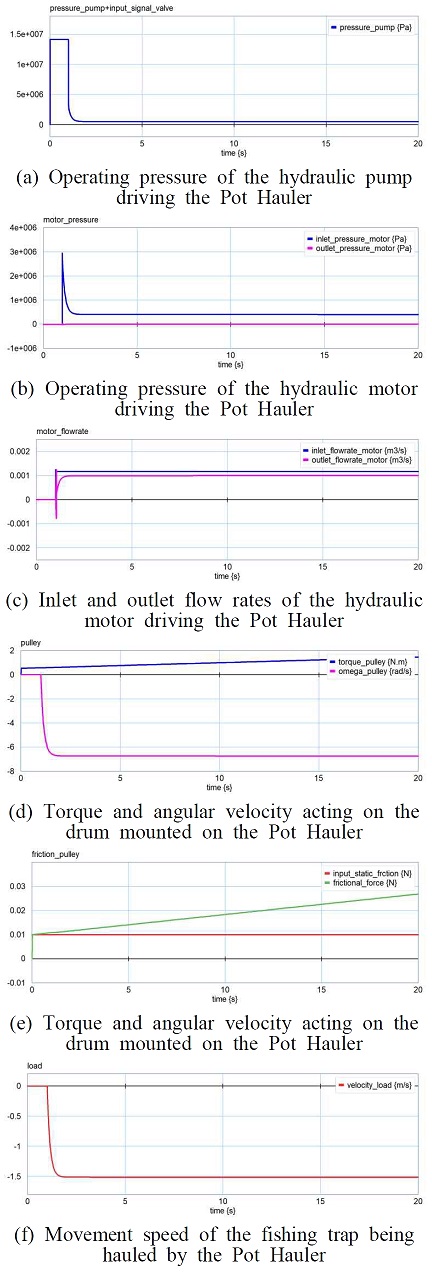
완성된 시뮬레이션 프로그램의 구성도와 수치해석 결과를 Fig. 6과 Fig. 7에 나타내었다.
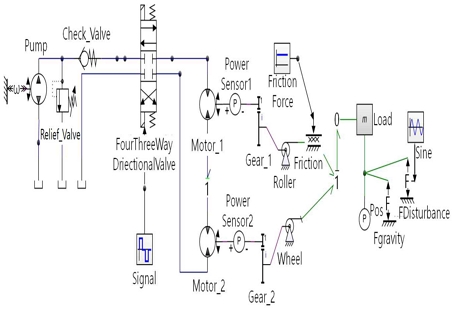
Mechanical and Hydraulic Configuration Diagram of the Pot Hauler Device for Modeling (20-sim Program)
3.2 수치해석 결과
양승기의 권양력이 처음 정상 상태에 수렴할 때의 결과 값들을 정리하여 Table 2에 나타내었다.
드럼과 줄 사이의 마찰력의 변화량을 조정하기 위하여 1, 2.5, 5, 7 N 사이의 외부 마찰력 값을 선정하고 부하력은 그물과 그 내용물을 합하여 최대 질량이 800 kg 작용할 때, 양승기에 작용되는 권양력, 권양 속도와 이때 드럼과 줄 사이에 발생되는 마찰력과 안정된 권양 속도가 발생되는 정상상태 시간 등을 계산하였다.
유압 장치의 시스템 압력은 14 MPa, 밸브 최대 개구 면적과 관로의 단면적은 1 inch로 산정하고 부하력은 7,840 N이 작용한다고 가정하고 수치해석을 수행하였다.
작업자가 줄을 드럼에 감기게 하는 힘인 외부 마찰력의 변화에 따라 드럼 동력과 드럼과 줄 사이의 내부 마찰력 및 권양 속도의 변화가 발생됨을 확인하였다. 또한 유압 장치의 펌프와 모터에 발생되는 압력의 변화에도 영향을 주는 것으로 계산되었다.
드럼에 인가되는 외부 힘에 의하여 양승기의 권양 속도가 달라짐을 확인하였으며, 권양 속도의 변화는 드럼 외부 마찰력이 1~7.5 N으로 인가될 때 권양 속도는 1.3~0.00658 m/s로 작아지는 결과를 얻었다. 이것은 드럼과 줄 사이의 마찰력의 영향에 의해 유압 모터에서 발생되는 토크는 커지나 상대적으로 회전 속도가 작아지기 때문이다. 유압 시스템에 사용되는 유압 펌프의 용량을 유압 모터의 용량보다 큰 것을 사용한다면 권양 속도의 범위를 확장할 수 있을 것으로 판단된다.
작업자가 줄을 드럼에 감을 때 발생되는 힘을 적절히 조절하여 작업을 하게 된다면 제안한 양승기 사양에서 충분한 권양력과 권양 속도를 얻을 수 있을 것으로 계산이 되었다.
이 연구에서 제안한 유압 장치의 제원이 원하는 권양력을 구현할 수 있었으며, 펌프 유량을 현재 제안한 배제 용량보다 큰 펌프를 선정함으로써 양승기의 권양 속도 범위를 확장할 수 있을 것으로 판단된다.
안정된 권양 속도가 나오는 시점은 외부 마찰력의 변화에도 불구하고 2.5 s 정도에서 안정된 상태를 유지하였다.
드럼 외부 마찰력이 7.5 N을 초과할 경우, 유압 모터에 작용하는 압력 변화가 역전되어 회전할 수 없어지므로 작업자가 적절한 힘으로 드럼에 줄을 감아야 할 것으로 판단된다.
4. 결 론
1) 양승기의 특성을 조사할 수 있는 수치해석 시뮬레이션 프로그램을 완성하였다.
2) 양승기에 사용되는 장치에 관한 수치 모델식을 본드선도를 이용하여 완성하였다.
3) 시뮬레이션 프로그램을 이용하여 얻은 수치해석 결과 다음과 같은 특성을 규명할 수 있었다.
유압 시스템 압력과 유량은 권양력의 크기에 직접적으로 영향을 미치므로 부하력의 크기가 어느 정도인지를 인지하는 것이 우선 선행되어야 할 것으로 판단되었다.
통발 양승기는 작업자가 줄을 드럼에 감기게 하는 힘인 외부 마찰력의 변화에 따라 드럼 동력과 드럼과 줄 사이의 내부 마찰력 및 권양 속도의 변화가 발생함을 확인하였고, 드럼에 인가되는 외부 힘에 의하여 양승기의 권양 속도가 달라짐을 확인하였으며, 권양 속도의 변화는 드럼 외부 마찰력이 1~7.5 N으로 인가될 때 권양 속도는 1.3~0.00658 m/s로 작아지는 결과를 얻었다. 또한 작업자가 줄을 드럼에 감을 때 발생되는 힘을 적절히 조절하여 작업을 하게 된다면 제안한 양승기 사양에서 충분한 권양력과 권양 속도를 얻을 수 있을 것으로 판단한다.
Acknowledgments
본 논문은 2024년 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임.(과제명: AI기반 어선안전 설계 데이터플랫폼 개발 및 실증)
Author contributions
O. D. Song and J. S. Park; Conceptualization. Y. W. Jeong; Data curation. O. D. Song and K. U. Yang; Formal analysis. O. D. Song; Investigation. J. S. Park; Methodology. J. S. Park; Project adminstration. J. S. Park; Resources. K. U. Yang; Software. O. D. Song; Validaton. Y. W. Jeong; Visualization. O. D. Song; Writing-original draft. J. S. Park; Writing-review & editing.
References
-
D. K. Choi and Y. Y. Kim, 2010, “Development of novel net hauler for improved washing of fishong nets”, KSME A, 34(11), 1779-1784.
[https://doi.org/10.3795/KSME-A.2010.34.11.1779]

-
M. S. Koo and S. J. Kim, 2014, “A study of the efficiency of the labor-saving-type, five-step-drum nethauler”, JFMSE, 26(1), 98-107.
[https://doi.org/10.13000/JFMSE.2014.26.1.98]

- H. M. Paynter, 1955, “Analysis and Design of Engineering Systems”, MIT Press. (http://hdl.handle.net/2027/mdp.39015064874921, )
-
S. Katsuya, 1999, “Pressure regulator valve by Bondgraph”, Simulation Modeling Practice and Theory 7, 603-611.
[https://doi.org/10.1016/S0928-4869(99)00024-5]

-
T. Jean, 1999, “Bondgraph and practical simulation”, Simulation Practice and Theory 7, 401-417.
[https://doi.org/10.1016/S0928-4869(99)00026-9]

- D. C. Karnopp, 2000, “System Dynamics”, John Willy & Sons, 12-423.
- D. C. Karnopp, D. L. Margolis and R. C. Rosenberg, 2001, “System dynamics: Modeling and Simulation of Mechatronic Systems, 3rd edn”, WILEY Interscience, Chichester.
-
A. Mashayekhi et al., 2022, “Analytical describing function of LuGre friction model”, International Journal of Intelligent Robotics and Applications, 6, 437-448.
[https://doi.org/10.1007/s41315-021-00220-0]

- J. S. Park and K. U. Yang, 2024, “Modeling of Spiral Net Hauler Device Using Bond Graph”, Journal of Fishing Village & Aquaculture, 4-2, 54-67.
- W. F. Riley / Sturges, L. D. John Wiley & Sons Inc, Translated by, Kim, Y. K., 1998, “Statics-Engineering Machanics”, 513-515.
- 20-sim, https://www.20sim.com, .