Design of Robust Decoupling Controller for 6-DoF Active Vibration Isolation System

2.1 System Description

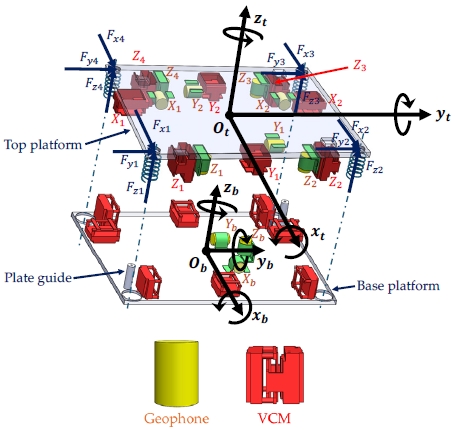
The diagram illustrating the proposed 6-DoF AVIS is presented in Fig. 1. The top platform, where high-precision devices operate, requires isolation from ground vibrations to maintain optimal device performance. The connection between the two platforms contains four vertical coil springs, serving to support the mass of the top platform. Eight voice coil motors (VCMs), responsible for controlling movement in 6-DoF, are arranged as illustrated in Fig. 1. Each VCM consists of two yokes moving linearly with each other. One yokes attaches to the lower face of the top platform, while the other attaches to the upper face of the base platform. Plate guides are implemented to restrict the movement of the top platform, ensuring the protection of VCMs.

Fig. 1

Schematic drawing of the 6-DoF AVIS

The top platform’s coordinate is defined as a right-handed system, in which the z_t-axis is pointing upward, the x_t-axis is pointing forward and the counterclockwise is the positive rotation direction. The origin of the top platform, denoted as O_t, is located at the center of mass of the top platform. The bottom platform’s coordinate system is defined in a similar manner.

The four vertical VCMs (Z₁, Z₂, Z₃, Z₄) produce linear forces in the z_t-direction. Additionally, the two horizontal VCMs (X₁, X₂) generate forces in the x_t-direction, while the other two horizontal VCMs (Y₁, Y₂) produce forces in the y_t-direction. The AVIS motion is monitored by 11 geophone sensors. On the top platform, eight geophone sensors correspond to eight VCMs. In the base platform, three sensors collect velocity in the x_b, y_b and z_b directions, respectively.

The control force of the actuators is denoted $$ {\mathit{U}}_{\mathit{a}}={\left[\begin{array}{c}{F}_{vx1}\hspace{0.25em}{F}_{vx2}\hspace{0.25em}{F}_{vy1}\hspace{0.25em}{F}_{vy2}\hspace{0.25em}{F}_{vz1}\hspace{0.25em}{F}_{vz2}\hspace{0.25em}{F}_{vz3}\hspace{0.25em}{F}_{vz4}\hfill \end{array}\right]}^T$$, where

• F_vx1, F_vx2: linear forces in the x_t-direction;

• F_vy1, F_vy2: linear forces in the y_t-direction;

• F_vz1, F_vz2, F_vz3, F_vz4: linear forces in the z_t–direction.

The dimension of the AVIS is defined as below:

• l_vjni; j, n = x, y, z; i = 1,...,4: distance from the actuator j_i to the center of mass of the top platform in the n_t-direction;

• l_ni; n = x, y; i = 1,...,4: distance from the spring i to the center of mass of the top platform in the n_t-direction;

• l_z: distance along the z_t-direction from the center of mass of the top platform to the bottom face of the top platform;

• l, w, h: length, width, and height of the top platform respectively.

2.2 System Dynamics

To design a proper controller for a 6-DoF AVIS, the dynamics of the system must be analyzed. The system dynamics can be expressed by the following equation:^1-2,9)

where:

• $$ {\mathit{x}}_{\mathit{t}}={\left[\begin{array}{cccccc}{x}_t\hfill & y_t\hfill & z_t\hfill & {\theta }_{xt}\hfill & {\theta }_{yt}\hfill & {\theta }_{zt}\hfill \end{array}\right]}^T$$: the motion vector of the top platform, θ_xt, θ_yt, θ_zt: rotations about x_t-, y_t-, and z_t-axes of the top platform.

• $$ {\mathit{x}}_{\mathit{b}}={\left[\begin{array}{cccccc}{x}_b\hfill & y_b\hfill & z_b\hfill & {\theta }_{xb}\hfill & {\theta }_{yb}\hfill & {\theta }_{zb}\hfill \end{array}\right]}^T$$: the ground vibration vector, θ_xb, θ_yb, θ_zb: rotations about the x_b-, y_b-, and z_b-axes of the bottom platform.

• $$ {\mathit{U}}_{\mathit{v}}={\left[\begin{array}{cccccc}{F}_{vx}\hfill & F_{vy}\hfill & F_{vz}\hfill & M_{\theta x}\hfill & M_{\theta y}\hfill & M_{\theta z}\hfill \end{array}\right]}^T$$: the control vector in 6-DoF. F_vj is the total control force in the corresponding j_t-direction, M_θj is the total control torque in the j_t–direction.

The coefficient matrices of equation (1) are given by:

in which:

• $$ \left\{\begin{array}{c}{a}_1=\left(l_{x1}+l_{x2}-l_{x3}-l_{x4}\right)\hfill \\ a_2=\left(l_{y1}^2+l_{y2}^2+l_{y3}^2+l_{y4}^2\right)\hfill \\ a_3=\left(l_{x1}^2+l_{x2}^2+l_{x3}^2+l_{x4}^2\right)\hfill \end{array}\right.$$,

• m: the sprung mass;

• k_j, c_j; j = x, y, z: stiffness and damping ratio of the spring along the j_t-direction assume that the springs act as linear springs;

• J_j; j = x, y, z: the inertia tensor element of the sprung mass in the corresponding j_t–direction with the assumption that the inertia tensor matrix is diagonal.

2.3 System Transfer Matrix

The system dynamics can be transformed into the state-space form as equation (3):

in which

• $$ \mathit{X}={\left[\begin{array}{cc}{\mathit{x}}_{\mathit{t}}^{\mathit{ }T}\hfill & {\dot{\mathit{x}}}_{\mathit{t}}^{\mathit{ }T}\hfill \end{array}\right]}^T$$: the state vector;

• $$ \mathit{Y}={\dot{\mathit{x}}}_{\mathit{t}}$$: the system output vector;

• $$ {\mathit{X}}_{\mathit{b}}={\left[\begin{array}{cc}{\mathit{x}}_{\mathit{b}}^{\mathit{ }T}\hfill & {\dot{\mathit{x}}}_{\mathit{b}}^{\mathit{ }T}\hfill \end{array}\right]}^T$$: the vector of vibrations from the bottom platform.

The coefficient matrices of equation (3) are given by:

where 0_6×6 denotes the 6-by-6 zero matrix, I_6×6 denotes the 6-by-6 identity matrix.

By applying equation (5), the transfer function matrix of the system (3) is obtained in the following form of equation (6):¹⁰⁾

In equation (6), G_ii(s), i = 1,...,6, are the transfer functions in the diagonal line of G(s). That is, G_ii(s) is the ratio between the Laplace transform of the velocity in the i^th direction and the Laplace transform of the applying force/torque in this direction. G_in(s), i = 1,...,6, i ≠ n, are the remaining other transfer functions. In other words, G_in(s) are the transfer functions of the interferences. These interferences act as internal disturbances, affecting the performance of the system.

3.1 Feedforward Control Law

To begin with, from equation (6), the system can be rewritten as follows:

in which [G_ii(s)] is the diagonal matrix from the diagonal line of G(s) and [G_in(s)] is the matrix containing the remainder. It is noted that (7) only exists if the transfer function G_ii(s)^-1G_in(s) is proper and analytic functions for every i and n.¹⁰⁾ Additionally, by defining U_k(s) = H(s)U_v(s), equation (7) becomes:

U_k(s) acts as the control input for the system of the diagonal elements [G_ii(s)], i.e, the system without interferences. Then, once the control input U_k(s) is obtained, and if H(s) is invertible, U_v(s) can be obtained by:

Besides, from equation (7), U_v(s) can be equivalently written as follows:

in which U_f(s) is the feedforward element.

In equation (10), one can see that for each DoF of the AVIS, the total control input consists of the corresponding control for the system without interference and the feedforward control from the inputs of the interacting directions. Therefore, the feedforward eliminates the mutual interferences among the movements.

3.2 Feedback Control Law

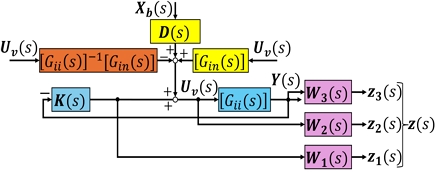
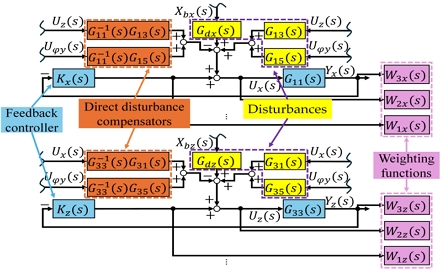
In this study, the mixed sensitivity H_∞ control is applied for designing U_k(s), thanks to its effectiveness and efficiency in handling complex systems with uncertainties.^11-13) Fig. 2 illustrates the configuration of the control for the entire 6-DoF AVIS. Fig. 3 demonstrates how the controller works for each DoF of the system. In which, K(s) is the feedback control transfer matrix, and W₁(s), W₂(s), W₃(s) are the proper and analytic frequency-dependent weighting functions. It is noted that the mutual interferences between each channel are eliminated by the use of feedforward. Nevertheless, these compensators themselves are considered disturbances to the system. Hence, the weighting function W₁(s) is chosen corresponding to the control effort without the feedforward compensator. W₂(s) is to suppress the total disturbances. W₃(s) corresponds to the system outputs. The functions are selected based on the system characteristics and designer experience, ensuring each exceeds the corresponding maximum singular values in the system. Then, the closed-loop transfer function can be expressed as:^11-14)

Fig. 2

Schematic drawing of the proposed control for 6-DoF AVIS

Fig. 3

Schematic drawing of the proposed control for the xt- and zt-directions of the AVIS

where:

• $$ \mathit{S}\left(s\right)={\left({\mathit{I}}_{\mathbf{6}\times \mathbf{6}}+\left[G_{ii}\left(s\right)\right]\mathit{K}\left(s\right)\right)}^{-1}$$ ;

• $$ \mathit{T}\left(s\right)=\left[G_{ii}\left(s\right)\right]{\left({\mathit{I}}_{\mathbf{6}\times \mathbf{6}}+\left[G_{ii}\left(s\right)\right]\mathit{K}\left(s\right)\right)}^{-1}$$;

• W_i(s), i = 1, 2, 3, are diagonal:

The mixed sensitivity problem can be described as finding K(s) to stabilize the closed-loop system and minimizing the H_∞ norm of M(s).^11-14) The resulting controller matrix K(s) is in the following form:

in which K_j(s) is the controller corresponding to the j_t-direction, j = x, y, z, θ_x, θ_y, θ_z. The complete control law of the AVIS is written by:

Then, the control forces U_a of the eight actuators can be simply obtained as follows:

4.1 System Implementation

The algorithm implementation of the proposed controller is described in the following steps: (1) The system parameters are determined; (2) The feedforward control is constructed as in equation (10); (3) The H_∞-based controller is computed by using the function ‘mixsyn’ in Mathworks MATLAB; and (4) The order of the controller is reduced using the balanced truncation method with the focus frequency range is from 0.01 to 100 [Hz]. Additionally, a PID controller are designed for the AVIS for comparison:

in which K_P, K_I, K_D are diagonal matrices of parameters of the PID controller for each DoF. The parameters of the PID controller are selected by trial-and-error method with the assistance of the PID Tuner app in Mathworks MATLAB. The response time is 0.002s, the rise time is at most 0.00218, the settling time is at most 0.0164s, and the overshoot is at most 10.5%. The parameters of the 6-DoF AVIS and the PID controllers are respectively listed in Tables 1 and 2. Additionally, the weighting function matrices W_i(s) are listed in Appendix.

Table 1

Platforms specifications

Table 2

PID controllers’ parameters

4.2 Simulation Results

The simulation is carried out using MATLAB/Simulink. The performance is tested by the chirp signal, which denotes the vibration from the ground. The chirp signal has amplitude of 0.001 [m/s] and a frequency range span from 0.01 to 100 [Hz]. Moreover, the controller also needs to handle mutual interferences from other directions.

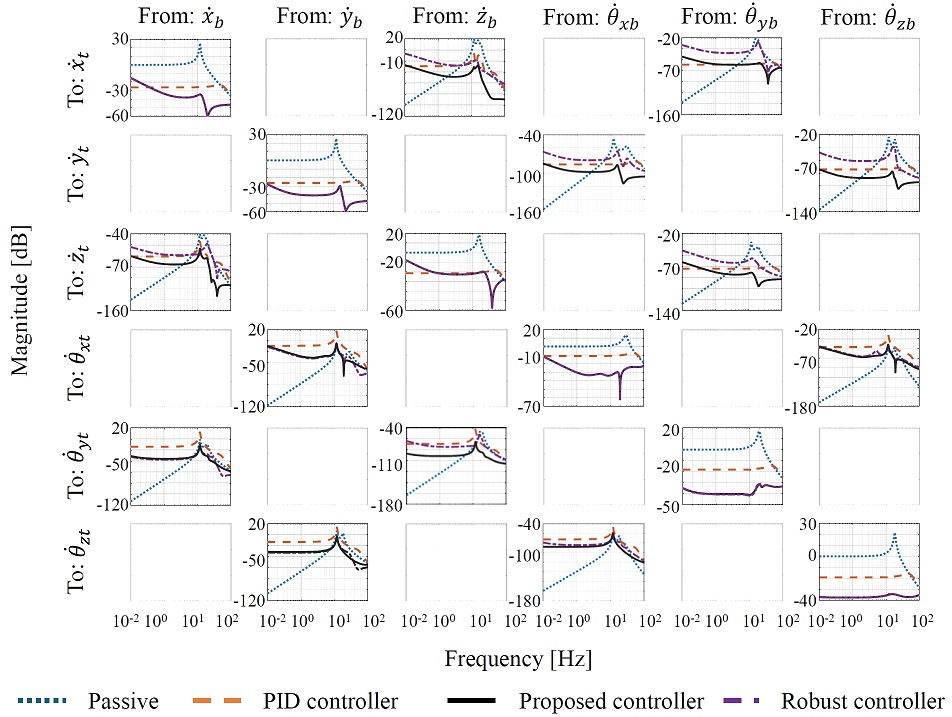
Fig. 4 shows the vibration isolation results in all directions using an array of the frequency responses – the Bode plots. The row represents ground vibration ($$ {\dot{\mathit{x}}}_{\mathit{b}}$$), while the column represents the motion of the top platform ($$ {\dot{\mathit{x}}}_{\mathit{t}}$$). Each plot in the diagonal line is the frequency response of the system in one direction corresponding to the ground vibration in the same direction. The remainders in the figure represent the effect of the disturbances other directions. For instance, for a ground vibration in the x_b-direction, the responses of the top platform are shown in the first column in the figure. The first graph is the frequency response also in the x_t-direction. The other two graphs are the motion in the z_t and θ_yt-direction.

Fig. 4

Frequency responses of top platform

The passive system, the spring-mass-damper system, can suppress the vibration in the high-frequency but suffers from an unwanted phenomenon, the resonant peak in the diagonal element. This resonant peak occurs at a frequency of around 20 [Hz], amplifies rather than suppresses vibrations. The robust decoupling controller provides a good vibration isolation performance over all frequencies. For the interferences, the proposed controller has an effect in a range of frequencies, around 15 to 80 [Hz]. The robust controller without feedforward and PID controller also proves to be efficiency in the main direction, as evident from the six graphs along the diagonal line in the Fig. 4. In these instances, it effectively suppress the vibration and stabilizes the top platform against the disturbance from the ground. However, when it comes to the interference suppression, the robust controller and PID controller proves ineffective. This is particularly noticeable in the non-diagonal graphs of the Fig. 4. In comparison with the proposed controller, the PID controllers is not effective enough in most of the frequencies, even in the main direction, where the PID controller achieves the most vibration isolation performance. In the interference suppression, the PID controller almost has no effect, making it less effective than the proposed controller, which works well across a wider range of frequencies. On the other hand, the robust controller without the feedforward maintains almost identical performance in the main direction in comparison with the robust decoupling controller, however, the results of the interference direction are not effective as the proposed controller especially in the translational motions.

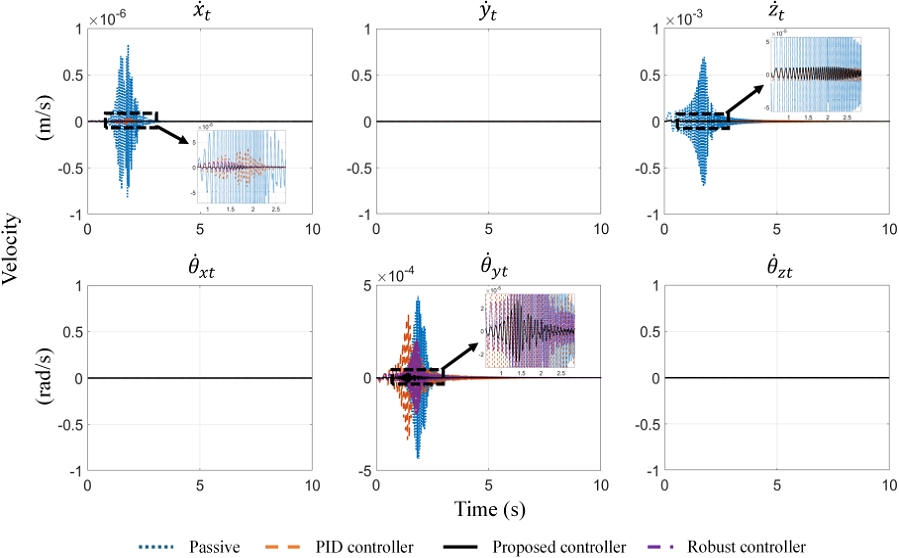
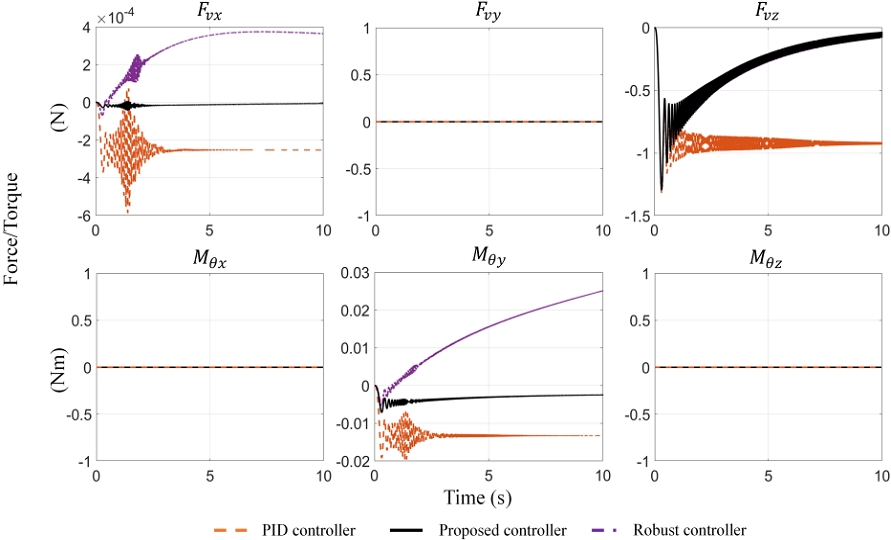
To further clarify the vibration isolation performance, the vibration isolation results in case of ground vibration in the z_b-direction only is presented in Fig. 5. In the translational direction x_t and z_t, the PID controller has an impressive effect on stabilizing the top platform, indicating in the velocities $$ {\dot{x}}_t$$ and $$ {\dot{z}}_t$$ in the first and third graphs. However, the PID controller is not as effective as the robust decoupling controller. In the rotational direction $$ {\dot{\theta }}_{yt}$$, the PID controller performance is far from the performance of the robust decoupling controller. The velocities in case of PID controller are the least impressive, following by the robust controller without feedforward and the best results are the robust decoupling controller. The velocities in the remaining graphs $$ {\dot{y}}_t$$, $$ {\dot{\theta }}_{xt}$$ and $$ {\dot{\theta }}_{zt}$$ are very small. Fig. 6 represents the control effort of the PID controller, the robust controller and the robust decoupling controller. During the initial one second, the control efforts of the three controllers are closely align. However, beyond this point, the proposed controller seems to be more responsive to the disturbance than the remaining controllers. Consequently, the PID controller proves to be less effective. The control efforts of the robust decoupling controller are smallest compares with the PID controller and the robust controller. The control efforts in the remaining graphs F_vy, M_θx and M_θz are very small (approximately 10^-16).

Fig. 5

The velocities at the center of the top platform in case of disturbance in zb-direction

Fig. 6

The control effort of the controllers – robust decoupling controller, robust controller, and PID controller - in case of disturbance in zb-direction.

Author contributions

Y. B. Kim; Conceptualization, Supervision and Project administration. D. H. Lee; Investigation and methodology. T. N. Nguyen; Software, formal analysis, data curation, visualization, writing-original draft. T. Huynh; Conceptualization, methodology, validation, writing-review & editing. T. N. Nguyen and T. Huynh contributed equally to this work.