접이안 상황을 고려한 바지선 운동제어에 관한 연구

1. 서 론

해상작업 대부분은 파랑 등의 자연환경에 노출된 상황에서 수행된다. 이러한 환경에서 석유시추나 탐사목적으로 고정된 플랫폼을 이용하기도 하지만 부유식 형태의 플랫폼도 이용된다. 또한 해상플랫폼에는 이동이 용이한 선박형태로부터 수행해야 할 작업의 다양성에 적절히 대응하기 위해서는 다양한 도구와 방법도 필요하다. 그러한 요구로 도입된 것 중의 하나가 바지선이고, 현재까지 다양한 목적으로 상당히 효과적으로 활용되고 있다. 단순히 이송을 목적으로 사용되는 것이 일반적이나, 회전형 추진장치를 탑재하여 이동성과 조종성을 극대화함으로써 상당히 정교한 작업이 가능하여 고정형 플랫폼과 같은 성능을 확보할 수도 있다. 이것은 지극히 특수한 경우이고, 모래 운반이나 조선소 현장에서 거대블록형 자재를 이송하는 목적으로 사용하는 것이 일반적이다.

이러한 경우에는 대부분 예선으로 끄는 형식으로 작업을 수행해야 하며, 자체 추진장치가 없어 원하는 조종성능을 기대할 수 없다. 즉 예선의 도움으로 조종성을 확보할 수는 있으나 자체 추진장치를 활용하는 경우보다 높은 작업 완성도를 얻는다는 것은 거의 불가능하다. 그럼에도 불구하고 예선의 도움은 반드시 필요하다.^1-5) 예를 들어, 중대형 선박이 접안을 시도하는 경우에는 선박 자체 추진장치가 있음에도 불구하고 예선 지원은 필수적인 것이 현실이다. 이것은 복잡한 항만 내에서의 작업 안전성을 확보하기 위해서이고, 자체 추진장치를 갖지 않은 바지선 형태의 경우에는 더더욱 예선의 지원이 필요하게 된다. 이 경우에도 작업형태에 따라 예선배치는 달라지고 상황에 따라 실시간으로 그 위치도 변경해야 작업 안전성이 보장된다.

그래서 본 연구에서는 접안하거나 이안하는 경우에 있어서 예선을 배치하는 방법과 그에 따른 제약조건을 고려한 제어계설계법에 대해 고찰한다. 예선을 활용한 수상선박의 제어방법에 대해서는 이미 여러 가지 제어기법을 적용한 사례가 있다. 적응형 제어기 설계법,⁶⁾ 슬라이딩 모드 제어기법과 유전알고리즘을 결합한 형태의 제어기법 도입 등,⁷⁾ 4척의 예선으로 구성한 제어시스템을 대상으로 다양한 제어기법을 적용한 사례가 있다. 그러나 위에 소개한 연구결과는 예선배치에 관한 제약이 없이, 해상에서 단순히 바지선을 완만하고 직선적인 경로로 견인하거나, 예선을 선박에 장착된 추진장치의 하나로 간주한 경우이다.^2-8) 따라서 예선과 예인되는 선박간에 발생하는 물리특성을 제대로 반영하지 않았기 때문에 시뮬레이션 결과에 대한 신뢰성이 결여되었다고 할 수 밖에 없다. 따라서 본 연구에서는 바지선의 실제 운용환경을 적절히 반영한다는 관점에서, 제어대상과 예선의 운동특성 및 선박간 상호작용 등의 물리적 특성을 고려하여 모델링을 수행하고 제어계를 설계한다. 그리고 시뮬레이션을 통해 제안하는 제어전략과 제어기법의 유효성을 검증하도록 한다.

2. 견인 로프의 물리특성을 고려한 시스템 모델링

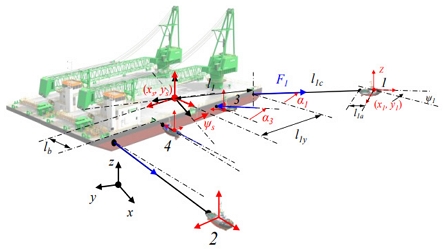
서론에서 기술하였듯이 본 연구의 최종목표는 4척의 예선으로 바지선을 설정된 위치로 정확하게 이동시키는데 있다. 이를 위해서는 예선을 방사형으로 배치시키는 것이 일반적이나, 안벽으로 접근하는 경우에는 모든 예선을 한쪽 편으로 배치할 수밖에 없다. 따라서 바지선을 기준으로 개방된 해상측 뿐만 아니라, 안벽측과 같이 어느 한쪽이 닫혀진 상황에도 적절히 대응하기 위해서는 Fig. 1과 같이 예선을 배치하는 것이 타당하다. 그래서 본 논문에서는 Fig. 1과 같이 설정된 시스템을 제어대상으로 하여 모델링을 수행하도록 한다. Fig. 1에 나타낸 바지선과 예선에 대한 운동특성은 다음 식으로 표현할 수 있다.

Fig. 1

Schematic configuration of an adopted offshore platform transportation system

여기서 k = s, 1, 2는 바지선, #1 예선, #2 예선을 의미하며, M_k∈R^3×3는 관성행렬, D_k∈R^3×3는 댐핑행렬이다. η_k = [x_k, y_k, ψ_k]^T ∈R³는 지구고정좌표계에서의 선박위치와 선수각, ν_k는 물체고정좌표계에서의 속도벡터이다. 따라서 두 좌표계 간의 관계는 회전행렬 R(ψ_k)를 통해 정리된다.

또한 벡터 τ_k = [τ_kx, τ_ky, τ_kψ]^T는 바지선 선체에 작용하는 서지방향 힘, 스웨이방향 힘과 요우모멘트를 나타낸다. 이러한 힘은 예선이 바지선을 미는 힘과 끄는 힘으로 만들어진다. 그래서 이 힘들의 생산과 작용관계는 Fig. 1에 나타낸 것과 같다고 하면 작용력 τ_s는 다음과 같이 정리할 수 있다.

여기서 F_i(i = 1,...,4)는 i번째 예선이 밀거나 댕기는 힘을 의미한다. 이때 F_i ≥ 0라는 제약조건이 주어지는데, 이것은 Fig. 1에 나타낸 것과 같이 예선 추력은 한 방향으로만 바지선에 전달된다는 것을 말한다. 그리고 α_i는 바지선 측면에서 예선이 접촉하는 점, 로프 연결점에서의 법선과 각 예선 무게중심이 이루는 각도이며, 그림으로부터 그 관계를 쉽게 이해할 수 있다.

그리고 l_iy, l_b는 Fig. 1에 나타낸 것과 같이 바지선 무게중심과 예선 추력 작용점 사이의 거리이다. 또한 c(•) = cos(•), s(•) = sin(•)와 같이 간단히 표시한다.

바지선 운동제어를 위해 제어기로부터 계산된 제어력은 위의 식 (2)를 통해 4척의 예선으로 분배된다. 이때 시스템 구성상, 2척은 바지선에 접촉하고 2척은 로프로 연결되어 있어 제어력 전달특성이 각각 다를 수밖에 없다. 즉 바지선에 접촉한 상태로 미는 역할을 하는 #3, #4 예선 추력은 거의 그대로 바지선에 전달된다고 한다.

반면 로프로 연결된 #1, #2 예선 발생 추력은 로프의 물리특성 때문에 전자와는 다르게 전달될 것이다.

그래서 본 연구에서는 #3, #4 예선 제어를 위한 제어력은 식 (2)로부터 분배가 이루어진다고 가정하고, #1, #2 예선에 대해서는 로프 특성 등을 고려하므로 보다 구체적이고 면밀하게 그 힘들을 분배하도록 한다. 그래서 바지선을 끌어당기는 힘(F_i, i = 1,2)은 예선 추력과 로프 장력에 의해 바지선에 전달되며, 그 관계를 다음 식으로 표현한다.

일반적으로 바지선과 예선이 로프로 연결된 견인 시스템에서는, 선박에 설치된 윈치로 견인력을 조절하며, 이러한 경우에도 제어계를 적절히 설계함으로써 바람직한 제어성능을 달성할 수 있다.⁵⁾

그러나 로프 인장특성 등을 고려한다면 반드시 그러한 결과를 얻는다는 보장은 없다. 따라서 신축과 팽창특성을 고려하면 로프로 연결하여 당기는 견인력은 다음과 같이 표현할 수 있다.

여기서 k와 b는 각각 로프의 강성계수와 감쇠계수이다. δ_li는 로프의 길이변화, s(δ_li)는 로프가 인장될 경우에만 나타나는 힘을 반영하기 위해 도입한 smooth 함수이다. 이때

와 같고, l_i는 바지선 무게중심에서 바지선 측 로프 연결점까지의 거리, l_ia는 예선 무게중심에서 예선측 로프 연결점까지의 거리이며, Fig. 1로부터 확인할 수 있다.

3. 예선 제어를 위한 최적 제어력 분배

바지선 등 해상플랫폼을 이동하기 위한 예선배치는 다양한 형태로 구성할 수 있다. 그럼에도 불구하고, 앞서 기술한 것과 같이 모든 예선을 예인대상 선박의 한쪽에만 배치하여 예인하는 경우만 고려한다. 이렇게 할 경우, 제어기로부터 계산된 제어신호는 식 (2)에 따라 각각의 액추에이터로 할당되게 된다. 그러나 액추에이터에 해당하는 예선을 Fig. 1과 같이 한쪽으로만 배치해야 하는 특수한 경우, 즉 제어력의 작용방향에 대한 제약 0 ≤ F_i ≤ F_th와 예선 선수각 변동범위에 대한 제약조건 α_min ≤ α_i ≤ α_max이 지켜진다는 보장이 없다. 따라서 이러한 제약조건을 만족하면서 제어력이 적절히 분배되도록 하는 제어력 분배방법을 제안한다. 이를 위해 먼저 식 (2)를 다음과 같은 비선형함수로 변형하여 표현한다.

이때 s는 최소화해야 할 변수이고, τ_sd를 τ_s의 목표값으로 설정한다. 그리고 두 번째 최적화 벡터를 z = [ΔF^T, Δα^T, s^T]^T라 정의한다.

여기서 ΔF = F_d - F, Δα = α_d - α이고, F_d, α_d는 각각 F, α의 목표값이라 둔다. 식 (6)의 우항에 대한 근사화는 Taylor 급수전개법으로 근사화할 수 있다. 따라서 제어력분배는 다음식으로 주어지는 최적화문제⁹⁾로 귀착된다.

여기서 H∈R^11×11는 2차형식 목적항(quadratic objective term)으로 정정대칭행렬이며, h∈R¹¹는 또 하나의 목적항으로 선형벡터이다. 그 외 위 식에 포함된 행렬과 벡터는 다음 식과 같다.

식 (7)에 나타낸 최적화문제는 수치연산을 통해 쉽게 그 해를 찾을 수 있다. 결론적으로 목표로 하는 제어력분배 결과값은 다음과 같이 구해진다.

4. 로버스트 협조제어계 설계

4.2 로버스트 제어기 설계

열악한 해상환경 및 시스템표현에서의 불확실성을 고려한다면 당연히 로버스트 제어기법으로 제어계를 설계해야 한다.

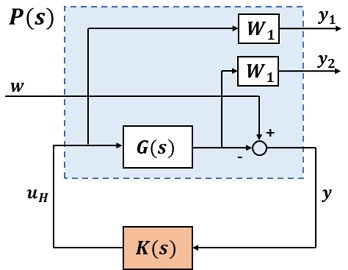
대표적인 것이 Fig. 2에 나타낸 H_∞제어기법이며, 이것을 기반으로 하여 예인선 제어를 위한 제어기를 설계한다. Fig. 2에서 G(s)는 제어대상, P(s)는 일반화 플랜트, K(s)는 설계해야 할 제어기를 나타낸다.

Fig. 2

H∞ control framework

여기서 w는 바지선과 예선의 상태에 대한 기준값, 즉 목표로 하는 상태값으로 정의하고, 다음 식으로 나타낸다.

$\[ \begin{array}{c}\mathit{w}={\left[\begin{array}{ccc}{\mathit{\eta }}_{sd}^T\hfill & {\mathit{z}}_{1d}^T\hfill & {\mathit{z}}_{2d}^T\hfill \end{array}\right]}^T\hfill \\ {\mathit{\eta }}_{sd}^T={\left[\begin{array}{ccc}{x}_{sd}\hfill & y_{sd}\hfill & {\psi }_{sd}\hfill \end{array}\right]}^T\hfill \\ {\mathit{z}}_{id}^T={\left[\begin{array}{ccc}{\alpha }_{id}\hfill & {\psi }_{id}\hfill & l_{ic}+\gamma \hfill \end{array}\right]}^T, i=\mathrm{1,2}\hfill \end{array} \]$

(14)

이때 (x_sd, y_sd, ψ_sd)는 바지선의 위치 및 선수각에 대한 목표값을 의미한다. 그리고 (α_id, ψ_id)는 끌어당기는 각 예선의 목표선수각 및 바지선에 대한 상대각의 목표값을 나타낸다.

또한 γ는 로프의 장력을 원하는 값으로 유지하기 위해 반영하는 양의 스칼라 값이다. Fig. 2에서 W₁, W₂는 외란 및 불확실성의 특성을 고려하여 도입하는 중량함수(weighting function)이다.

이러한 준비로부터 일반화 플랜트는 식 (15)와 같이 간단히 표현할 수 있게 된다.

$\[ \left[\begin{array}{c}\dot{\stackrel{-}{\mathit{x}}}\hfill \\ {\mathit{y}}_1\\ {\mathit{y}}_2\\ \mathit{y}\end{array}\right]=\left[\begin{array}{ccc}\mathit{A}& \mathbf{0}& \mathit{B}\\ \mathbf{0}& \mathbf{0}& {\mathit{W}}_1\\ {\mathit{W}}_2\mathit{C}& \mathbf{0}& \mathbf{0}\\ -\mathit{C}& \mathit{I}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\overline{\mathit{x}}\\ \mathit{w}\\ \mathit{u}\end{array}\right] \]$

(15)

이것으로부터 로버스트 제어기 설계법에 기반하여 제어기를 설계한다.

식 (15)로 표현된 제어대상에 대한 H_∞제어기 설계목표는, 이미 잘 알려져 있는 것과 같이 외부입력(w)에서 제어출력z(y₁, y₂, y)까지의 전달함수(T_zw)에 대해 ∥T_zw∥_∞ < γ (>0)로 주어지는 제약조건을 만족하는 제어기 K(s)를 구하는 것이다.

제어기K(s)가 구해지면, 제어기를 통해 계산되는 제어신호는 $$ \mathit{u}={\left[\begin{array}{c}{\mathit{\tau }}_{sd}^T, {\mathit{\tau }}_{1d}^T, {\mathit{\tau }}_{2d}^T\hfill \end{array}\right]}^T$$가 된다. τ_sd는 기본적으로 식 (2)에 따라 원하는 상대각도 α_d와 힘 F_d를 계산하는데 이용된다. 그리고 로프에 연결된 예선에 대한 제어신호는

$\[ {\mathit{\tau }}_{Ti}={\mathit{\tau }}_{id}+{\mathit{B}}_i{\mathit{F}}_{id}, i=\mathrm{1,2} \]$

(16)

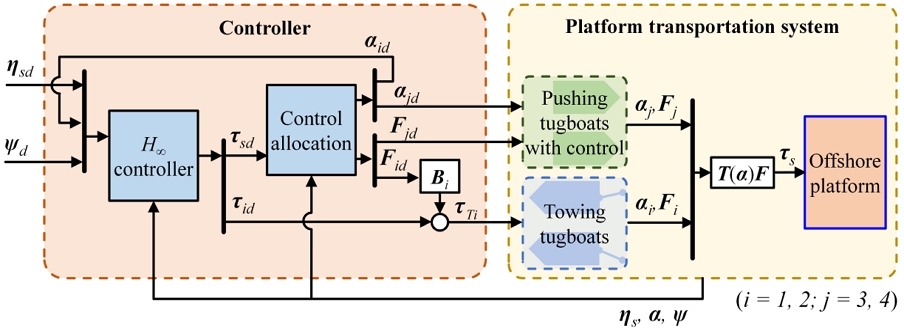
와 같이 구해진다. 따라서 전체 제어시스템에서의 신호의 흐름과 제어력이 어떻게 작용하는지는 Fig. 3을 통해 확인할 수 있다.

Fig. 3

Schematic drawing of designed control system

5. 시뮬레이션

제안된 제어전략과 제어계의 성능검증을 위해 시뮬레이션을 실시하였다. 이동해야 할 제어대상 바지선은 추지장치가 없는 실험용 선박이며, 4척의 예선은 동일한 규격⁴⁾의 것을 이용하였다. 그리고 #1, #2 예선과 바지선을 연결하는 로프 물리특성, 제어력분배 최적화 문제에 이용한 목적항과 제약조건 등은 Table 1에 정리하였다. 아울러 제어기 설계 시 도입한 중량함수도 Table 1 하단에 표기하였다. 이러한 준비 아래 제어기를 설계하고 설정된 경로를 따라 정해진 위치로 바지선을 이동시키는 시뮬레이션을 실시하였다. 이때 이동구간은 크게 두 구간으로 나누었다. 즉 0~300 s와 300~500 s 시간영역에서 이동경로를 달리하였으며, 이것은 선박이 항내로 진입하여 안벽으로 평행이동하는 상황을 고려한 것이다. 이것을 수식으로 표현하면 첫 번째 이동구간에서의 경로와 목표 선수각은

Table 1

Specifications and conditions for simulation

와 같고, 두 번째 이동구간에서의 이동경로와 목표 선수각은 다음과 같이 설정하면 된다.

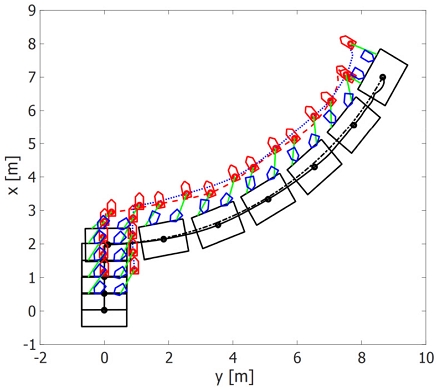
이동 시작 지점은 좌표상에서 (10 m, 10 m)이고, 최종적으로는 (1 m, 0 m)에서 정지하도록 설정하였다. 시뮬레이션결과로 식 (17)과 식 (18)로 주어진 경로를 따라 이동하는 바지선과 예선의 운동특성을 Fig. 4에 나타내었다. 점선이 설정된 이동경로이며, 설정경로를 따라 바지선이 양호하게 잘 추종한다는 것을 확인할 수 있다. 그림에서 큰 사각형이 바지선, 청색 오각형이 #3, #4 예선, 그리고 붉은색 오각형이 바지선에 로프(초록색)로 연결된 #1, #2 예선이다.

Fig. 4

Trajectories of the transported platform and the tugboats

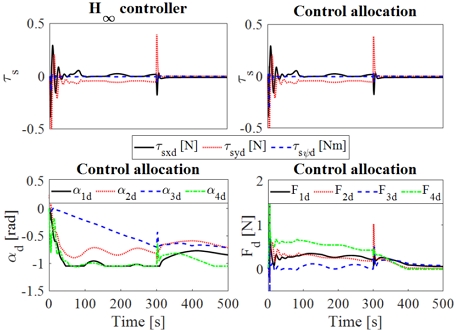
또한 Fig. 5에는 제어기로부터 계산된 제어신호와 이것의 제어력분배결과를 나타내고 있다. 좌측 상단은 제어기로부터 계산된 제어신호 τ_sd, 이것을 최적화 기법으로 구한 제어력분배 결과값이 우측상단이 된다. 제어기로부터 계산된 제어신호가 이상적인 값, 즉 목표값이 되며, 식 (2)를 통해 4척의 예선이 실행해야 할 바지선에 대한 각 예선의 상대각도 α_id(i = 1,...,4)와 제어력 F_id를 Fig. 5의 하단 좌측과 우측에 각각 나타내었다. 그림으로부터 알 수 있듯이, 예선 추력에 대한 제약조건 F_th ≤ 2[N]과 선수각변동범위에 대한 제약조건 -π/3 ≤ α_i ≤ π/3 [rad]을 만족하고 있다.

Fig. 5

Results of optimal control allocation

앞서 설명한 것과 같이 바지선에 접촉한 상태로 제어력을 전달하는 #3, #4 예선은 제어기에서 계산된 제어력을 그대로 바지선에 전달한다고 가정한다. 반면 로프로 연결되어 일정 거리(0.7 m)를 유지하면서 운동하는 예선 #1, #2는 로프의 장력변동 등으로 제어력을 그대로 바지선에 전달할 수 없다.

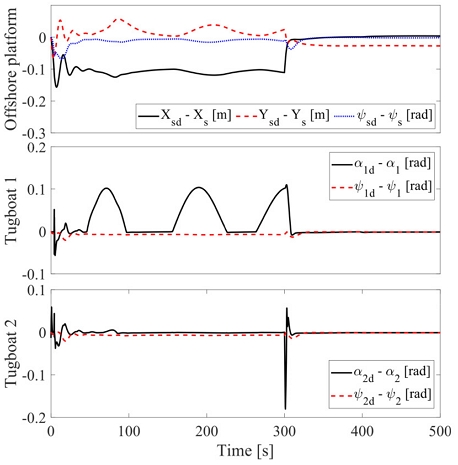
따라서 이러한 점을 고려한 경우와 그렇지 않은 경우의 시뮬레이션결과에는 차이가 있을 수밖에 없다. 그 결과를 나타낸 것이 Fig. 6이다. 그림에서 제일 상단이 바지선 운동특성에서의 오차(위치 및 선수각), 그 아래가 #1 예선에서의 상대각도와 선수각 오차, 제일 하단이 #2 예선 운동특성에서의 오차를 각각 나타낸다.

Fig. 6

Tracking errors

6. 결 론

본 논문에서는 바지선 형태의 해양플랫폼을 안전하고 정교하게 이동하기 위한 새로운 운동제어방법을 제안하였다.

제어대상인 바지선에는 어떠한 액추에이터 기능이 없고, 4척의 예선 제어를 통해 이동할 수 있는 상황이라 설정하였다. 이것은 예선배치방법 중에서도 가장 난이도가 높은 접이안 상황을 고려한 것이며, 이에 대한 가장 효과적인 제어전략을 제시한 것이다. 특히 바지선에 접촉한 상태로 추력을 전달하는 예선과 달리, 로프로 연결된 예선은 로프 장력변화에 따른 추력전달특성이 다르다는 사실을 모델링과 제어기 설계문제에 충실히 반영하였다.

이러한 준비 아래 로버스트 제어기법으로 제어기를 설계하여 불확실성이 존재하는 상황에 대응하도록 하였으며, 최적화 기법에 따라 제어력을 분배하는 방법도 제안하였다. 이러한 방법과 전략에 대한 유효성과 우수성을 시뮬레이션을 통해 검증하였다.

Acknowledgments

본 논문은 부경대학교 자율창의연구비(2023년)지원사업으로 수행된 결과임.

References

• Z. Du, V. Reppa and R. R. Negenborn, 2020, “Cooperative Control of Autonomous Tugs for Ship Towing”, IFAC-PapersOnLine, 53(2), 14470-14475. [https://doi.org/10.1016/j.ifacol.2020.12.1448]
• V. P. Bui and Y. B. Kim, 2011, “Development of Constrained Control Allocation for Ship Berthing by Using Autonomous Tugboats”, International Journal of Control, Automation and systems, 9, 1203-1208. [https://doi.org/10.1007/s12555-011-0622-4]
• M. G. Feemster and J. M. Esposito, 2010, “Comprehensive Framework for Tracking Control and Thrust Allocation for a Highly Overactuated Autonomous Surface Vessel”, Journal of Field Robotics, 28(1), 80-100. [https://doi.org/10.1002/rob.20369]
• D. H. Lee, T. Huynh, Y. B. Kim and J. S. Park, 2022, “Motion Control System Design for Barge-Type Surface Ships Using Tugboats”, Journal of Marine Science and Engineering, 10(10), 1-15. [https://doi.org/10.3390/jmse10101413]
• Z. Du, R. R. Negenborn and V. Reppa, 2023, “Distributed Dynamic Coordination Control for Offshore Platform Transportation Under Ocean Environmental Disturbances”, IEEE Transactions on Control Systems Technology, 31(5), 2093-2106. [https://doi.org/10.1109/TCST.2023.3291557]
• V. P. Bui, H. Kawai, Y. B. Kim and K. S. Lee, 2011, “A Ship Berthing System Design with Four Tugboats”, Journal of Mechanical Science and Technology, 25, 1257-1264. [https://doi.org/10.1007/s12206-011-0215-4]
• S. M. Lee, J. H. Lee, M. I. Roh, K. S. Kim, S. H. Ham and H. W. Lee, 2021, “An Optimization Model of Tugboat Operation for Conveying a Large Surface Vessel”, Journal of Computational Design and Engineering, 8(2), 654-675. [https://doi.org/10.1093/jcde/qwab006]
• D. H. Lee, S. Chakir and Y. B. Kim, 2020, “Control System Design for Vessel Towing System by Activating Rudders of the Towed Vessel”, International Journal of Naval Architecture and Ocean Engineering, 12, 943-956. [https://doi.org/10.1016/j.ijnaoe.2020.11.008]
• F. Scibilia and R. Skjetne, 2012, “Constrained Control Allocation for Vessels with Azimuth Thrusters”, 45(27), 7-12. [https://doi.org/10.3182/20120919-3-IT-2046.00002]