The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 27, No. 6, pp.67-78

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 31 Dec 2023

Received 23 Oct 2023 Revised 29 Nov 2023 Accepted 05 Dec 2023

DOI: https://doi.org/10.9726/kspse.2023.27.6.067

두 원형분류의 45° 상호 충돌로 혼합된 난류 유동장의 대규모 와 모사

김장권^*^{, †}

*교수, 국립군산대학교 ONSE대학 기관공학 전공

Large Eddy Simulation of Turbulent Flow Fields Mixed by 45° Collision of Two Circular Jets

Jang-Kweon Kim^*^{, †}

*Professor, Major of Marine Engineering, College of ONSE, Kunsan National University.

Correspondence to: ^†Jang-Kweon Kim : Professor, Major of Marine Engineering, College of ONSE, Kunsan National University. E-mail : flowkim@kunsan.ac.kr, Tel : 063-469-1848

초록

본 연구는 두 원형분류를 수평으로 상호 45° 충돌시켰을 때 형성된 충돌분류를 대규모 와 모사로 해석하여 그 값을 실험값과 비교 분석하였다. 유동 반폭의 분포는 충돌력의 영향이 강하게 나타나는 1.0≤X/X₀≤2.0에서는 동적 Smagorinsky 모델과 WALE 모델이 절댓값으로 최대 약 25% 이내의 오차율을 보이나, X/X₀>2.0 이후에서는 동적 Smagorinsky 모델이 절댓값으로 최대 약 6.5% 이내의 오차율로 가장 우수하다. 또 동적 Smagorinsky 모델로 해석한 평균속도 및 난류운동에너지는 수평축 및 수직축 방향의 거리 증가에 따라 충돌력이 강하게 지배하는 1.0≤X/X₀≤2.0에서는 실험값과 차이를 보이지만, 그렇지 않을 때는 서로 잘 일치한다. 난류운동에너지는 충돌점 근처에서 가장 크게 발달한다. 결과적으로 두 원형분류를 45°로 충돌시켰을 때 형성된 충돌분류를 대규모 와 모사로 완벽하게 해석하기에는 여전히 부족하나, 충돌분류의 분포 경향을 모사하기에는 충분하다고 판단된다.

Abstract

In this study, the collision jets formed when two circular jets collided horizontally at 45° to each other were analyzed using large eddy simulation, and the values were compared and analyzed with experimental values. As for the distribution of flow half-width, in the region of 1.0≤X/X₀≤2.0 where the impact of collision force is strong, the dynamic Smagorinsky model and WALE model show an error rate of up to about 25% in absolute value; however, the dynamic Smagorinsky model is the best with an error rate of up to about 6.5% in absolute value in the region of X/X₀>2.0. The mean velocity and turbulent kinetic energy analyzed by the dynamic Smagorinsky model differ from the experimental values in the region of 1.0≤X/X₀≤2.0 where the collision force is strongly dominated as the distance in the horizontal and vertical axes increases, but otherwise they agree well with each other. Turbulent kinetic energy develops the greatest near the collision point. As a result, it is still insufficient to perfectly interpret the collision jet formed when two circular jets collide at 45° through large eddy simulation, but it is judged to be sufficient to simulate the distribution tendency of the collision jet.

Keywords:

Impinging Jet, Large Eddy Simulation (LES), Half-Width, Mean Velocity, Turbulent Kinetic Energy

키워드:

충돌분류, 대규모와 모사, 반폭, 평균속도, 난류운동에너지

1. 서 론

충돌분류(collision jet or impinging jet)는 교차분류(cross jet)나 스월유동(swirling flow)과 더불어 난류 유동을 촉진해 유체의 혼합 과정을 극대화하기 때문에 굴뚝의 매연을 효율적으로 대기 속에 분출시켜 주변의 오염을 줄인다거나, 전자 기판의 부품이나 가스터빈 날개 등에서 발생하는 열을 효율적으로 냉각시킨다거나, 내연기관이나 연소장치 내에 연료나 공기를 효율적으로 분사시킨다거나, 연소실 내의 화염 속에 2차 공기량을 효과적으로 투입하는 등에 활용할 수가 있어 그 응용 범위는 매우 넓다고 볼 수 있다.

지금까지 두 원형분류(round jet)를 일정 각도인 45°로 정지 상태인 유동 공간에 상호 충돌시켜 형성된 충돌분류는 주로 Rho 등^1-4)에 의해서 실험적으로 연구되었다. 여기서 Rho 등^1-4)은 충돌분류의 난류 유동장을 X형 열선풍속계로 측정하여 속도분포, 난류강도 및 난류전단응력 등을 통해 유동 확산과정을 규명하였다. 한편, Kim 등^5,6)은 실험으로 부족한 충돌분류의 난류 유동장 정보를 더 고찰하기 위해 CFD 해석으로 이론적인 연구를 한 바가 있다. 여기서 Kim 등^5,6)은 상용프로그램인 Fluent(ver. 6.3)를 이용하여 RANS (Reynolds-Averaged Navier-Stokes) 방정식의 난류 모델로 Standard k-ε, Realizable k-ε, SST k-ω들을 적용하여 중심선 상의 유동축(X) 방향 평균속도 성분의 분포와 수평축(Y) 및 수직축(Z) 방향으로 확산하는 유동 반폭(half-width)들을 각각 이미 발표된 실험 결과^1-4)들과 비교한 결과, 난류 소산율을 늦추기 위해 소산율 수송방정식의 계수를 수정한 Realizable k-ε난류 모델이 그나마 특정 구간⁶⁾에서 실험값과 가장 잘 일치함을 알 수 있었다.

한편, Jones 등⁷⁾은 수평 덕트를 흐르는 주 유동에 수직으로 공기의 평면 제트(plane jet)를 분사하여 얻어진 교차분류를 모사하기 위해 대규모 와 모사(LES, Large Eddy Simulation) 기법을 사용하였으며, Majander 등⁸⁾은 수평으로 흐르는 주 유동에 수직으로 원형분류를 분사하여 형성된 교차분류에 대해 LES를 적용하였다. 또 Wegner 등⁹⁾은 난류 혼합을 증대시킬 방법을 모색하기 위해 흘러오는 주 흐름에 원형분류의 각도를 변화시켜 충돌시켰을 때 발생하는 교차분류에 대해 LES를 적용하였다. 또 Propovac 등¹⁰⁾은 전자부품의 냉각 사례를 조사하기 위해 평면 채널(channel)의 바닥 면에 5개의 상자를 일렬로 부착한 다음 가열된 중앙부 상자를 냉각하기 위해 채널을 흐르는 공기흐름에 채널 상부로부터 수직으로 원형분류를 분사시켰을 때 형성된 교차분류를 해석하기 위해 LES를 적용하였다. 이처럼 이미 발표된 LES를 적용한 논문들^7-10)은 주 흐름에 분류를 별도로 충돌시키는 교차분류에서 주로 이루어졌음을 알 수 있다. 그러나 두 원형분류를 일정 각도인 45°로 수평 상태에서 상호 충돌시켜 형성된 충돌분류에 대해서는 LES가 적용된 바가 없어, 이번 충돌분류의 수치 연구에서는 LES 기법을 적용하여 유동장의 특징을 파악하고자 한다.

LES 기법¹¹⁾은 유동 형상에 덜 민감하며, 비정상상태에서 해의 정확도가 높다고 잘 알려져 다양한 분야의 유동 해석에 적용되고 있음을 알 수 있다. 이 LES 기법¹¹⁾은 다양한 크기의 척도(scale)를 갖는 난류 와(eddy)들에 의해 조직화된 난류 유동을 정확히 해석하기 위해 주어진 격자(mesh) 크기의 필터(filter)보다 더 큰 대규모 와(large scale eddy)는 어떠한 가정이나 모델들 없이 직접 계산하고, 필터보다 더 작은 소규모 와(small scale eddy)는 아격자 척도(SGS, Sub-Grid Scale)라는 난류 모델을 도입하여 해를 구하는 방법이다.

이번 연구에서는 수평축과 수직축으로 발달해가는 충돌분류의 유동 반폭을 이용하여 LES의 3가지 SGS 난류 모델들이 예측한 값들과 실험값들^1-4)을 상호 비교하여 충돌분류와 가장 잘 일치하는 SGS 난류 모델을 찾고자 하며, 이를 토대로 충돌분류에 대한 유동장의 특징들을 실험값과 자세히 비교 검토하고자 한다. 이를 위해 이번 연구의 LES 해석에서는 유한체적법에 기초한 상용소프트웨어인 SC/Tetra¹¹⁾를 사용하였다.

2. 수치해석

2.1 해석모델

LES는 격자의 형상비(aspect ratio)에 매우 민감해하므로 각 방향으로 향한 격자 크기는 벽에 수직인 방향으로 향한 크기와 일치하여야 하므로 엄청난 양의 격자 요소(element)가 필요하다. 따라서 해의 정확성과 안정성을 확보하기 위해선 격자 요소의 크기가 분해할 수 있는 난류 와의 크기에 밀접하게 연관되기 때문에, 격자의 미소 크기와 균일한 형상비만 확보된다면 LES가 RANS보다도 더 정확하게 난류 운동의 미소 크기들을 포착할 수 있다.¹¹⁾

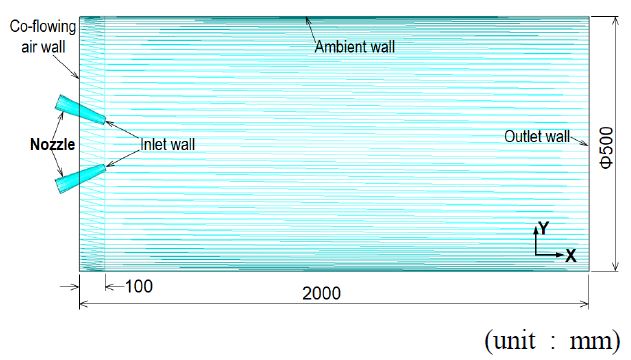
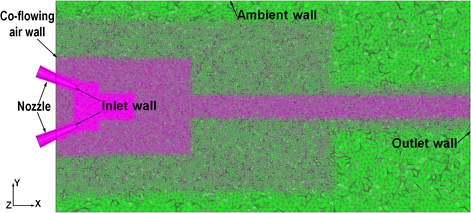
Fig. 1은 두 원형분류가 45°로 상호 수평으로 충돌하였을 때, 충돌분류가 확산 발달하여 타원형의 유동장을 형성하는 모습을 나타내고 있다. 또 Fig. 2는 Fig. 1의 충돌분류를 해석하기 위해 외란이 없는 정지 상태인 유동장 공간에 두 원형분류를 45°로 상호 충돌시켜 형성된 자유 충돌분류를 해석하기 위한 수치모델의 그림이다. 여기서 교차한 노즐들을 감싸기 위해서는 반경이 500 mm이고, 길이가 2,000 mm인 원통형 덕트를 이용하였으며, 노즐 출구면을 기준으로 상류측 유동 영역으로는 100 mm, 하류측 유동 영역으로는 1,900 mm가 분리되도록 해석 영역을 설정하였다. 또 Fig. 3은 Fig. 2의 해석모델을 계산하기 위해 만들어진 비정형 격자(unstructured mesh) 형상이다. 이 형상은 상용소프트웨어인 SC/Tetra¹¹⁾의 전처리 소프트웨어를 이용하여 표면 각각에 경계조건들을 부여한 다음, 격자 크기를 제어하는 "Octree" 기능을 이용하여 원통 외곽표면에서 중심선 쪽으로 갈수록, 또 두 원형분류가 충돌하여 얻어진 기하학적 충돌지점(cp) 부근으로 갈수록 격자를 더 작게 세분화하여 만들었다. 이와 같은 격자 생성으로 얻어진 요소 총수와 교점(node) 총수 그리고 최대격자 크기와 최소격자 크기는 Table 1과 같다. 또 유체와 접하는 원통형 노즐 내부 벽면들의 표면에는 해의 수렴성을 높이기 위해 SC/Tetra에서 기본적으로 주어지는 모두 2개의 프리즘 층(prism layer)을 넣었다.

Fig. 1

Geometry and flow structure of 45° impinging jet [unit : mm]1-4)

Fig. 2

Analysis model for 45° impinging jet(unit : mm)

Fig. 3

Mesh configuration for 45° impinging jet

Table 1

Mesh characteristics of Fig. 3

2.2 수치기법

이번 충돌분류의 해석모델에서 적용한 노즐은 마찰력을 갖는 점착(no-slip) 조건으로 설정하였으며, 노즐 출구를 빠져나오는 원통 벽면을 입구(inlet wall)로 하여 속도 40 m/s를, 그리고 노즐을 감싸는 정지 상태인 원통 입구의 벽면(co-flowing air wall)은 노즐의 공기 분출로 Entrainment 효과를 발휘하도록 속도 0 m/s와 정압 0 Pa을 적용하였으며, 원통 외곽표면의 벽(ambient wall)은 마찰력이 없는 Free-slip으로 정하였다. 또 원통 출구 벽면(outlet wall)은 대기압조건으로 정압 0 Pa를 설정하였다. 한편, 노즐 출구속도 40 m/s는 20℃기준 레이놀즈수로 5.2×10⁴이다.

이번 LES 해석에서 사용한 SGS 모델¹¹⁾에는 SM(Smagorinsky model)과 DSM(dynamic Smagorinsky model) 및 WALE(wall-adapting local eddy-viscosity) 모델이 있다. 또 시간 미분 항은 2차 음함수기법(2^nd order implicit scheme)을, 또 대류 항은 2차 중앙차분기법(2^nd order central difference scheme)을 각각 적용하였다.¹¹⁾ 또 이산화된 방정식들의 압력보정에는 모두 SIMPLEC 알고리듬을 사용하였다. 한편, LES에 필요한 초기시간 간격(initial time step)은 노즐 출구의 속도 40 m/s와 최소격자 크기를 고려하여 1.7×10^-5초로 정하였으며, 어떠한 시간 간격(time interval)에도 해석 결과에 영향을 받지 않기 위해 꾸랑수(Courant number)¹¹⁾는 1로 정하였다. 이를 토대로 질량유량(mass flux)이 충분히 안정을 보이면서 3.4초에 해당하는 20만 회까지 비정상상태로 해석하고, 다시 이를 토대로 추가로 20만 회를 앙상블(emsemble) 평균 계산하여 수치 결과를 얻었다.

3. 계산 결과 및 고찰

3.1 유동 반폭을 통한 해석모델의 비교

Fig. 4는 Fig. 1의 Y=Z=0인 노즐 출구면으로부터 X축 방향의 위치변화에 따라 발달하는 X-Y평면의 유동 반폭 b₁의 분포를 LES의 SGS모델에 따라 해석한 결과를 실험값과 비교하여 오차율과 함께 나타낸 그림이다. 여기서 유동 반폭 b₁은 각 X축 중심선상의 위치에서 얻어진 X축 방향 평균속도 성분(U)의 최댓값을 절반으로 하는 크기를 갖는 Y축 방향의 좌우 유동장 위치를 보간법을 통해 각각 구한 다음 평균화하여 얻었다. 또 오차율은 해석값과 실험값의 차이를 해석값으로 나누어 계산하였다. 또 실험값은 X선 열선풍속계로부터 얻은 지난 연구^1-4)의 결과를 사용하였다.

Fig. 4

Comparisons of half-width developed in the X-Y plane

Fig. 4(a)에서 LES로 해석한 Y축 방향의 유동 반폭 b₁은 충돌력이 강하게 지배하는, 즉 두 노즐의 원형분류가 충돌하여 혼합이 강하게 유지되는 약 1.0≤X/X₀≤2.0의 초기영역에서는 LES의 DSM과 WALE의 절댓값 기준 해석값이 실험값과 최대 약 25% 이내 오차율의 예측 성능을 보여 주나, X/X₀>2.0 이후에서는 LES의 DSM이 실험값과 약 5% 이내 오차율로 가장 잘 일치하고 있다.

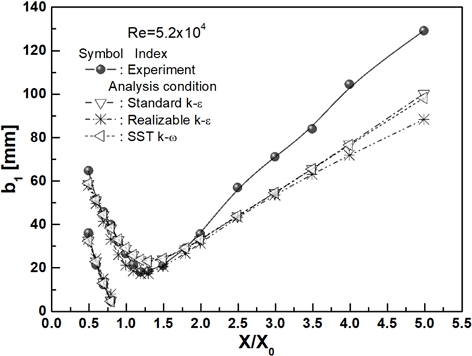
반면에 Fig. 5는 지난 연구^5,6)에서 상용소프트웨어인 FLUENT로 RANS 모델들을 이용하여 해석한 결과들을 유동 반폭 b₁의 실험값과 비교한 그림이다. 여기서 유동 반폭 b₁은 X/X₀<2.0까지는 LES의 경우와 같이 해석값이 실험값과 작은 차이를 보이고 있지만, X/X₀>2.0 이후에서는 모든 난류모델의 해석값이 실험값보다 현저히 작은 크기 분포로 큰 오차들을 나타내고 있다.

Fig. 5

Comparisons of half-width developed in the X-Y plane5,6)

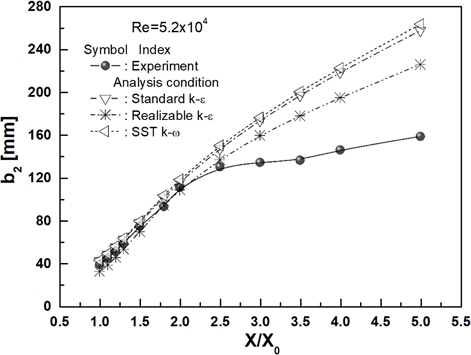
Fig. 6은 Fig. 1의 Y=Z=0인 노즐 출구면으로부터 X축 방향의 위치변화에 따라 발달하는 X-Z평면에서 형성된 유동 반폭 b₂의 분포를 LES의 SGS모델에 따라 해석한 결과를 실험값과 함께 비교한 그림이다. 여기서 유동 반폭 b₂는 앞서 언급한 유동 반폭 b₁이 얻어진 과정과 같다. LES로 해석한 Z축 방향의 유동 반폭 b₂는 DSM과 WALE 모델의 해석값이 SM 모델보다 전 영역에 걸쳐 실험값과 더 잘 일치하나, X/X₀<2.0 이내에서는 DSM과 WALE이 각각 절댓값 기준 최대 약 25%와 15% 이내의 오차율을 보여 주나, X/X₀>2.0 이후에서는 DSM 모델이 최대 약 6.5% 이내의 오차율로 실험값과 가장 잘 일치하고 있다. 반면에 Fig. 7은 지난 연구^5,6)에서 FLUENT의 RANS 모델로 해석하여 얻은 유동 반폭 b₂를 실험값과 비교한 그림이다. 여기서 유동 반폭 b₂의 해석값은 LES의 경우와 같이 X/X₀≤2.0까지는 실험값과 작은 차이를 보이고 있지만, X/X₀>2.0 이후에서는 모든 해석값들이 실험값보다 현저히 크게 예측함을 알 수 있다. 결과적으로 유동 반폭 b₁과 b₂를 통해 LES의 DSM 모델의 해석값이 다른 모델들보다 실험값과 가장 잘 일치함으로 이후 분석에서는 LES의 DSM으로 해석한 결과들을 실험값과 비교하였다.

Fig. 6

Comparisons of half-width developed in the X-Z plane

Fig. 7

Comparisons of half-width developed in the X-Z plane5,6)

3.2 평균속도 분포

Fig. 8은 두 원형분류의 45° 상호 충돌로 형성된 충돌분류의 3차원 공간에서 같은 크기를 갖는 X축 방향의 평균속도 성분의 등표면(iso-surface) 분포를 나타낸 그림이다. 여기서 Fig. 8(e)와 같이 충돌이 형성되는 X₀ 부근에서는 노즐 출구속도에 절반의 크기가 형성되고, X축 방향 평균속도 성분이 감소함에 따라 Y축 방향보다는 Z축 방향으로 훨씬 더 확산 발달하는 모습을 보여 주고 있다. 이것은 두 노즐이 Y축 방향에서만 수평으로 45° 충돌하므로 Y축 방향에서는 충돌력이 강하게 지배되는 X축 영역(1.0<X/X₀<2.0)까지는 최소 유동폭의 영역을 거친 후 확산하여 발달하지만, Z축에서는 직접적인 충돌력이 존재하지 않아 충돌점(X₀) 이후부터 Y축의 유동보다 훨씬 더 크게 확산하여 발달하기 때문이다. 따라서 각 X축의 위치에서 Y-Z단면에서 형성되는 유동은 타원형과 같은 형상을 갖게 된다.^5,6)

Fig. 8

Iso-surface profiles of axial(X-axis) mean velocity component (U) obtained by LES (DSM)

Fig. 9는 X-Y평면의 각 X축 방향의 위치에 따라 LES(DSM)로 해석한 X축 방향의 평균속도 성분을 Y축 방향의 거리에 따라 나타낸 그림이다. 여기서 X축 방향의 평균속도 성분은 노즐 출구속도(U₀)로 무차원화 했으며, Y축 방향의 거리는 노즐 출구직경(d_o)으로 무차원화 하였다. 먼저 X-Y 평면의 X/X₀=0.5는 두 원형분류가 45°로 충돌하기 이전의 위치지만 충돌의 영향이 상류 쪽으로도 전해지므로 주 분류의 X축 방향 평균속도 성분의 해석값은 실험값과 어긋나 분포하나 최댓값은 서로 비슷한 크기를 갖는다. 그러나 X/X₀= 0.5 이후 이어진 X축 방향 하류의 거리에서 X축 방향 평균속도 성분의 해석값은 X/X₀=2.5까지는 최댓값을 포함한 속도가 센 Y축 방향의 위치에서 실험값보다 같거나 더 작은 크기로 분포되나 X/X₀=3.0 이후부터는 실험값과 거의 일치하고 있다. 이것은 X/X₀=2.5까지는 두 원형분류의 충돌력이 영향을 미치지만, LES가 이를 제대로 해석하지 못해 발생한 현상으로 보이며, X/X₀=3.0 이후부터는 두 원형분류가 충분히 혼합되므로 충돌력의 영향이 낮아져 제대로 해석하는 것으로 판단된다. 특히 이런 현상은 Realizable k-ε로 해석한 지난 연구^5,6)에서도 비슷한 결과를 얻은 바 있다.

Fig. 9

Axial mean velocity component (U) profiles developed in the X-Y plane

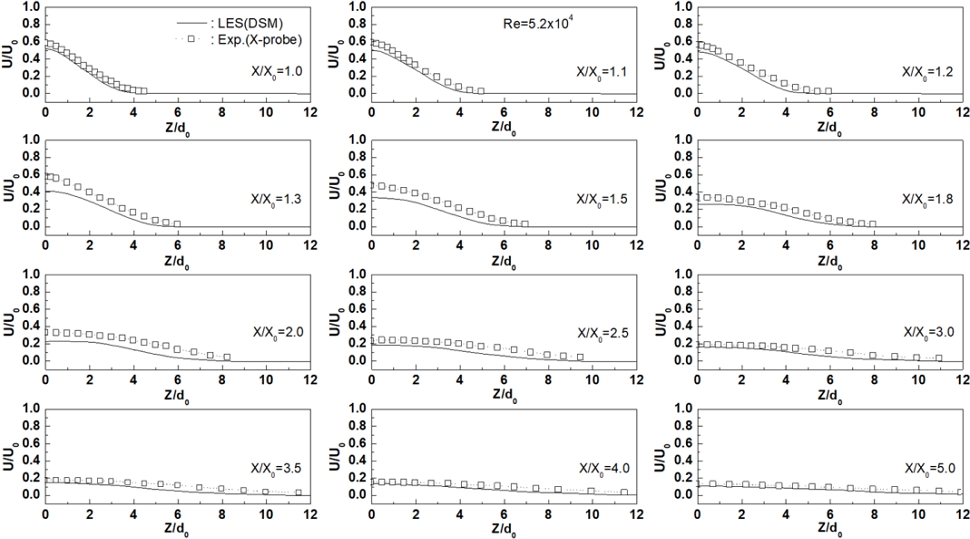
Fig. 10은 X-Z평면의 각 X축 방향의 위치에 따라 LES(DSM)로 해석한 X축 방향의 평균속도 성분을 Z축 방향의 거리에 따라 나타낸 그림이다. 여기서도 X축 방향의 평균속도 성분과 Z축 방향의 거리를 각각 U₀와 d₀로 무차원화 하였다. X축 방향의 평균속도 성분의 해석값은 X/X₀=2.5까지는 전반적으로 실험값보다 작은 크기 분포를 보이나, X/X₀=3.0 이후로 갈수록 서로 잘 일치하고 있다. 이것 역시 앞서 설명한 두 원형분류의 충돌로 인해 충돌력이 강한 영역에서는 LES가 정확히 예측하지 못하지만, 충돌력이 약해진 영역 이후부터는 정확히 예측함을 알 수 있다.

Fig. 10

Axial mean velocity component (U) profiles developed in the X-Z plane

3.3 난류운동에너지 분포

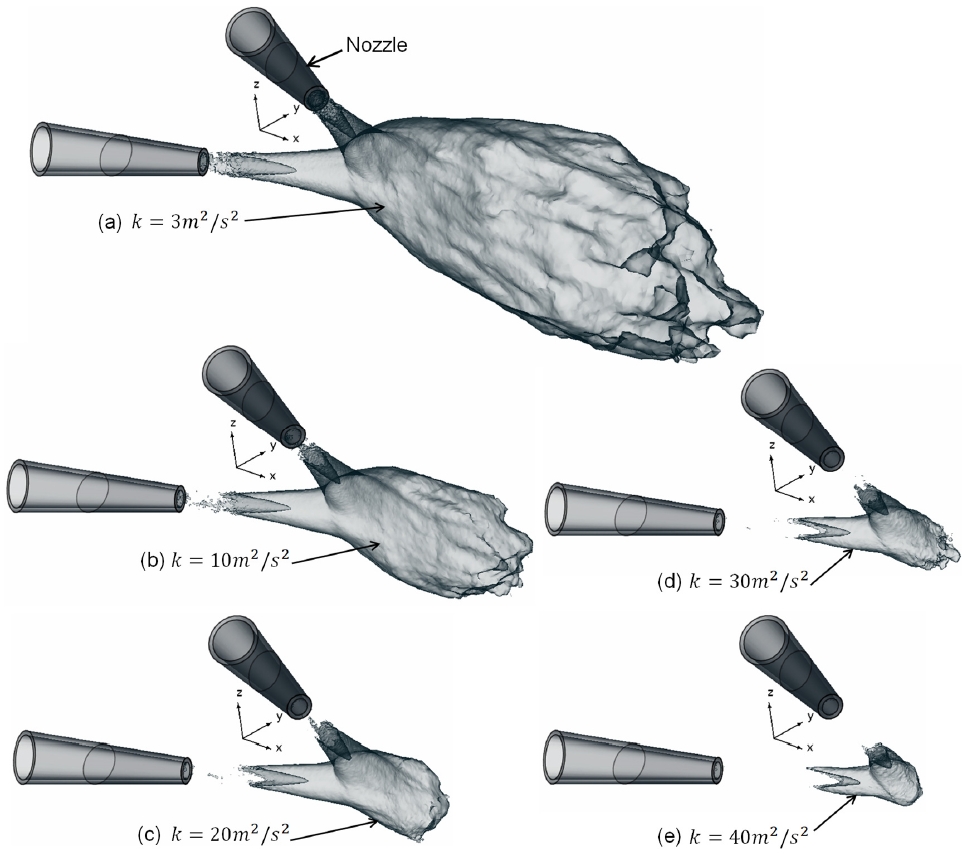
Fig. 11은 두 원형분류의 45° 상호 충돌로 형성된 충돌분류의 3차원 공간에서 같은 크기를 갖는 난류운동에너지(k)의 등표면(iso-surface) 분포를 나타낸 그림이다. 난류운동에너지의 크기가 k=3 m²/s²과 같이 작으면, 노즐 출구로부터 형성하여 하류로 길게 뻗어 타원형^5,6) 체적의 형상으로 확산 발달한 모습을 보인다. 그러나 난류운동에너지의 크기가 점차 증가하면, 노즐 출구에서 벗어난 하류 영역에서 발달하며, 특히 두 원형분류의 충돌점 근처 영역에서 가장 크게 발달함을 알 수 있다. 따라서 크기가 작은 난류운동에너지는 하류까지 멀리 확대되어 나타나지만, 최대 난류운동에너지는 충돌점 근처에서 집중됨을 알 수 있다.

Fig. 11

Iso-surface profiles of turbulent kinetic energy (k) obtained by LES (DSM)

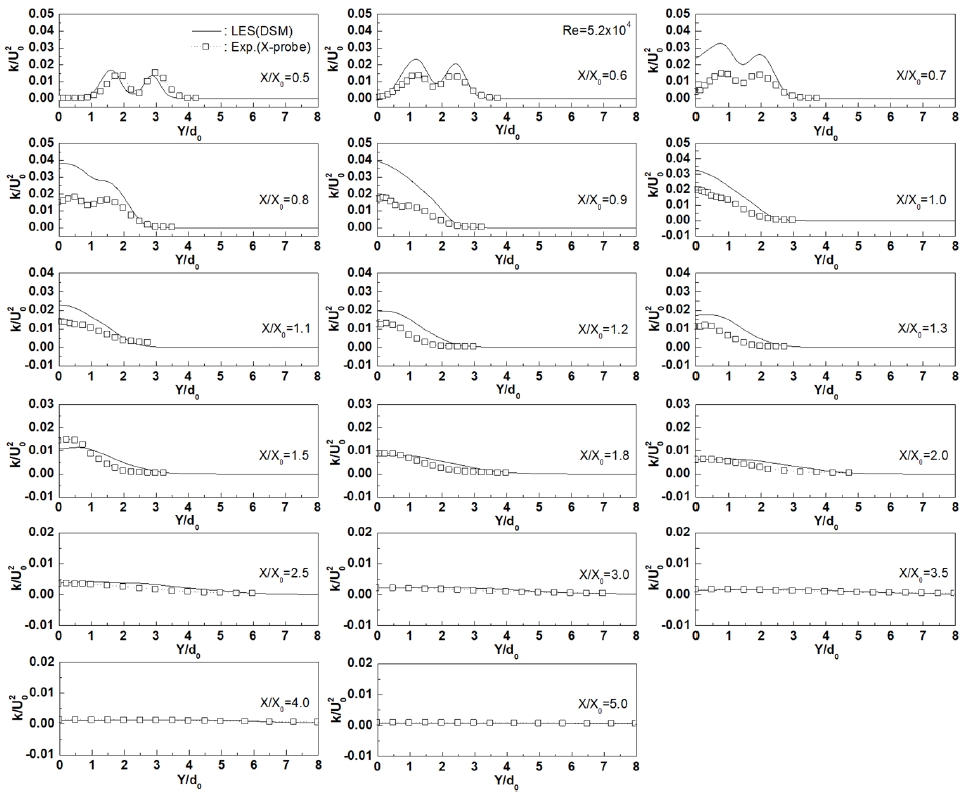
Fig. 12는 X-Y평면의 각 X축 방향의 위치에 따라 LES(DSM)로 해석한 난류운동에너지를 Y축 방향의 거리에 따라 나타낸 그림이다. 여기서 난류운동에너지는 노즐 출구속도(U₀)의 제곱으로 무차원화 했으며, Y축 방향의 거리는 노즐 출구직경(d_o)으로 무차원화 하였다. X-Y평면에서 형성된 난류운동에너지의 LES 해석값은 전체적으로 실험값과 유동 분포 경향을 공유하나 그 크기는 특히 0.6≤<X/X₀≤1.3의 영역에서 실험값보다 크게 예측하며, 충돌력이 강하게 지배하는 영역에서는 LES라도 제대로 대응하지 못함을 알 수 있다. 이것 역시 Realizable k-ε으로 해석한 지난 연구^5,6)에서도 같은 현상을 얻은 바 있다. 그러나 충돌력의 영향이 약해지는 X/X₀=1.5 이후부터는 해석값과 실험값은 그 편차가 점차 줄어들어 서로 일치하는 분포를 보이고 있다.

Fig. 12

Turbulent kinetic energy (k) profiles developed in the X-Y plane

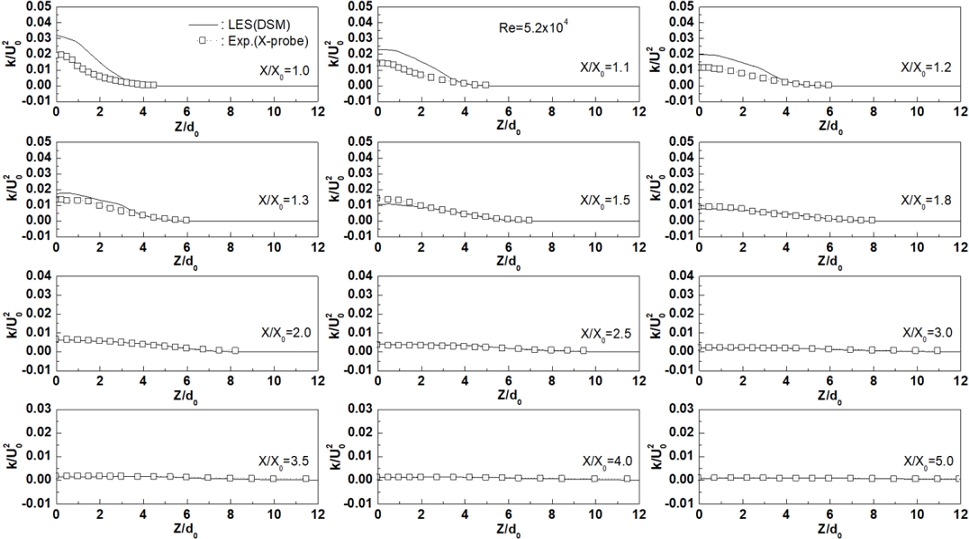
Fig. 13은 X-Z평면의 각 X축 방향의 위치에 따라 LES(DSM)로 해석한 난류운동에너지를 Z축 방향의 거리에 따라 나타낸 그림이다. X-Z평면의 1.0≤X/X₀≤1.3 영역에서 해석된 난류운동에너지도 실험값보다 크게 예측하나, X/X₀=1.5 이후부터는 그 편차가 크게 줄어들어 서로 일치한 분포를 보이고 있다.

Fig. 13

Turbulent kinetic energy (k) profiles developed in the X-Z plane

4. 결 론

두 원형분류를 수평으로 상호 45° 충돌시켰을 때 형성된 충돌분류의 LES 해석값과 실험값을 비교 분석한 결과는 다음과 같다.

1) 유동 반폭의 분포는 충돌력의 영향이 강하게 나타나는 1.0≤X/X₀≤2.0의 영역에서는 LES의 DSM과 WALE이 절댓값 기준 최대 약 25% 이내 오차율의 예측 성능을 보여 주며, X/X₀>2.0 이후에서는 DSM이 절댓값 기준 최대 약 6.5% 이내 오차율로 실험값과 잘 일치한다.

2) X축 방향의 평균속도 성분은 Y축 및 Z축 방향의 거리 증가에 따라 LES의 DSM으로 해석한 값은 충돌력이 강하게 지배하는 1.0≤X/X₀≤2.0에서 실험값보다 약간 작게 예측하는 것을 제외하면 대부분 서로 잘 일치한다.

3) X-Y평면 및 X-Z평면에서 LES의 DSM으로 해석한 난류운동에너지는 충돌력이 강하게 지배하는 1.0≤X/X₀≤2.0에서는 실험값보다 훨씬 큰 크기를 예측하지만, 그렇지 않을 때는 서로 잘 일치한다.

4) 난류운동에너지는 충돌점 근처에서 가장 큰 크기로 발달한다.

5) 두 원형분류를 45°로 충돌시켰을 때 형성된 충돌분류를 완벽하게 LES 모델로 해석하기에는 여전히 부족하나, 그 분포 경향을 모사하기에는 충분하다고 판단된다.

― 기 호 설 명 ―


b₁ :	Y방향의 유동 반폭 [mm]
b₂ :	Z방향의 유동 반폭 [mm]
d_i :	노즐 입구 직경 [mm]
d_o :	노즐 출구 직경 [mm]
cp :	두 노즐의 기하학적 충돌 점
k :	난류운동에너지 [m²/s²] {k=(u²+v²+w²)/2}
O :	충돌분류의 원점
Re :	레이놀즈수(Reynolds number)
X_o :	충돌 점까지의 축방향 거리 [mm]
U_o :	노즐 출구 속도 [m/s]
U :	X축 방향 평균속도 성분 [m/s]
u,v, w :	X, Y, Z축방향 변동속도 성분 [m/s]
X,Y, Z :	직교좌표계 좌표 및 거리 [mm]

Author contributions

J. K. Kim; Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Project administration, Supervision, Validation, Visualization, Writing-original draft, Writing-review & editing, Methodology, Software, Resources.

References

B. J. Rho and J. K. Kim, 1984, “An Experimental Study on the Turbulent Flow of a 45° Free Cross Jet”, Transactions of the Korean Society of Mechanical Engineers, 8(5), 442-449.
B. J. Rho and J. K. Kim, 1986, “Study on the Statistical Turbulent Characteristics of a 45° Circular Cross Jet Flow”, Transactions of the Korean Society of Mechanical Engineers, 10(1), 110-120.
B. J. Rho and J. K. Kim, 1987, “A Comparative Study on the Round Jet and the 45° Cross Jet”, Journal of the Korean Society for Aeronautical and Space Sciences, 15(1), 23-34.
B. J. Rho, J. K. Kim and H. A. Dwyer, 1990, “Experimental Study of a Cross Jet”, AIAA Journal, 28(5), 784-789.
J. K. Kim and S. H. Oh, 2011, “Numerical Analysis on the Turbulent Mixing Flow Field of 45° Impinging Round Jet”, Journal of the Korean Society for Power System Engineering, 15(3), 38-45.
J. K. Kim and S. H. Oh, 2009, “Evaluation of Turbulent Models on the Mixing Flow Structure of 45° Impinging Jet by Two Round Jets”, Journal of the Korean Society for Power System Engineering, 13(5), 34-39.
W. P. Jones and M. Wille, 1996, “Large-Eddy Simulation of a Plane Jet in a Cross-Flow”, International Journal of Heat and Fluid Flow, 17(3), 298-306. [https://doi.org/10.1016/0142-727X(96)00045-8]
P. Majander and T. Siikonen, 2006, “Large-Eddy Simulation of a Round Jet in a Cross-Flow”, International Journal of Heat and Fluid Flow, 27, 402-415. [https://doi.org/10.1016/j.ijheatfluidflow.2006.01.004]
B. Wegner, Y. Huai and A. Sadiki, 2004, “Comparative Study of Turbulent Mixing in Jet in Cross-Flow Configurations Using LES”, International Journal of Heat and Fluid Flow, 25, 767-775. [https://doi.org/10.1016/j.ijheatfluidflow.2004.05.015]
M. Popovac and K. Hanjalic, 2007, “Large-Eddy Simulations of Flow over a Jet-Impinged Wall-Mounted Cube in a Cross Stream”, International Journal of Heat and Fluid Flow, 28, 1360-1378. [https://doi.org/10.1016/j.ijheatfluidflow.2007.05.009]
SC/Tetra(Version 12), 2015, User's Guide, Software Cradle Co., Ltd.