기계 학습을 이용한 ORC용 터빈 형상 최적화
초록
본 연구에서는 선박에서 나오는 폐열을 이용하여 발전하는 ORC 시스템용 원심 터빈의 최적화를 다루고자 한다. 전통적인 방법을 통한 최적화는 시간과 비용이 매우 많이 들어간다. 이 문제를 해결하고자 실험계획법, 기계 학습, 그리고 Latin hypercube sampling을 이용하여 상대적으로 간단한 방법으로 최적화를 수행하였다. 구체적으로는 실험계획법 기반으로 다양한 조건에서 터빈형상을 변화시키고, CFD를 수행하여 얻은 결과를 통해 기계학습 모델을 만들어 최적화를 수행하는 기법이다. 위의 기법을 통해 설계점에서 최적화 전 터빈의 전효율 보다 1.3%p 이상 높은 성능을 가지는 터빈 형상을 얻을 수 있었다.
Abstract
In this study, our primary objective is to optimize a turbine employed in an Organic Rankine Cycle (ORC) system that harnesses waste heat from a ship. Traditional optimization methods are known to be time-consuming and expensive. To streamline a more practical optimization approach, we have leveraged design of experiment, machine learning, and Latin hypercube sampling. Our experimental design involves varying turbine geometries under different conditions and subsequently creating a machine learning model using the results derived from computational fluid dynamics simulations. Through the utilization of these methodologies, we have succeeded in achieving a turbine that surpasses the turbine isentropic efficiency obtained at the initial design point by 1.3% point.
Keywords:
Machine Learning, Organic Rankine Cycle, Radial Turbine, Optimization키워드:
기계 학습, 유기 랭킨 사이클, 터빈, 최적화1. 서 론
최근 컴퓨터의 연산 능력과 인공지능의 발달로 많은 분야로 인공지능 적용이 확대되고 있다. 기존 전문가의 경험에 의존하여 주로 이루어지던 터빈의 공기역학적 최적화를 위해서 인공신경망(Artificial Neural Network), 군집 최적화(Particle swarm method), 유전알고리즘(Genetic algorithm)과 통계적인 방법인 반응면기법(Response surface method) 등이 사용되고 있다.
인공신경망 모델은 1980년대부터 다항식으로 표현할 수 없는 함수에 적용할 수 있는 장점을 기반으로 널리 사용되기 시작했다. 초기에는 주로 유지보수를 위한 진단에 사용되었다. 그 이후 비정상 상태의 공기역학 제어에도 효과가 있음이 밝혀졌다. Greenman의 연구1)에 따르면, 높은 양력을 갖는 익형(airfoil)의 최적화에 신경망 기법이 사용되었고, 최적화에 사용되는 자원을 전통적인 구배 기반 최적화 대비 44% 감소시킬 수 있었다고 보고한다. Rai and Madavan2)은 터보 기계의 익형 설계에 신경망 기법은 추정과 예측에 효과적임을 밝혔다. 또 반응면 기법과 신경망 기법을 합성하여 적용하면 고차원의 문제를 다루는데 이점이 있음을 보고했다. 역전파 인공신경망(BPNN, Back Propagation Neural Network)이 제안되고 나서부터는 항력, 양력 계수 등의 예측에 더 효과적임이 보고되었다.3) 그러나 BPNN은 때때로 속도가 느렸고, 특정 문제에서는 다른 신경망 기법이 더 효율적이다. 그 이유는 각 단계에서 오차가 전 단계로 퍼져나갔기 때문이다. BPNN은 가장 많이 사용된 최적화 기법이지만 이러한 단점을 보완하기 위해 RBNN(Radial Basis Neural Network)이 제안되었다. RBNN 모델은 선형회귀를 이용하여 수학적으로 간단하므로 계산시간이 상대적으로 짧다. 비선형 결과가 요구될 때 정확도가 높고 적용성이 넓은 것으로 알려져 있다. BPNN과 비교하면, 많은 양의 학습 데이터를 이용할 수 있는 경우에는 BPNN보다 효율적이다.4,5)
최근에는 다중목적함수 최적화 또는 최적화 기법들을 복합 사용하는 연구가 보고되고 있다. Samad, A. 등6)은 다양한 대리 모델(PBA, RBNN, RSA, KRG)을 이용한 다중 목적함수를 갖는 압축기 최적화 연구를 수행했다. 대리모델을 조합함으로써 최적화의 강건성을 확보할 수 있음을 보고하였다. 대리모델의 조합을 위해서 일반적으로 회귀(regression) 예측력을 평가하는 통계적인 방법인 PBA(PRESS-Based-Averaging) 기법을 사용한다. 구체적으로는 PBA를 통해 정확도가 높은 모델에 높은 가중치를 부여하는 방식으로 대리모델 조합이 이루어진다. 유사한 방법으로 캐비테이션 모델에 대해 전역감도 해석을 통한 평가한 연구도 보고되었다.7) Pierret, S., & Van8)은 SA(Simulated Annealing)와 대리모델 개발을 통해 최적 형상을 도출하고 CFD를 이용하여 성능을 검증하였다. 목적 함수를 개발함으로써 기계적인 조건과 공력 조건을 모두 충족시킬 수 있음을 보고하고, 최적화의 완전 자동화가 가능함을 보였다. Shyy, W. 등9)은 반응면기법과 인공신경망을 이용하여 인젝터, 초음속 터빈, 디퓨저 등과 같은 로켓 추진 부품을 최적화에 대해 보고하였다. 이에 따르면, 전역적인 최적화는 다중 설계점과 균형(trade-off)을 다룰 수 있고, 다중 기준(multi-criterion) 최적화를 제공하며, 수치해석과 실험으로부터 발생하는 노이즈 필터링이 가능하다. 특히, 수치 계산, 실험, 이론 계산의 결과가 합쳐져야 할 때 반응면을 사용하든 신경망을 사용하든 모두 효과적임을 밝혔다. 이뿐만 아니라 연소실 압력 예측,10) 비파괴 검사를 위한 음향 방출 신호11)에 기계 학습을 활용한 연구가 보고 되었다.
본 연구에서는 선박에서 버려지는 열을 회수하여 발전하는 ORC 시스템용 터빈의 최적화를 수행하였다. 전문가의 경험에 의존하는 전통적인 방식을 개선하고자 기계 학습을 이용한 상대적으로 간소화된 터빈 형상의 최적화 및 기법의 유효성 확인을 목표로 한다. 작동 유체는 R1233zd(E)를 적용하였다. 100 kW급 출력을 얻기 위해서 회전 속도 25,500 rpm, 입구 온도 155℃, 입구 압력 2,106 kPa, 출구 압력 234.6 kPa의 조건 (팽창비 약 9)에서 작동하는 2단 원심 터빈이 등판 배치 형상(back-to-back layout)으로 개발되었다(Table 1). 본 연구에서는 기법의 유효성 확인을 위해 1단 터빈에 대해서만 최적화 과정을 다룬다. 최적 성능을 확보하기 위하여 인공신경망(RBNN)과 실험계획법(DOE, Design Of Experiment), 그리고 Latin Hypercube Sampling(LHS)이 함께 적용되었다.
2. ORC 터빈 설계
2.1 ORC 터빈 설계점
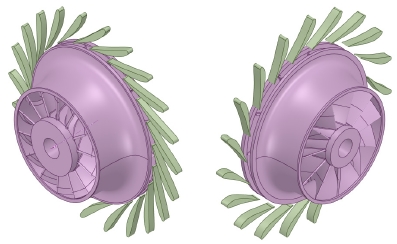
본 연구에서는 선박 폐열을 이용한 출력 100 kW급 ORC 터빈의 설계를 목표로 하고 있다. 작동 유체는 자연환경의 영향을 고려하면서 높은 효율을 확보하기 위하여 R1233zd(E)가 선정되었다. R1233zd(E)는 R245fa와 비슷한 시스템 효율을 가지고 지구온난화지수(GWP)가 매우 낮고 A1(ASHRAE) 안전 등급의 냉매이다. 팽창비 약 9인 시스템에서 높은 효율을 확보하고 축 방향 힘을 상쇄하기 위하여 등판 배치 형상을 가진 2단 원심 터빈 형상이 선택되었다(Fig. 1).
2개의 터빈은 1개의 축에서 등판 배치 구조로 되어 있어서 두 터빈의 회전 방향은 반대로 구성되어 있다. 본 연구의 목표인 최적화 설계와 비교를 위하여 설계점에서 성능을 얻기 위해 수치해석이 수행되었다. 최적화 방법은 동일하므로 1단 터빈을 분리하여 해석 및 최적화가 진행되었다.
수치해석 시 사용된 난류 모델은 SST 모델이다. 계산 영역은 4개로 구성되면 입구, 노즐, 로터, 출구 영역으로 구성되어 있으며, 회전 방향으로의 경계 조건은 주기조건을 주었다. 노즐과 로터가 연결되는 부분은 Mixing-stage(Constant total pressure)로 경계 조건을 처리하였다. 입구는 전압력 조건과 출구는 정압력 조건으로 주었다. 터빈은 팁 간극 손실(tip clearance loss)을 최소화하기 위해서 쉬라우드면이 있는 형상으로 설계되었다. 따라서 해석조건에서는 팁 간극을 0으로 주는 방식으로 처리되었다. 작동 유체 R1233zd(E)의 물성치는 단상의 기체로서 Peng & Robinson 상태방정식을 사용하였다. 격자수에 대해서는 1단 터빈에 50만 개 수준으로 적용하였다. 최적화의 목적함수로 사용할 등엔트로피 전효율(Isentropic total-to-total efficiency)을 기준으로, 최적화 전 수치해석 결과 설계점에서 91.1% 효율을 얻었다.
2.2 터빈 설계 변수 조정
폐열을 활용하는 ORC 시스템의 특성상 비용 회수 기간 최소화와 같은 경제성 확보를 위해 터빈의 효율을 높이고자 하는 요구가 많다. 터빈의 효율을 향상하기 위해서 형상의 최적화가 필요하다. 터빈 형상을 조절하는 방법은 매우 다양하므로, 최소의 설정값 변화를 통해서 조절할 수 있는 적절한 변수를 선택하여야 한다.
본 연구에서는 Cho. et al.12)의 방법을 적용하여 베지어(Bezier) 곡선으로 터빈의 형상을 표현하는 방법을 사용하였다. 이 경우에는 적은 수의 베지어 곡선의 조정점을 이용하여 터빈의 형상을 변경하는 것이 가능하고, 베지어 곡선의 조정점을 설계 변수로 선택하는 것이 가능해진다. 따라서 적은 수의 조정점으로 로터의 복잡한 형상을 변경하고 표현하는 것이 가능해진다.
본 연구에서는 로터의 허브면과 쉬라우드면에서 자오면 형상과 익형의 각도만 변화를 주면서 최적화를 진행하였다. 따라서 가능한 변수의 수를 적게 유지하기 위하여 로터에서 로터당 베지어 조정점 7개(로터 곡면 2개, 로터 각도 5개)를 사용하였다. Table 2, 3은 로터의 설계점에서 베지어 조정점과 제한 조건 값을 보여 준다. Table 2, 3에서 별도 표기(*)한 값은 최초 형상의 값이다.
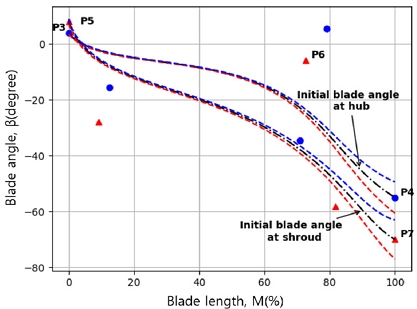
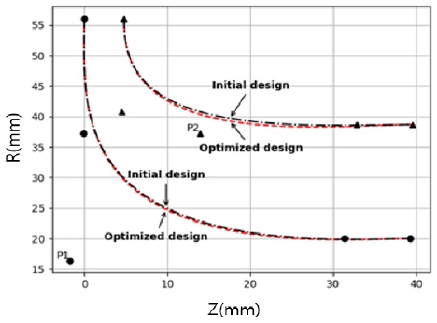
로터 형상에서 설계 변수로 선택된 조정점은 Z방향(축방향), R방향(반경 방향)으로 이동이 가능하나, 본 연구에서는 R방향(16.4 ± Ф1, 8.22 ± Ф2)만 조정하도록 설정되었다. Fig. 2, 3은 1단 로터의 허브와 쉬라우드에서 최초 설계값과 베지어 조정점을 움직였을 때의 로터 형상과 익형각의 변화하는 모습을 보여 주고 있다.
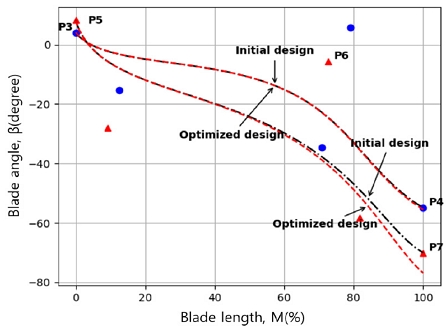
로터 각을 결정하는 베지어 조정점 5개 중에 쉬라우드 부분에서는 3개가 허브 부분에서는 2개가 설계 변수로 선택되었다. 3차원 블레이드의 각을 표현하는 방법은 익형각(β)과 자오면에서 익형의 곡선 길이(M)를 사용하여 표현되었다. 익형 각도의 조정은 쉬라우드에서는 입구와 가운데, 그리고 출구에서의 조정점이 설계 변수(8.22 ± Ф5, 5.74 ± Ф6, 69.96 ± Ф7)로 선정되었다. 허브에서는 입구, 출구에서 조정점이 설계 변수(4.0 ± Ф3, 55.0 ± Ф4)로 선정되었다.
본 연구에서는 터빈 로터에 대하여 총 7개의 설계 변수가 선택되었다. 로터 형상이 공력 측면과 구조적으로 적절하게 최소한의 제한 조건으로 변화를 주었고, 설계 변수값과 제한 조건은 Table 2, Table 3에서 확인할 수 있다. 그리고 로터 익형 형상 변화는 Fig. 2에서, 각도의 변화는 Fig. 3에서 확인할 수 있다. 익형의 두께는 구조적 안정성에 변화를 주지 않기 위해서 설계점에서 주어진 두께와 동일하게 분포하도록 설정하였다.
2.3 설계 최적화 방법
ORC 시스템의 터빈 로터 최적화에서 목적함수로 사용하는 효율이나 출력은 설계점 변화에 대해서 선형적으로 변하지 않는다. 따라서 최적화를 위해서 전역적 방법을 이용하여 최적화를 수행하여야 한다. 전역적 방법을 이용하여 최적화하면서 시간을 단축하기 위하여 실험계획법, 기계학습 방식의 하나인 RBNN 방식, 그리고 최적의 결과를 도출하기 위하여 LHS 기법을 사용하였다.
터빈 로터 최적화에 적용할 기계 학습 모델의 학습에 필요한 자료를 확보하기 위하여 실험계획법을 적용하였다. 진행 순서는 다음과 같다. 최적화하고자 하는 터빈 형상 설계 변수에 대하여 MINITAB 프로그램이 제공하는 부분 요인 배치 (Fractional Factorial Design)를 이용하여 각각의 단별 터빈에서 얻어진 7개의 설계 변수를 조정하여 64개의 다른 형상 조건을 얻는다. 이렇게 얻어진 64개의 형상은 Table 2, 3의 제한 조건 내에서 값을 가지게 된다. 64개의 형상에 대하여 수치해석을 수행하고 목적함수인 등엔트로피 전효율을 계산한다. 수치해석을 통해서 얻은 64개의 효율 값을 이용하여 기계 학습 모델(RBNN)에 대한 입력값을 만들어 학습된 모델을 구현한다.
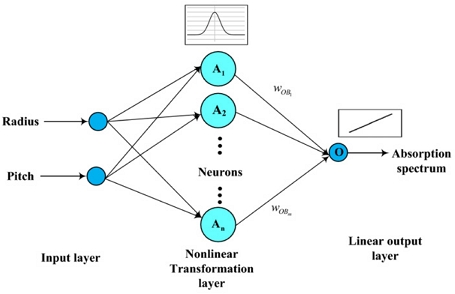
본 연구에서는 인공신경망 기법 중에 얇은 신경망 기법인 RBNN을 사용하여 대리모델 (Surrogate model)을 구축하였다. RBNN은 선형회귀에 근거하여 간단하고 속도가 빠른 최근에 개발된 다층 신경망이다. RBNN은 Fig. 4에서 보이는 것처럼 입력, 은닉, 출력층과 방사형 기저 함수와 선형 출력으로 구성되어 있다. RBNN을 사용하는 이유는 비선형 맵핑이 가능하고, 광범위한 적용성을 가지면서 내삽/외삽이 용이하기 때문이다. 단점으로 많은 데이터를 처리할 때 계산 비용이 증가하며, 다차원 회귀 구현할 때 내부 구조 설명이 어려울 수 있다. MATLAB 환경에서 RBNN을 식으로 구현하는 경우 출력층은 방정식(1)로 표현되며, w는 가중치 벡터이고, p는 입력값, b는 바이어스 값에 해당한다. 본 연구에서 RBNN은 MATLAB의 내장함수인 newrb 함수를 이용하여 구현되었고, 사용되는 기저 함수는 가우시안 함수이다.
| (1) |
| (2) |
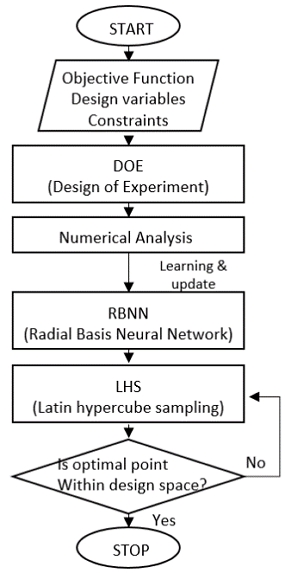
RBNN 모델을 이용하여 1단(spread constant = 10, error = 0.1)으로 설정하여 모델 학습을 구현한다. 학습 모델을 구현한 후, LHS 기법을 이용하여 다수의 설계점(설계 변수당 48,000)을 구한 후 학습된 RBNN 모델에 적용하여 최대 효율을 가지는 터빈 형상을 확보할 수 있다. LHS는 다양한 변수를 적용하고자 할 때 동일 간격으로 해당 범위 내의 값을 추출하는 방법이다. 최대 효율을 가지는 터빈의 형상이 설계 영역 안에서 확보되면 최적설계 과정이 종료되고, 확보되지 않는 경우 LHS의 설계점을 증가시켜서 다시 수행한다. 해당 과정은 Fig. 5에 순서도로 표시되어 있다.
2.4 결과 및 토의
터빈의 공력적 측면에서는 효율이 가장 중요한 특성을 고려하여 RBNN 모델의 목적 함숫값은 터빈의 등엔트로피 전효율로 설정하였다. 1단의 터빈에 대해서 실험계획법을 통하여 얻은 각각 64개의 터빈 효율 값을 이용하여 만든 모델에 LHS 기법을 통하여 최고 효율을 가지는 설계 조건을 찾아내었다. 본 연구에서는 MATLAB에서 제공하는 lhsdesign 함수를 이용하였다. RBNN을 이용해서 얻은 인공지능 모델에 설계 변수 조건식 내에서 설계값을 변화시키면서 최고의 효율을 얻는 조건을 찾는 것이 가능하다. RBNN 모델을 통해서 얻은 1단 터빈의 최적 설계값 5가지 경우가 Table 4에 주어져 있다. 해당 결과는 Fig. 6, 7의 P1~P7의 값과 효율로 나타냈다.
RBNN 방식으로 모델을 학습하는 과정에서 사용되는 설계 변수값과 목적 함숫값은 모두 정규화를 한 상태로 진행하여야 한다. 정규화하지 않는 경우, 절댓값 자체가 작은 설계 변수의 경우 변화의 영향을 제대로 나타내지 못하게 된다. 기존 설계값과 비교해 보면, 설계점에서 1단 터빈은 91.10%의 전효율을 가지고 있다. MATLAB에서 사용되는 RBNN 모델을 학습시키는 과정에서 기저 함수의 폭을 조절해서 최적의 값을 찾는 방식으로 작동한다. 모델을 학습시키는 과정에서 확산 상수(spread constant)가 사용되는데, 확산 상수는 각각의 층 속 뉴런(neuron)의 영향의 범위를 정의한다. 확산 상수를 조절해 가면서 결과를 검토하고, 최적 결과를 보여 주면 해당 상수를 모델의 값으로 선정한다. 앞에서 언급한 것과 같이 1단은 확산 상수(10)를 적용하였다. 이렇게 RBNN 모델을 이용하여 5회 반복하여 최적 효율(ηRBNN)을 얻은 결과는 92.78%을 얻었다. 이때 평균제곱오차는 0.347이다. 해당 결과는 비교의 기준이 되는 설계점의 효율(91.10%)보다 1.6%p 이상 높은 결과를 보여 주고 있다. 그러나 해당 결과는 RBNN 모델을 통한 결과이므로 검증이 요구된다. RBNN과 LHS를 통해서 확보된 설계 변수가 실제로 높은 효율을 가지는 것을 검증하기 위해서 최적 모델 Case 5의 설계 변수값에 대해 수치해석을 수행하였다. 수치해석은 처음에 RBNN 모델 교육을 위해 사용된 조건을 그대로 적용하였다. 이렇게 해서 얻어진 최적 효율(ηCFD)은 92.48%를 얻을 수 있었다. 최적화 전과 후의 형상은 Fig. 6과 Fig. 7에서 볼 수 있다. 터빈 쉬라우드 쪽의 R값이 줄어들고, 터빈 익형 각도는 허브 쪽은 거의 변화가 없고 쉬라우드 부분의 날개 끝단(trailing edge)에서 익형각이 증가하였다. 결론적으로 학습 모델에서 얻은 최적점의 수치해석 전효율 값이 최적화 전 설계점에서 수치해석을 통해서 얻은 전효율보다 1.3%p 이상 향상된 값을 보여 주고 있다.
다만 Table 4에서 보는 것처럼 효율 ηRBNN과 ηCFD를 비교해 보면, 모두 RBNN의 전효율 값이 수치해석의 결과보다 높게 나온다. RBNN이라는 인공지능 모델은 다른 관점으로 보면 학습에 사용된 다차원 데이터를 다차원으로 보간한 방정식으로 생각할 수가 있다. 이렇게 얻은 다차원 방정식에서 전역적으로 목적 함숫값을 최대가 되게 찾아내는 것이다. 그럼에도 불구하고 RBNN 모델은 블랙박스에 가까운 모델이기 때문에 수치해석 데이터를 입력 값으로 학습했지만, 수치해석보다 효율이 높게 나오는 이유를 추정하는 것에는 한계가 있다. 향후 연구에서는 이러한 이유를 추정하기 위한 연구를 수행할 필요가 있다.
3. 결 론
본 연구에서 선박에서 나오는 폐열을 회수하여 발전하는 ORC 시스템의 2단의 원심 터빈 중 1단 터빈 로터를 최적화하는 연구를 수행하였다. 터빈의 다른 부품(하우징, 씰, 디퓨저 등)의 변경을 최소화하기 위해 로터의 쉬라우드 및 허브 형상과 익형의 각도만 변경하여 최적 효율을 얻고자 하였다.
최적화 기법의 유효성과 성능을 확인하는 것을 목표로 하여 1단 터빈 로터 형상에 대해서만 실험계획법, RBNN 모델과 LHS 기법을 혼합한 방식으로 최적 설계값을 얻어내었다. 이렇게 얻어진 대리모델에 의한 최적 효율은 기존 형상의 수치해석 결과 기준 1.6%p 이상의 효율 증가를 확보했고, 검증을 위하여 해당 설계에 대하여 수치해석을 수행하였다. 이렇게 수치해석을 통해서 검증 및 최적화 전·후 결과를 비교했을 때, R1233zd(E)를 작동 유체로 하는 ORC 시스템에서 터빈 효율 기준 1.3%p 이상의 등엔트로피 전효율 향상을 확보하였다.
― 기 호 설 명 ―
| M : | Blade curve length |
| R : | Length at radial direction |
| Z : | Length at axial direction |
| T : | Temperature |
그리스 문자
| β : | Blade shape angle |
| Ф : | Deviation values for turbine rotor |
Acknowledgments
이 논문은 2023년도 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임(20220634, 선박 폐열을 활용한 발전 시스템 및 RCI 기술 실증).
Author contributions
J. Seo; Writing-original draft, Gi-won Byun; CFD analysis, Seon-ki Hong: CFD analysis, Ho-saeng Lee; Funding acquisition. S. Han; Writing-review & editing.
References
- R. M. Greenman, 1998, “2-D high-lift aerodynamic optimization using neural networks”, ASA TM-1998-112233. 146.
-
M. M. Rai, N. K. Madavan and F. W. Hubber, 2000, “Improving the unsteady aerodynamic performance of transonic turbines using neural networks”, 38th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, AIAA 2000-0169.
[https://doi.org/10.2514/6.2000-169]

- M. Norgaard, C. C. Jorgensen and J. C. Ross, 1997, “Neural network prediction of new aircraft design coefficients”, NASA TM-112197, 20.
-
R. Vaidyanathan, N. Papila, W. Shyy, P. K. Tucker, L. W. Griffin, R. T. Haftka and N. Fitz-coy, 2000, “Neural network and response surface methodology for rocket engine component optimization”, AIAA.
[https://doi.org/10.2514/6.2000-4880]

-
N. Papila, W. Shyy, N. Fitz-Coy, R. T. Haftka, 1999, “Assessment of neural net and polynomial-based techniques for aerodynamic applications”, 17th Applied Aerodynamics Conference, Norfolk, VA, AIAA 99-3167.
[https://doi.org/10.2514/6.1999-3167]

-
A. Samad, K. Y. Kim, T. Goel, R. T. Haftka and W. Shyy, 2008, “Multiple surrogate modeling for axial compressor blade shape optimization”, Journal of Propulsion and Power, 24(2).
[https://doi.org/10.2514/1.28999]

-
T. Goel, S. Thakur, R. T. Haftka, W. Shyy, and J. Zhao, 2008, “Surrogate model-based strategy for cryogenic cavitation model validation and sensitivity evaluation”, International journal for numerical methods in fluids, 58(9), 969-1007.
[https://doi.org/10.1002/fld.1779]

-
S. Pierret and R. A. Van den Braembussche, 1999, “Turbomachinery blade design using a Navier-Stokes solver and artificial neural network”, Journal of Turbomachinery, 121(2).
[https://doi.org/10.1115/1.2841318]

-
W. Shyy, N. Papila, R. Vaidyanathan and K. Tucker, 2001, “Global design optimization for aerodynamics and rocket propulsion components”, Progress in Aerospace Sciences, 37(1), 59-118.
[https://doi.org/10.1016/S0376-0421(01)00002-1]

-
Y. M. Kim, K. H. Seo, H. J. Choi, J. U. Lee and J. W. Lee, 2023, “Machine Learning-based Prediction of Combustion Chamber Pressure Using Crankshaft Angular Velocity”, Journal of Power System Engineering, 27(4), 36-46.
[https://doi.org/10.9726/kspse.2023.27.4.036]

-
J. J. Lee, D. Y. Cheong, D. H. Park and B. K. Choi, 2023, “Burst Signal Extract and Features Analysis for using Acoustic Emission in Machine Learning”, Journal of Power System Engineering, 27(1), 49-57.
[https://doi.org/10.9726/kspse.2023.27.1.049]

-
S. Y. Cho, Y. D. Lee, K. Y. Ahn and Y. C. Kim, 2013, “A Study on the Design Method to Optimize an Impeller of Centrifugal Compressor”, Korean Society for Fluid Machinery, 16(1), 11-16.
[https://doi.org/10.5293/kfma.2013.16.1.011]