The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 27, No. 6, pp.53-58

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 31 Dec 2023

Received 19 Oct 2023 Revised 12 Dec 2023 Accepted 12 Dec 2023

DOI: https://doi.org/10.9726/kspse.2023.27.6.053

배관 대칭 반사모드의 반사계수 특성 규명

박경조^*^{, †}

*교수, 전남대학교 기계설계공학부

Identification of Reflection Coefficients for Axi-symmetric Reflection Modes in Pipes

Kyung-Jo Park^*^{, †}

*Professor, Department of Mechanical Design Engineering, Chonnam National University.

Correspondence to: ^†Kyung-Jo Park : Professor, Department of Mechanical Design Engineering, Chonnam National University. E-mail : kjpark40@jnu.ac.kr, Tel : 061-659-7221

초록

이 논문에서는 배관에 축방향 모드가 입사되었을 때 결함에서 반사된 신호 중 축대칭 모드의 모드변환 특성을 실험적으로 규명하고자 한다. 선행 논문의 수치해석에 사용된 동일 배관에 대해 실험을 수행하여 축대칭 모드변환의 시간-주파수 특성을 분석하고 결함 크기와 반사계수 사이의 상관관계를 규명한다. 실험은 자왜센서를 이용한 비틀림 유도파를 배관에 가진하고 동일 센서로 결함반사 신호를 수신하는 방식을 사용하였다. 실험 결과로부터 원주방향 길이가 일정할 때 주 모드의 반사계수는 반경방향 깊이가 깊어지면 비례하여 선형적으로 증가하지만, 모드 변환된 모드는 반 정현파 특성을 보이며 두께의 절반 깊이에서 최대 반사계수를 갖는다는 것을 규명하였다.

Abstract

In this study, the characteristics of the axisymmetric modes from the defects are experimentally identified. The conclusions obtained by numerical simulation are experimentally verified using guided wave data from practical pipeline. The time-frequency features are identified and the relationship between defect size and reflection coefficient are investigated. Torsional guided waves are excited on the pipe using the magnetostrictive sensors and reflected signals from defects are detected using the same sensors. From the experimental results, it is verified that reflection coefficients of the mode-converted modes are appoximated to the shapes of the half-sine waves while the reflection coefficients of the principal modes is linear with respect to the extent of the defect.

Keywords:

Mode Conversion, Symmetric Mode, Chirplet Transform, Time-frequency, Reflection Coefficient

키워드:

모드변환, 대칭 모드, 첩릿변환, 시간-주파수, 반사계수

1. 서 론

선박구조물과 같은 평판이나 산업현장에서 널리 사용되는 배관의 결함을 검출하기 위해 유도파(guided wave)검사가 널리 사용되고 있으며, 관련 기술이 발전함에 따라 이전에는 검출하기 어려웠던 작은 결함도 찾아낼 수 있게 되었다.^1,2) 그러나 결함의 크기를 정량적으로 판단하는 것은 아직 많은 기술적 진보가 필요한데 그 이유는 반사 신호에 다중 모드가 섞여 있어 모드가 중첩되어 나타나기 때문이다.³⁾

반사계수(reflection coefficient)는 입사된 신호의 진폭에 대한 반사 신호의 진폭의 비로 정의되는데, 이를 이용하여 결함의 크기를 정량적으로 계산할 수 있다.⁴⁾ 따라서 지금까지 연구들은 대부분 결함에서 반사되는 비축대칭 모드에 초점을 맞추어 진행되어 왔지만 이 모드는 분산성이 크고 진폭이 작기 때문에 신호해석이 어려운 단점이 있다. 최근 축방향 모드를 입사하여 결함 반사신호를 측정하고, 이 중 모드 변환된 대칭 모드를 이용하여 결함의 크기를 정량적으로 규명하고자 하는 시도들이 있어 왔다.^5,6)

최근에 Park⁷⁾은 유한요소법을 이용하여 모드 변환된 신호의 반사계수를 구하고 이를 결함검출에 사용하여 비축대칭 모드를 이용할 때보다 정확한 정보를 얻을 수 있음을 보였다. 이 논문에서는 선행 연구의 유한요소해석에 사용된 동일 모델에 대해 실험을 수행하여 해석결과와 비교하고, 이를 통해 축대칭 반사모드를 이용하여 결함 크기를 정량적으로 규명할 수 있음을 보인다.

이를 위해 먼저 유한요소법을 이용한 모드해석에 대해 설명하고, 첩릿 변환(chirplet transform)을 이용하여 실험에서 구한 결함 반사 신호를 모드분리하고, 분리된 모드들의 반사계수를 계산하여 결함의 크기와 반사계수 사이의 상관관계를 규명한다. 그리고 결함의 종류와 크기에 따라 축대칭 반사모드의 반사계수가 변하는 양상을 규명하고자 한다.

2. 축대칭 모드변환 해석

선행 연구⁷⁾에서 유한요소법을 이용한 배관의 3차원 해석을 통해 배관에서의 파동전파 현상과 결함에서의 반사, 특히 모드변환이 발생하는 현상을 규명하였다. 해석은 강관의 모드형상 해석 및 축대칭 모드의 추출에 대해 수행하였고, 배관의 길이와 내경, 외경 그리고 결함의 위치 및 크기는 Fig. 1에 보인 바와 같다. 이 논문에서는 동일한 모델을 이용하여 해석을 수행하고, 그 결과를 실험 결과와 비교하고자 한다.

Fig. 1

Schematic diagram of the pipe with defect

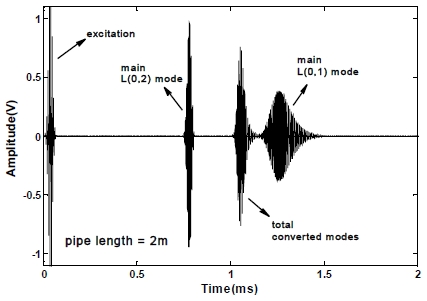
전체 배관 길이는 2 m, 내경과 외경은 각각 26, 34 mm이며, 두께는 4 mm이다. 결함은 배관의 중앙에 위치하고 있으며, 반경방향 깊이는 2 mm, 축방향 길이는 5 mm, 원주방향은 120°만큼의 크기를 갖도록 하였다. 이때 나타나는 결함반사 신호를 Fig. 2에 나타내었다. 신호는 세 개의 파동으로 구성되어 있는데, 각각은 주 L(0,2) 모드, 모드 변환된 종축방향 모드 그리고 주 L(0,1) 모드의 순서로 측정위치에 도달한다는 것을 알 수 있다.

Fig. 2

Reflection signals from defects

모드 변환된 신호에서 L(0,1), L(0,2) 모드를 분리하기 위해 첩릿 변환을 이용한 모드추출법을 사용하였다.⁸⁾ 첩릿 변환은 STFT 기법과 웨이브렛 변환의 장점을 모두 채택한 방법으로, 천이(시간과 주파수)와 확대, 전단(시간과 주파수) 기법을 적용하여 신호를 변환한다. Fig. 2에 제시된 반사 신호에 대해 첩릿 변환을 적용하면 L(0,2)모드에 의해 L(0,1)모드로 변환된 신호와 L(0,1)모드에 의해 L(0,2)모드로 변환된 신호를 분리할 수 있다.

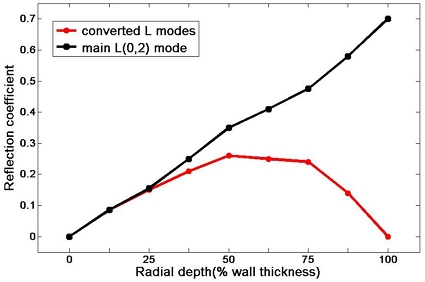
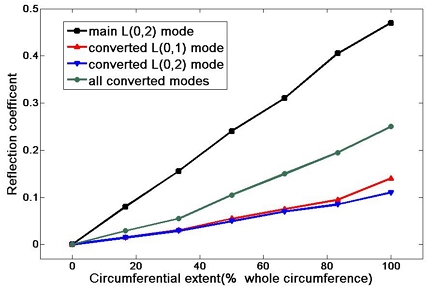
원주방향 길이를 전체 원주의 100% 즉, 360°로 가공하고 반경방향 깊이를 변화시켰을 때 나타나는 반사계수를 Fig. 3에 제시하였다. 그림에는 주 L(0,2)모드와 모드 변환된 L모드의 반사계수를 나타내었다. 주 L(0,2)모드의 반사계수는 반경방향 깊이가 증가할수록 선형적으로 비례하여 증가하는 반면, 모드 변환된 모드들의 반사계수는 반 정현파 형태를 갖는다는 것을 알 수 있다. 이는 반경방향 깊이를 일정하게 설정하고 원주방향 길이를 증가시켰을 때 나타나는 휨 파(flexural mode)의 반사계수 특성과 유사하다. 이러한 특성으로부터 모드 변환된 종파 모드는 결함의 반경방향 깊이에 민감하다는 것을 알 수 있다. 반경방향 깊이를 3 mm로 고정하고 원주방향 길이를 변화시켰을 때 나타나는 반사계수 특성을 Fig. 4에 제시하였다. 그림에서 주 모드나 모드 변환된 모드들 모두 반사계수가 원주방향 크기에 선형적으로 비례하여 증가하는 것을 알 수 있다.

Fig. 3

Reflection coefficient at whole circumference

Fig. 4

Reflection coefficient at 3 mm radial depth

3. 실험장치 및 결과

유한요소법을 이용하여 규명한 종방향 모드의 축대칭 모드 변환 특성을 확인하기 위해 실제 배관을 이용한 실험을 수행하였다.

실험에 사용된 배관은 수치해석에 사용된 배관과 동일한 재질인 탄소강으로 이루어져 있으며 길이는 2 m이다. 결함은 노치 형태로 가공하였으며 배관 끝단에서 1 m 떨어진 곳에 위치한다. 결함의 반경방향 깊이는 네 가지 경우(1 mm, 2 mm, 3 mm, 4 mm)를 고려하였으며, 원주방향 길이는 전체 원주의 1/3(120°), 2/3(240°), 3/3(360°) 세 가지 경우로 가공하였다.

결함의 축방향 길이는 10 mm로 고정하였다. 반경방향과 원주방향 결함 길이는 세 가지 조합으로 구성하였다. 첫 번째는 원주방향으로는 360° 길이(축대칭 결함)를 유지하면서 반경방향으로 깊이가 달라지는 경우, 두 번째는 반경방향으로는 1 mm 깊이(두께의 25%)를 유지하면서 원주방향의 길이를 변화시키는 경우 그리고 마지막으로 반경방향으로 3 mm 깊이(두께의 75%)를 유지하면서 원주방향 길이를 변화시키는 경우로 구성하였다.

실험 장치는 Fig. 5와 같이 파형발생기, 파워 증폭기, PZT센서, 신호수신기 그리고 고속 데이터취득 장치로 구성하였다. L(0,2)모드를 기진하기 위해 배관의 한쪽 끝단에 해닝 윈도우를 씌운 5사이클 톤버스트(tone-burst) 신호를 인가하였다. 인가된 신호는 16개의 링으로 구성된 신호변환기(20×4×0.5 mm³⁾의 원주방향으로 균일하게 입사되어 L(0,2)모드와 L(0,1)모드를 동시에 가진한다.

Fig. 5

Experimental setups for guided waves test

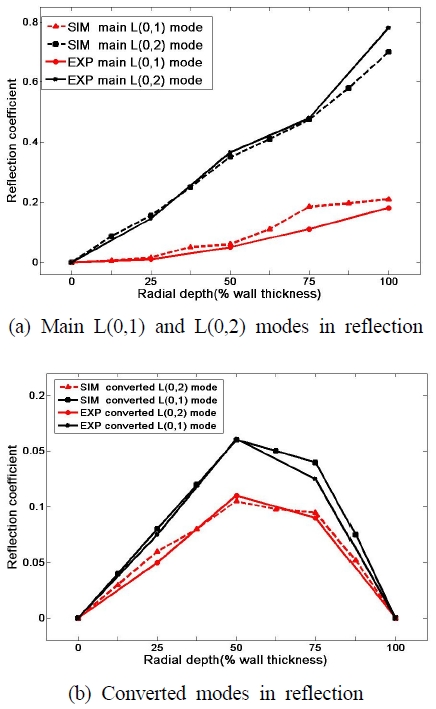
수신기에 수신된 신호 중 전형적인 신호를 Fig. 6에 나타내었다. 신호가 측정되는 순서는 선행 연구에서 예측한 대로 반사된 L(0,2)모드, 모드 변환된 모드 그리고 반사된 L(0,1)모드 순으로 측정 된다.⁹⁾ 실험결과에 영향을 미치는 인자는 배관의 재료 특성, 가공오차, 신호에 섞이는 잡음 등 많은 요소들이 있기 때문에 수치해석 결과와 실험결과가 완벽하게 일치하지는 않는다. 첩릿변환에 기반 한 모드추출법 CTME(Chirplet Transform-based Mode Extraction)⁷⁾을 이용하여 모드 변환된 모드에서 L(0,1), L(0,2)모드를 분리한 결과를 Fig. 7, 8에 나타내었다. 실험 결과와 해석 결과가 비교적 잘 일치하는 것을 확인할 수 있다. 반경방향 깊이가 1 mm(전체 두께의 25%)일 때 실험 결과와 해석결과의 차이가 가장 크게 나타나는데, 이는 결함의 가공오차(결함 크기가 작을수록 가공오차가 커짐), 배관 두께의 불균일성 그리고 재료의 특성 등에 의한 것으로 파악된다.

Fig. 6

Reflection signals from experiments

Fig. 7

Comparison of reflection coefficient at whole circumference

Fig. 8

Experimental reflection coefficient when radial depth is 3 mm(3/4 thickness)

Fig. 7(a)에는 결함의 깊이가 반경방향으로 깊어질 때 실험에 의한 L(0,1), L(0,2)모드의 반사계수를 수치해석 결과와 비교하여 나타내었다. Fig. 7(b)는 모드 변환된 모드에 대한 결과이다. 모드 변환되지 않은 모드는 L(0,1), L(0,2)모드 모두 결함의 깊이가 깊어질수록 반사계수도 선형적으로 증가하는 것을 볼 수 있다. 반면 모드 변환된 모드들은 반 정현파 형태로 반사계수의 크기가 나타나는데, 결함 깊이가 두께의 1/2일 때 최고치를 갖는 것을 알 수 있다. 모드 변환된 L(0,1), L(0,2)모드 모두 동일한 특성을 가지며, 두 모드가 합쳐진 총 모드-변환 모드도 같은 특성을 보인다. 따라서 실제 실험에서는 모드분리를 통해 구한 단일 모드보다 총 모드를 사용하는 것이 효율적이라고 할 수 있다.

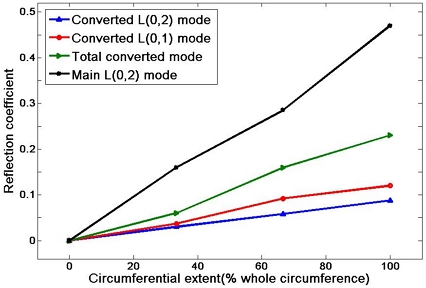
Fig. 8에는 결함의 깊이가 3 mm일 때 원주방향 길이의 변화에 따른 반사계수를 나타내었다. 그림에서 원주방향 길이가 커질수록 모든 모드의 반사계수도 선형적으로 증가하는 것을 알 수 있다.

또한 결함의 깊이가 깊을수록 주 모드와 모드 변환된 모드 사이의 반사계수 차이도 커지는 것을 알 수 있다. 이로부터 결함의 반경방향 깊이가 종축방향 대칭모드 반사의 반사계수에 가장 중요하게 영향을 미친다는 것을 알 수 있다.

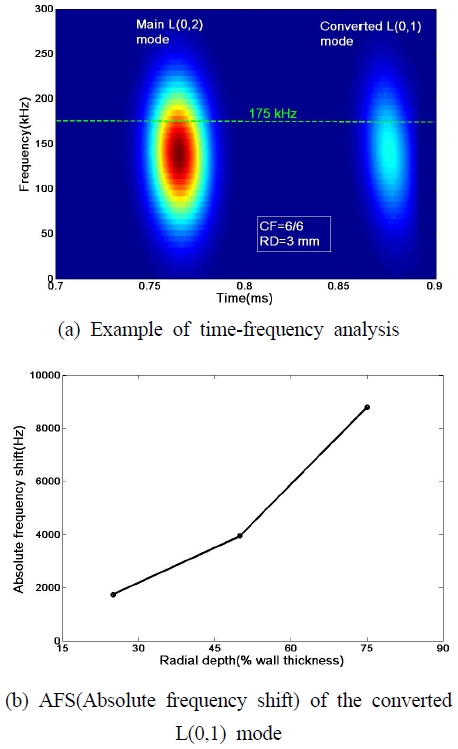
결함에서 반사된 신호의 각 모드들에서 나타나는 주파수 이동(frequency shift) 현상에 대해서도 조사하였다. 원주방향 길이를 고정(원주의 100%)하고 반경방향 깊이를 변화시켰을 때 측정한 반사 신호에 시간-주파수 해석을 수행하였고, 그 결과를 Fig. 9에 나타내었다. 그림에서 주 신호인 L(0,2)모드의 중심주파수가 아래쪽으로 이동한 것을 알 수 있다. 즉, 중심주파수가 175 kHz에서 145 kHz로 이동한 것을 확인할 수 있다. 모드 변환된 L(0,1)모드의 경우 반경방향 깊이를 증가시키면 절대주파수천이(absolute frequency shift)는 단순 증가하는 것을 Fig. 9(b)에서 알 수 있다. 즉 모드 변환된 모드의 주파수 특성은 결함의 반경방향 깊이에 민감하다는 것을 알 수 있다.

Fig. 9

Time-frequency analysis results and absolute frequency shift for experimental signals

4. 결 론

이 연구에서는 배관에 대칭 모드가 입사되었을 때 결함 반사 신호를 모드 분리하고, 분리된 신호 중 축방향 대칭 모드의 특성에 대해 기술하였다.이 연구에 대한 결론은 다음과 같이 정리할 수 있다.

1) 유한요소해석에 사용된 동일 모델에 대한 실험 결과로부터 모드 변환된 축대칭 반사 모드를 이용하여 결함의 크기를 정밀하게 규명할 수 있음을 알 수 있었다.

2) 실험 결과는 수치해석 결과와 유사한 특성을 나타내는 것을 확인하였다. 원주방향 길이가 일정할 때 주 모드의 반사계수는 반경방향 깊이가 깊어지면 비례하여 선형적으로 증가하지만, 모드 변환된 모드는 반 정현파 특성을 보이며 두께의 절반 깊이에서 최대 반사계수를 갖는다는 것을 규명하였다.

3) 반경방향 깊이가 일정하면 원주방향 크기가 증가할수록 주 모드, 모드 변환된 모드 모두 단순 증가하는 것도 확인하였다.

이로부터 결함검출에 모드 변환된 축대칭 모드를 활용하면 결함에 대한 보다 정확하고 다양한 정보를 얻을 수 있음을 입증하였다.

Author contribution

K. J. Park: Conceptualization, Methodology, Analysis, Experiment, Writing original draft and review, Editing.

References

A. Demma, P. Cawley, M. Lowe, A. G. Roosenbrand and B. Pavlakovic, 2004, “The reflection of guided waves from notches in pipes: a guide for interpreting corrosion measurements”, NDT&E International, 37(3), 167-180. [https://doi.org/10.1016/j.ndteint.2003.09.004]
R. Carandente and P. Cawley, 2012, “The effect of complex defect profiles on the reflection of the fundamental torsional mode in pipes”, NDT&E International, 46, 41-47. [https://doi.org/10.1016/j.ndteint.2011.11.003]
L. Satyarnarayan, J. Chandrasekaran, B. Maxfield and K. Balasubramaniam, 2008, “Circumferential higher order guided waves modes for the detection and sizing of cracks and pinholes in pipe support regions”, NDT&E International, 41(1), 41-47. [https://doi.org/10.1016/j.ndteint.2007.07.004]
D. N. Alleyne, B. N. Pavlakovic, M. J. S. Lowe and P. Cawley, 2001, “Rapid, long range inspection of chemical plant pipework using guided waves”, AIP Conference Proceedings, 20(1), 180-187. [https://doi.org/10.1063/1.1373757]
A. Shelke, U. Amjad and M. Vasiljevic et al., 2015, “Extracting quantitative information on pipe wall damage in absence of clear signals from defect”, J. of Pressure Vessel Technology, 134(5), 51-59. [https://doi.org/10.1115/1.4005877]
X. Wang, H. Gao, Kai Zhao and C. Wang, 2021, “Time- frequency characteristics of longitudinal modes in symmetric mode conversion for defect characterization in guided waves-based pipeline inspection”, NDT&E International, 122(4), 102490. [https://doi.org/10.1016/j.ndteint.2021.10.2490]
K. J. Park, 2022, “Characterization of axisymmetric reflection modes and detection of defect in pipelines”, Journal of Korean Society for Power System Engineering, 26(5), 30-37. [https://doi.org/10.9726/kspse.2022.26.5.030]
Y. W. Kim and K. J. Park, 2014, “Mode separation in torsional guided waves using chirplet transform”, Transactions of the Korean Society for Noises and Vibration Engineering, 24(4), 324-331.
Y. W. Kim and K. J. Park, 2014, “Mode separation in torsional guided waves using chirplet transform”, Transactions of the Korean Society for Noises and Vibration Engineering, 24(4), 324-331. [https://doi.org/10.5050/ksnve.2014.24.4.324]
C. Yeung and C. T. Ng, 2019, “Time-domain spectral finite element method for analysis of torsional guided waves scattering and mode conversion by cracks in pipes”, Mechanical Systems and Signal Processing, 128, 305-317. [https://doi.org/10.1016/j.ymssp.2019.04.013]