연속 접촉 헬리컬 기어펌프의 수치해석 연구: 모델 개발 및 적용

2.1 이중원호 연속접촉 기어 치형의 설계

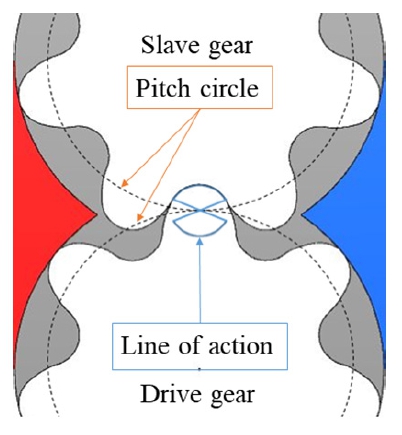
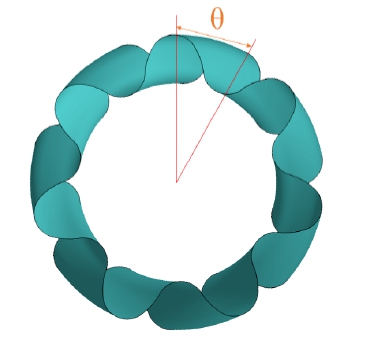
본 연구 대상인 연속 접촉 헬리컬 기어펌프의 치형은 원호와 인벌류트 곡선을 사용하여 기존 단순 인벌류트 기어 치형을 Fig. 1과 같이 인벌류트-원호 기어 치형으로 변경하여 폐입이 최소화 되도록 고안되었다.^3,7-8) Fig. 2에 나타낸 바와 같이, 기어는 원호와 맞물린 상태에서 인벌류트 곡선으로 전환되어 표시된 파란색 선을 따라 연속 접촉하므로 폐입이 거의 발생되지 않는다. 이를 바탕으로 원호와 수식화된 인벌류트 곡선을 접합하여 기어 치형 설계를 수행하였다.

Fig. 1

Profile of a tooth for the designed circular arc/involute gear profile

Fig. 2

Meshing lines of CCHGP

2.2 수치해석 펌프 모델

본 연구에 적용된 헬리컬 기어 펌프의 형상을 Fig. 3에 나타내었다. 펌프 케이싱 내에는 인벌류트-원호 치형으로 설계된 7개의 이를 갖는 동일한 기어가 위치하고 내경이 20.0 mm인 포트가 양 끝단에 연결되어 있는 구조로 설계되었다. Fig. 4에 나타낸 전체 헬리컬 회전 각도(total helical rotation angle)는 헬리컬 기어에서 동일한 이를 기준으로 앞면과 뒷면 사이의 회전 각도를 의미하며, 이는 식 (1)과 같이 계산된다.

Fig. 3

Extracted fluid volume of CCHGP, (a) entire fluid volume, (b) fluid volume of port2, (c) fluid volume in rotation, (d) fluid volume of port1

Fig. 4

Total helical rotation angle [θ]

여기서, H는 기어의 리드, N은 기어의 잇수, m_t는 축직각 모듈(transverse module), β는 헬릭스 각도를 각각 의미하고, 전체 헬리컬 회전 각도 θ는 피치 각도와 같으므로 θ=2π/N 이다.

펌프의 배제용적 dV는 다음과 같다.

여기서, f는 맞물림 지점과 피치 지점과의 거리이고, R_e는 팁의 반지름, R은 피치원 반지름이다.

단위각도당 배제용적은 식 (3)과 같다.

여기서, 헬리컬 면적 p=H/2π, m_n은 모듈이다. 기어의 폭 B는 다음과 같다.

식 (4)를 식 (3)에 대입하여 정리하면 단위각도당 배제용적은 다음과 같다.

그러므로 이론 체적유량은 다음과 같다.

본 연구에 사용된 펌프 주요 제원을 Table 1에 나타내었다. 기어의 외경 33.16 mm, 헬릭스 각도는 20.56 deg, 회전축 방향으로 기어의 높이는 35.4 mm로 설계하였다. 기하학적 치형으로부터 계산된 펌프의 배제용적은 17.93 cc/rev이다.

Table 1

Design parameters for CCHGP

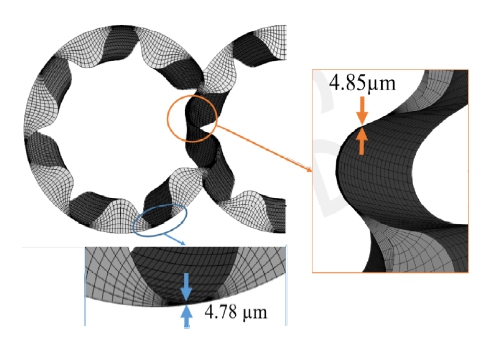
기어 백래시로 인한 기어 맞물림 부의 틈새는 4.85 μm, 기어와 케이싱의 틈새를 포함하여 운전 중 일정한 편심을 갖는 기어의 격자 형상을 Fig. 5에 나타내었다. 이러한 간극으로 인한 틈새를 통하여 내부 누설이 발생된다. 본 연구에서는 연속 접촉 인벌류트-원호 치형을 상용 해석 프로그램인 SimericsMP+의 기어 탬플릿에 적용하여 헬리컬 기어의 격자를 생성하였고 기어와 펌프 케이싱 및 양쪽 포트가 MGI(miss-matched grid interface)로 연결되어 시뮬레이션이 수행된다.^9,10)

Fig. 5

Meshing feature and clearance

2.3 격자 민감도 분석

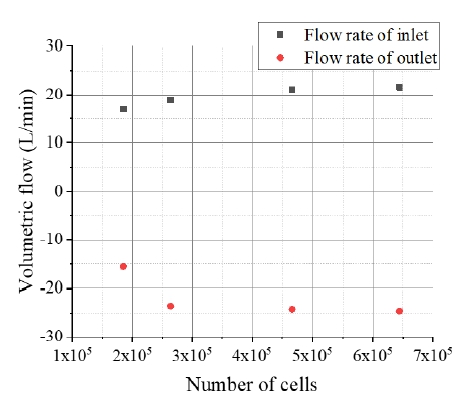
펌프 내부에 형성되는 복잡한 난류유동을 정밀하게 모사하기 위해서는 물리적으로 잘 정렬되어 적은 격자수를 갖는 모델을 선정하는 것이 바람직하다. 수치해석 계산시간 최소화 및 정밀도 확보를 위한 목적으로 격자 민감도 분석을 수행하였다. Fig. 6에 붉은 점과 파란 점은 각각 격자수에 따른 송출 및 흡입 평균 체적유량을 나타낸다. Fig. 6의 결과로부터 격자수가 증가함에 따라 유량이 수렴하는 것을 알 수 있다. 이를 통해 헬리컬 기어펌프의 격자 형성을 위해서는 기어 축 방향으로 최소 50개 이상의 레이어(layer)와 180,000개 이상의 격자가 필요함을 확인하였다. 그러므로 격자수가 180,000~650,000개인 4개의 모델을 대상으로 1,500 rpm, 토출 압력 200 bar의 조건으로 유동해석을 진행하였고, 600,000개 이상의 격자에서 유량이 일정한 값으로 수렴되었다. 따라서 본 논문에는 640,000개의 격자를 갖는 모델을 적용하여 시뮬레이션을 수행한다.

Fig. 6

Results of Mesh sensitivity for CCHGP

2.4 지배방정식과 유체영역의 정의

3차원 전산유체해석에 사용된 펌프의 유체영역을 Fig. 7에 나타냈다. 입출구 포트, 케이싱, 연속접촉 스퍼기어의 형상을 캐드로 구현하여 유체영역을 생성하였고, Table 2에 시뮬레이션에 사용된 경계값 및 유체 물성치를 정리하였다. 본 시뮬레이션에서는 압력 불평형에 의한 기어의 편심량은 일정한 것으로 가정한다. SimericsMP+를 사용하여 유체영역은 MGI로 연결하였고 k-ε 난류 모델과 캐비테이션 모델을 지배방정식으로 적용하여 수치해석이 수행된다.^3,9-10)

Fig. 7

Fluid domain and MGI

Table 2

Design parameters for boundary

또한 유체를 기체와 증기의 질량을 포함하는 다상 흐름의 균질한 혼합물로 가정하면 질량과 운동량 보존 방정식은 다음과 같이 적분 형식으로 표현된다.

여기서, Ω(t)는 시간에 따른 검사체적, σ는 검사체적의 검사면, n은 검사면의 법선 벡터, ρ는 유체의 밀도, f는 유체력, ν는 유체의 속도, ν_σ는 검사면의 속도, $$ \tilde{\tau }$$는 전단응력 텐서를 의미하고 식 (8)의 우변은 점성력과 압력을 각각 나타낸다.

Singhal et al. 등은 Navier-Stokes 방정식과 난류 모델을 이용하여 유체 밀도를 증기 질량분율 f_v의 함수로 정의하였고,¹⁰⁾ f_v는 식 (9)의 수송방정식으로 결정된다.

여기서, D_f는 증기의 확산률, μ_t는 난류 점성계수, σ_f는 난류 슈미트 수(Schmidt number)이다. R_e와 R_c는 증기 생성률과 증기 응축율을 각각 나타내며 식 (10)~(11)과 같이 나타낼 수 있다.

여기서, C_e와 C_c는 캐비테이션 증발계수와 응축계수를 각각 의미하며, g_f는 가스의 질량분율, ρ_l과 ρ_v는 각각 액체와 증기의 밀도이다.

한편, 국부 압력변화는 포화증기압에 따라 증기의 생성과 소멸을 유발하게 된다. 국부압력 변화가 어떤 임계값 이하가 되면 액상의 유체는 증기로 상변화가 일어나게 되고, 이 부분이 증기 질량분율 수송방정식의 생성항으로 표현된다. 수송방정식과 운동량 보존방정식으로부터 ρ-f와의 관계는 식 (12)와 같고, 증기 체적분율 α와 f과의 관계는 식 (13)으로 표현된다.

포화증기압은 온도에 관한 함수로 정의되며, 증발과 응축 계수는 일반적으로 사용하는 0.02와 0.01로 각각 설정하였다.

3.1 펌프 시뮬레이션

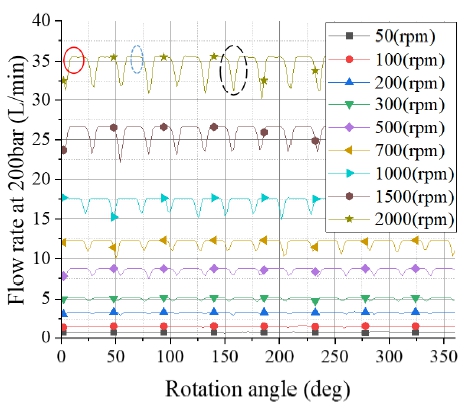
식 (5)를 이용하여 계산된 CCHGP의 배제용적은 17.93 cc/rev이고, 식 (6)을 이용하면 일정한 펌프 회전수에 대한 이론 유량이 계산된다. 200 bar의 일정한 출구 압력을 적용하여 기어 회전속도 변화에 따른 유량 맥동 시뮬레이션 결과를 Fig. 8에 나타내었다. Fig. 8에서 체적 유량의 순시치는 두 개의 기어가 맞물리는 치형 특성에 의한 내부 누설 유량의 변화와 유체 압축성의 영향으로 1회전당 14번의 주기로 반복되는 것을 확인할 수 있었다. Fig. 8에서 붉은원으로 나타낸 흡입 맥동 이후 약간의 유량 리플(빨간색 원, Fig 8)은 1,500 rpm 이하의 회전속도 모델에서는 관찰되지 않았다.

Fig. 8

Volumetric flow rate with rotation angle

이후 Fig 8에서 파란 사각 점선원으로 나타낸 유량 맥동이 거의 없는 구간에서는 누설을 제외하면 이론 유량 곡선과 양호하게 일치한다. 이는 인벌류트 치형의 일정한 기어 백래시에 의한 영향인 것으로 판단되므로, 백래시와 누설 유로 단면적의 변화는 크지 않음을 알 수 있다.

Fig 8에서 검은 긴 파선원으로 나타낸 유량 맥동은 회전수에 반비례하므로 주동 기어에 의해 반경방향으로 이송된 저압의 유체가 고압의 출구 포트와 만나게 되어 나타나는 일종의 유체 스프링 효과로 인해 발생되는 것으로 추정되고, 이는 유체의 압축성을 반영한 결과로 해석된다.

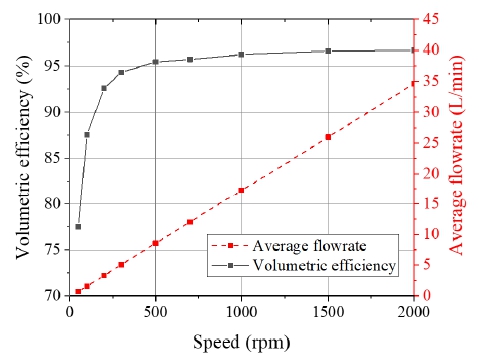
Fig. 9에 기어 회전속도에 따른 체적효율과 평균 체적유량을 나타내었다. 300~2,000 rpm 구간에서 체적효율은 94.3~96.7%로 비교적 높게 나타났으나 저속 구간인 200~50 rpm에서의 체적효율은 92.6~77.5%로 약간 감소하였다. 이는 본 연구에 사용된 펌프 모델은 케이싱 내 기어의 편심량의 변화가 없어, 회전속도가 변화하더라도 누설유량은 거의 동일하기 때문에 나타나는 현상으로 사료된다.

Fig. 9

Volumetric efficiency and average flow rate

선행 연구에서³⁾ 저속, 고압 조건보다 고속, 고압 조건에서 기어 회전축의 편심량이 약간 감소되는 경향이 있는 것으로 보고되었으나, 본 연구에서는 해석의 간편성을 위해 입구와 출구 포트의 압력이 일정하면 기어의 회전속도가 증가하여도 기어축의 편심과 축간 거리는 일정하다고 가정하였다. 따라서 기어의 백래시와 5.0 μm인 케이싱과의 틈새로 인한 내부 누설 유량은 거의 일정하며, 유체의 압축성이 반영되어 저압 포트에서 이송된 유체가 고압 포트와 연결됨에 따라 발생하는 비교적 소량의 유량 맥동만이 관찰된다. 그러나 실제 펌프에서는 입출구 차압과 회전속도 변화에 따라 틈새도 변하므로 편심량과 유체의 체적탄성계수를 고려한 연구가 추가적으로 필요하다고 판단된다.

3.2 압력 맥동

Fig. 7에 나타낸 관측 지점(monitoring point)에서의 회전속도별(300, 1000, 2000 rpm) 압력맥동을 Fig. 10에 나타낸다. 송출압력을 200 bar로 설정한 Fig. 10의 결과로부터 회전속도와 무관하게 27.5 도의 일정 주기로 반복되는 압력 맥동으로 인한 압력의 최대-최소치는 2,000 rpm의 고속구간에서 0.0017 bar 내외의 가장 큰 값으로 계산되었으므로 압력맥동의 크기는 대체로 회전속도에 비례하는 경향이 관찰되었다.

Fig. 10

Pressure variation with rotational angle

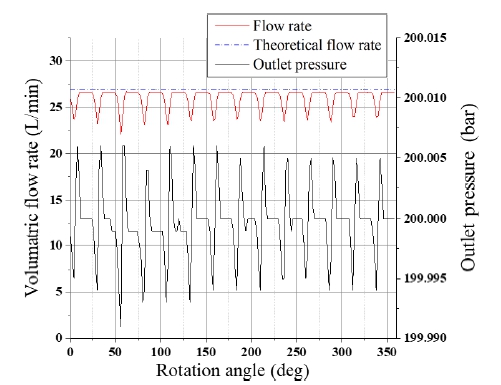
송출압력 200 bar, 회전속도 1,500 rpm에서 펌프의 이론 유량 및 시뮬레이션 유량과 압력맥동을 각각 Fig. 11에 나타낸다. Fig. 11의 결과로부터 출구포트로 이송된 유체가 압출된 직후 유량 맥동 및 압력맥동이 각각 관찰되고, 이후 압력과 유량이 안정화되는 현상이 27.5도의 일정 주기로 반복됨을 알 수 있다. 한편, 반영되지 않은 제작공차와 편심량을 추가적으로 고려한다면 실제 압력 맥동의 크기는 조금 더 감소될 것으로 예상된다.

Fig. 11

Pulsation of flow rate and pressure according to the angle of gear

3.3 캐비테이션의 예측

유체 본연의 압축성과 더불어 기어와 케이싱 사이의 반경 방향 틈새 및 기어 맞물림시의 백래시 등은 상대적으로 저압 상태인 흡입 포트 주변의 국부적인 지점에서의 압력에 큰 영향을 주게 되고 이는 CCHGP의 캐비테이션 발생에 가장 주요한 원인으로 작용할 것으로 판단된다.

본 연구에서는 전술한 캐비테이션 현상을 확인하기 위하여 캐비테이션 모델을 CCHGP의 수치해석 모델에 포함하여 시뮬레이션을 수행하였고, 그 결과를 Fig. 12와 13에 각각 나타낸다. Fig. 12에 CCHGP의 z평면상의 가스 체적분율에 대한 시뮬레이션 결과를 나타내었다. Fig. 12의 시뮬레이션 결과로부터 백래시 등으로 인한 기어 맞물림에서의 일정한 틈새를 통해 캐비테이션이 주로 발생하는 것으로 확인되었으며, 추가적으로 흡입 측에서의 기어와 케이싱 사이에서도 캐비테이션 발생이 관찰되었다.

Fig. 12

Gas volume fraction of cavitation

Fig. 13

Total Gas volume fraction of CCHGP

흡입 및 송출 포트를 제외하고 펌프 내부 유체영역에서 생성된 가스 체적분율을 Fig. 13에 각각나타내었다. 50 rpm에 비해 2,000 rpm에서 가스 체적분율이 약 2배 높게 나타나 펌프 회전수가 증가함에 따라 캐비테이션이 증가하는 것으로 나타났으나, 2,000 rpm의 회전속도에서 96%에 이르는 CCHGP의 높은 체적효율을 고려하면 발생된 캐비테이션이 CCHGP의 성능에 미치는 영향은 그다지 크지 않은 것으로 판단된다.

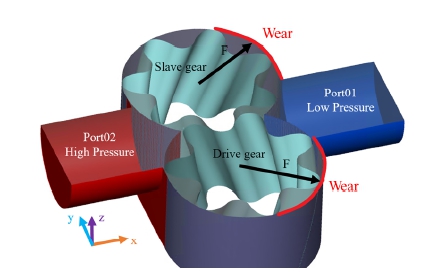
3.4 기어에 발생하는 힘과 축 추력

헬릭스 기어의 축 추력은 구동 토크에서 전달되는 추력과 헬릭스 각도를 따라 토출되는 유체 압력에 기인한 추력의 합력으로 계산된다. Fig. 14에 토출압력 200 bar, 회전속도 1,000 rpm의 운전영역에서 축(shaft)에 형성된 합력을 나타낸다. Fig. 15에 구동기어와 피동기어에 작용하는 x,y,z축 방향의 힘을 각각 나타낸다. 송출압력 200 bar인 경우에는 펌프의 축방향 추력(F_zd, F_zs)이 약 720 N으로 확인되었다. 이러한 추력은 펌프의 배제용적과 송출 압력에 비례하여 대체로 증가하므로 펌프 설계시에 축방향 추력이 펌프의 배제용적과 송출압력을 제한하는 요인으로 작용한다. 그러므로 송출압력에 따라 구동기어와 종동기어의 추력 불평형을 적절히 보상하기 위한 저널 베어링과 가동 측판 설계에 대한 연구가 추가적으로 필요할 것으로 사료된다.

Fig. 14

Total forces applied to the gear shaft by differential pressure at 200 bar and 1,000 rpm of operating condition

Fig. 15

Forces applied to the gear shaft

Author contributions

S. W. Ji; Conceptualization, Funding acquisition, Project adminstration, Methodology, Supervision, Validation, Writing-review & editing. H. S. Jang; Data curation, Formal analysis, Investigation, Resources, Software, Visualization, Writing-original draft.