긴급후진 운전이 프로펠러 축 거동에 미치는 영향
초록
추진효율을 위한 고출력 저속엔진의 채택과 설계 최적화를 위한 얇아진 선체는 추진축계의 안정성 관점에서는 부정적인 영향으로 작용하고 있다. 선체 변형은 발생하기 쉬워졌으나 추진축은 증가된 전달 토크의 영향으로 직경이 커져 구조적 변형에 유연하게 반응하기가 더욱 어려워졌기 때문이다. 이러한 현대 축계의 설계 특징에서도 축계의 안정성을 보장하기 위해서는 축계정렬 계산에 보다 적극적인 동적 상태의 고려가 필요하다. 따라서 본 연구에서는 스트레인 게이지와 변위 센서를 이용하여 과도 동적 상태의 하나인 긴급후진이 프로펠러 축 거동에 미치는 영향을 고찰하였다. 그 결과, 긴급후진 운전은 수직 방향의 프로펠러 축 거동에 상당한 영향을 미치는 것으로 나타났으며, 축계의 안정성을 향상시키기 위해 과도 상태를 포함한 동적 상태를 고려하는 것이 필요할 것으로 확인되었다.
Abstract
High-power, low-speed engines for propulsion efficiency and thinner hull for design optimization negatively affect the stability of propulsion shafting system. The reason for this is that the shaft with larger diameter to transfer increased torque becomes less flexible, while the hull becomes easier to be deformed. To ensure the reliability of shafting system even with the aforementioned designs, dynamic conditions need to be considered proactively in the calculation of shafting alignment. In this study, the effect of one specific dynamic condition, crash astern, on the propeller shaft behavior was examined using strain gage and displacement sensor. The results revealed that crash astern significantly influence the vertical behavior of the propeller shaft, indicating the need to consider dynamic conditions, including transient modes, to enhance stability of shafting system.
Keywords:
Strain Gage, Shaft Behavior, Crash Astern, Stern Tube Bearing, Marine Shafting키워드:
스트레인 게이지, 축거동, 긴급후진, 스턴 튜브 베어링, 선박 추진축계1. 서 론
추진축계정렬(propulsion shafting alignment)은 선박의 안전한 운전을 담보하기 위해 매우 중요한 부분이다. 이와 관련하여 1950년대 후반 미국 해군 함정의 축계 손상과 설계 개선에 관한 연구1,2)가 시작된 이래로 1970년대까지 자유곡선배치법과 전산프로그램 개발 등 축계 배치 최적화를 위한 다양한 연구3-7)가 진행되어 현재의 축계 정렬 이론이 확립되었다.
그러나 근래에 들어 선박들이 친환경, 고효율 관점에서 최적화된 설계 특징을 갖게 되면서 이는 축계 정렬 관점에서는 축계의 안정성을 위협하는 요소가 되고 있다. 먼저 추진효율 향상시키기 위해 주기관을 초장행정화, 저속화시킴에 따라 상대적으로 프로펠러는 대형화되고 지지 베어링에 더 큰 하중이 작용하게 되었다. 또한 선체가 설계 최적화를 위해 두께가 얇아져 변형하기 쉽게 된 반면, 고출력의 주기관 토크를 전달하기 위해 축계의 직경은 증가되어 강성이 커지면서 추진축은 선체 변형에 비교적 유연하게 대응하지 못하게 되었다.8,9) 따라서 현대의 추진 축계에는 작은 변형일지라도 안정성을 저해하는 위험요소가 될 수 있으므로 추진 축계 배치의 설계 및 시공에 있어 더욱 유의가 필요한 실정이다.
이에 대한 대응으로써 선체 변형 영향과 선미관 후부 베어링의 선미단 국부하중 완화 및 최소 유막 두께 유지 등에 관한 일련의 연구10-18)가 활발하게 진행되고 있으나, 선미관 후부 베어링 손상 사례는 여전히 보고되고 있다.19)
관련하여 동적 또는 과도상태에서 발생하는 프로펠러 편심 추력의 변동(eccentric thrust force fluctuation)이 이러한 손상을 초래할 개연성이 있음이 확인되고 있는데,20-25) 이는 표준화된 준-정적 상태(quasi-static state)의 축계정렬 계산 방식에는 적극적으로 고려되고 있지 않은 요소이다.
준-정적 상태 방식의 계산이란 축계는 정적인 상태로 두고 선박의 계획 최대 속력(Maximum Continuous Revolution, MCR)으로 운항 시에 프로펠러에서 발생하는 힘과 모멘트를 정적 상태에 반영하는 계산 방식을 말한다. 이 방식의 계산은 비교적 간단하여 시간과 비용 관점에서 이점이 있고, 축의 변형량을 용이하게 추정할 수 있는 반면, 상기에서 언급한 동적 또는 과도상태의 프로펠러 기진력에 의해 발생할 수 있는 잠재적 위험요소까지 식별하기에는 한계가 있다.
선행 연구26-28)에서는 이와 같은 한계를 해소하고, 축계 안정성을 더욱 확보하기 위해서는 실질적인 동적상태를 고려하여 선회(turning)와 같은 과도상태(transient) 시 프로펠러 하중 변화가 추가적으로 검토되어야 한다는 필요성을 보여 주고 있다.
따라서 이번 연구에서는 기존 연구에서 다루어지지 않았던 긴급후진 운전을 운항 조건으로 설정하여 실질적 동적 상태에서 프로펠러 하중 변화가 축 거동에 미치는 영향을 계측·분석함으로써, 동적 상태를 고려한 추진축계 배치 설계 기술 고도화를 위한 통계적인 기반을 마련하고자 한다.
2. 연구 방법
2.1 대상 선박 및 계측 장치의 구성
본 연구는 50,000 DWT급 중형 유조선을 대상으로 진행되었으며, 선박의 추진계 주요 사양과 베어링 위치는 Table 1, 2와 같다. 해당 축계에는 선미관 후부 베어링에 단일 경사 보링이 적용되었고 선미관 전부 베어링은 설치되지 않았다.
긴급후진 운전이 프로펠러 축 거동에 미치는 영향을 보다 정확히 확인하기 위해서는 프로펠러 부근에 수직, 수평 방향으로 변위 센서를 설치하여 궤적 변동을 구하는 것이 이상적이나, 이를 수행하기 위해서는 전용 브라켓 제작 등 실질적 제약이 있으며 부가적인 요소가 요구된다.29) 따라서 스트레인 게이지를 가능한 한 프로펠러에 가깝게하여 프로펠러 축에 설치하고 수직, 수평 방향의 굽힘모멘트를 구함으로써 프로펠러 축 거동을 추정하는 대안의 방법을 사용하였다.
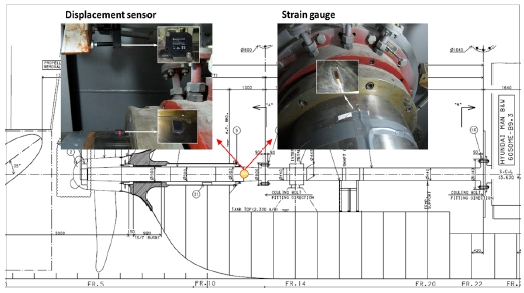
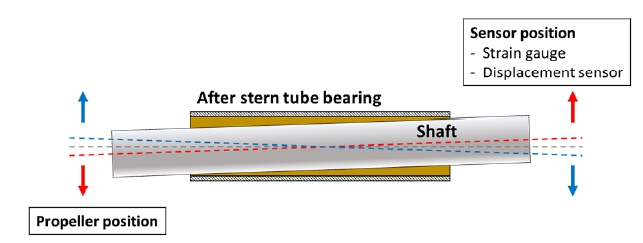
계측 장치의 설치 위치는 Fig. 1과 같다. 스트레인 게이지는 계측 중 굽힘모멘트를 도출하기 위한 용도이며, 위치 센서는 축의 회전속도계측과 굽힘모멘트를 1회전 단위로 나누어 분석하기 위한 용도이다.
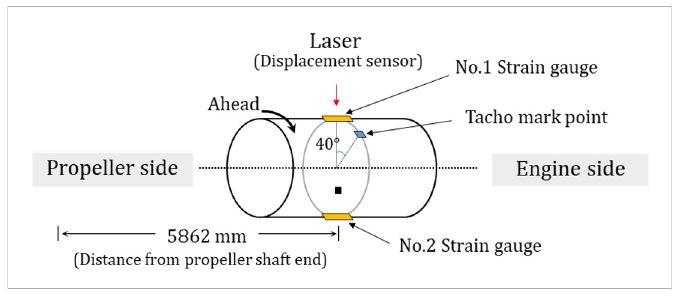
보다 상세한 센서의 부착 위치를 Fig. 2에서 보여 준다. 1회전마다의 기준점이 되는 회전수 계측용(tacho) 마크를 No.1 실린더의 상사점(Top Dead Center, TDC)와 일치하게 부착하였으며, 스트레인 게이지는 TDC보다 시계방향으로 40°만큼 뒤쳐지는 점에 설치되었다. 스트레인 게이지는 하프 휘스톤 브릿지(half wheatstone bridge) 결선 방식을 적용, 180°의 간격으로 서로 마주 보게 설치하였다.
적용된 센서의 사양은 Table 3과 같다.
2.2 실선 계측 절차 및 조건
본 연구에서는 선박의 과도(transient) 운전 모드의 하나인 긴급후진 운전을 계측 조건으로 하였다. 긴급후진 운전이란 선박에서 충돌을 피하기 위해 주기관을 비상 후진 작동하는 것을 말한다.
계측 절차로는 전속 전진 속도로 시작하여 선속이 0노트(knots)가 될 때까지 진행하는 일반적인 해상 시운전 시험 방법을 따랐으며, 이에 더하여 실제로 선박이 후진 방향으로 움직이는 때까지 연장하여 진행하였다. Table 4는 계측 중 선박 운항 단계를 선속 방향 및 추력 방향과 함께 보여 준다.
축계정렬의 안정성을 검토하기 위한 측면에서는 선체 변형을 야기하는 흘수 조건이 중요한 요소로 작용하게 되는데, 이번 계측은 타 흘수에 비해 프로펠러 편심추력이 상대적으로 큰 발라스트 흘수 상태에서 진행되었다.
2.3 축 거동 경향 해석 방법
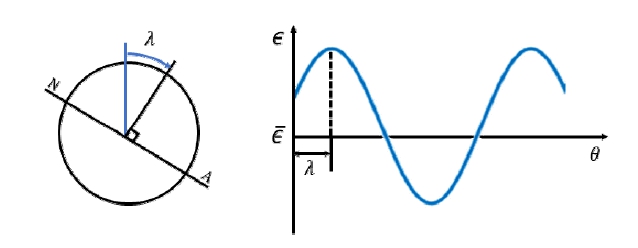
스트레인 게이지법30)을 사용하면 계측된 변형률을 축의 회전 중의 굽힘모멘트로 환산할 수 있고, 이를 1회전 마다의 수직 및 수평 성분으로 나누어 분석하면 계측 중의 축 거동 양상을 도시할 수 있다. Fig. 3에서는 축이 회전 시에 전형적으로 보이는 사인파의 변형률 곡선을 나타내며 이를 식으로 표현하면 식 (1)과 같다.
| (1) |
εa, 변형률의 진폭
, 평균 변형률
θ, 축의 수직 방향과 스트레인 게이지 사이의 각
λ, 굽힘 각, 축의 수직 방향과 중립축(N-A)의 직교지점 사이의 각
축의 응력 σ는 재료역학에서 사용되는 보의 관계식인 식 (2)와 같이 나타낼 수 있는데, 이를 변형하면 식 (3)과 같이 되어 굽힘모멘트 M을 구할 수 있다.
| (2) |
| (3) |
여기서, I는 축의 단면 2차 모멘트이고, c는 축 단면의 반지름이다. 해당 축계는 중실축으로 축의 외경 do만 반영하여 식 (4)와 같이 정리하고 1회전마다의 굽힘모멘트를 구한다.
앞의 관계식을 바탕으로 식 (5)와 식 (6)을 이용하면 굽힘모멘트의 수직 및 수평 성분을 분리할 수 있으며, 이를 통해 계측 위치에서의 프로펠러 축의 상하, 좌우 방향 거동 경향을 확인할 수 있다.
| (4) |
| (5) |
| (6) |
3. 결 과
3.1 굽힘모멘트와 굽힘각의 변화 특성
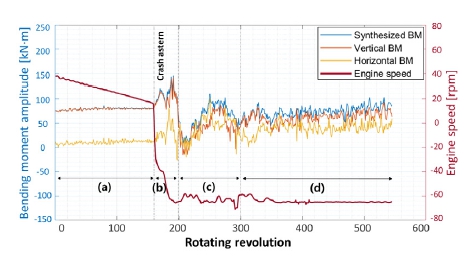
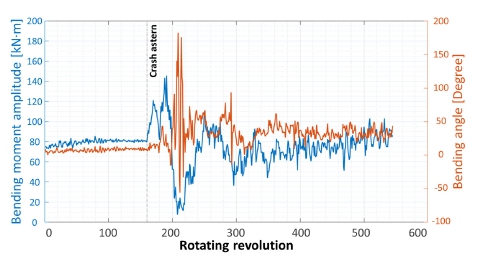
Fig. 4는 긴급후진 운전을 실시하는 중에 프로펠러 축에서 나타나는 굽힘모멘트의 변화를 회전속도와 함께 보여 준다.
Fig. 4에서 Synthesized BM은 합성 굽힘모멘트, Vertical BM은 굽힘모멘트의 수직 성분, Horizontal BM은 굽힘모멘트의 수평 성분이다.
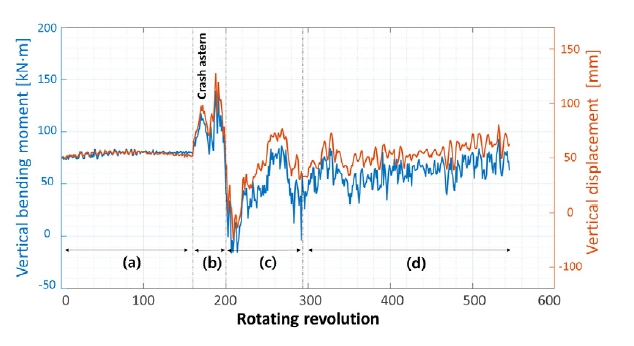
거동 해석을 용이하게 하기 위하여 수직 방향의 굽힘모멘트의 경향이 확연하게 전환되는 지점을 기준으로 하여 (a)부터 (d)까지 4단계로 구간을 나누었다. 해당 지점을 기준으로 한 이유는 긴급후진 시 굽힘모멘트의 수직 성분이 가장 영향을 많이 받는 응답 특성을 보였기 때문이다.
(a) 구간은 엔진이 정지하였으나 관성으로 인해 전진 방향으로 회전을 계속하고 있는 구간이다. 이 구간에서의 굽힘모멘트 크기는 변동 폭이 거의 없으나 속도가 줄어들수록 그 크기가 소폭 상승하고 있다. 이때의 합성 굽힘모멘트는 대부분 굽힘모멘트의 수직 성분과 같고, 수평 성분은 0 kNm에 가깝다. 긴급후진이 시작된 직후인 (b) 구간에서는 수직 성분의 굽힘모멘트는 바로 반응하면서 그 크기가 약 140 kNm까지 커졌으며, 수평성분의 경우에는 역회전 직후 바로 반응하지는 않고 약 20회 가량 회전 후 순간적으로 크기가 커졌다.
(c) 구간에서는 두 성분 모두 급격하게 줄어들었다가 다시 커지는 과도한 변동 특성을 보였고, (d) 구간에서는 변동 폭이 줄면서 대체로 평균적인 크기를 띄며 비교적 안정적으로 운전하는 형태를 보였다.
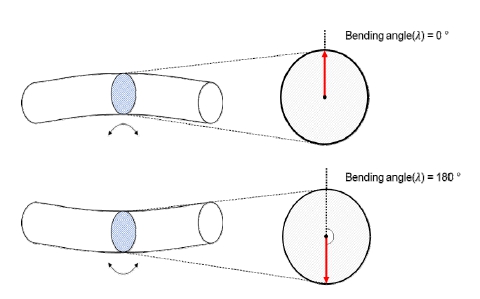
계측 중의 굽힘각 변화 특성은 Fig. 5와 같으며, 굽힘각과 그 방향에 대한 기준은 Fig. 6과 같이 설정하였다. 굽힘각은 계측 초기의 엔진 정지상태에서는 0°에 가깝게 유지되며 주로 프로펠러 하중으로 인한 처짐의 영향만 받고 있다가 긴급후진 직후 큰 폭으로 변동하는 특성을 보였다. 이때, 굽힘각이 90°가 넘으면서 가장 크게는 180°에 가까운 값이 확인되었는데, 이는 곧 축의 양단이 들리면서 U자 형태로 굽히는 것을 말한다.
이러한 굽힘 형태는 프로펠러 무게에 의해 양단이 처지는 일반적인 프로펠러 축 굽힘과 반대이다. 과도한 변동을 보이는 구간 이후 축은 평균 약 40°로 수렴하는 굽힘각을 이루며 회전하였다.
3.2 프로펠러 축의 궤적 선도
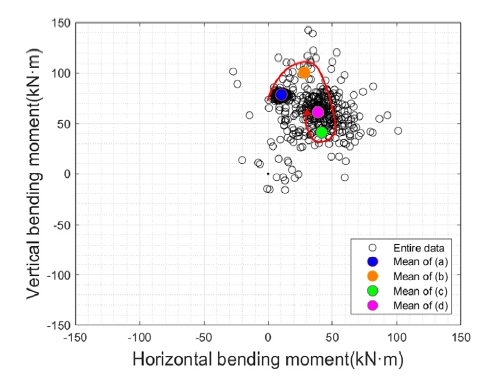
상기와 같이 도출된 수직 및 수평 성분의 굽힘모멘트를 궤적 선도로 표현하면 Fig. 7과 같다. 검정색의 원으로 표시된 전체 데이터(entire data)는 계측 전체 구간의 데이터를 나타낸다. 주로 우측 상방에 그 궤적을 보였다.
이를 앞서 구분한 구간으로 나누어 각 구간에서의 평균값을 사용하여 검토해 보면, 먼저 엔진이 정지한 (a) 구간에서는 수평 방향으로는 거의 중앙에 위치하고 수직 방향으로는 상방에 위치하였다.
Crash astern 직후인 (b) 구간에서 우측 상방으로 이동하였다가 (c) 구간에서는 우측 하방으로 이동하는데 특히 하방으로 매우 큰 폭의 움직임을 보였다. 이후 (d) 구간에서는 상방으로 약간의 움직임을 보였다.
이처럼 대상 선박에 있어 긴급후진 운전은 프로펠러 축 거동에 있어 유의미한 영향을 미치는 과도 동적 상태임을 확인하였으며, 수평 방향의 거동에 비해 특히 수직 방향의 거동이 매우 두드러짐을 알 수 있었다.
3.3 변위센서를 이용한 결과의 교차 검증
결과의 교차 검증을 위해 수직 성분의 굽힘모멘트와 변위 센서로 계측한 상하 방향 변위 데이터를 Fig. 8에 함께 나타내었다. 도출 및 계측한 데이터를 서로 비교하였을 때, 변동이 매우 일치하는 경향을 보이며 유효성이 확인되었다.
다만, 변위 센서의 설치 수량 문제로 수평성분의 교차 검증은 진행할 수 없었으며, 동 사항은 추후 연구를 통해 보완할 필요가 있음이 식별되었다.
4. 고 찰
프로펠러축을 Fig. 9와 같이 변형이 없는 직선보로 가정하고 계측 위치에서의 움직임(sensor position)을 상하, 좌우로 반전하면 프로펠러 위치(propeller position)에서의 축 거동을 추론할 수 있다.22,23)
위와 같은 추론 방식으로 Fig. 7에서의 궤적 선도를 고찰해 보면, 계측 중 프로펠러 위치에서의 축은 중앙 하방에서 시작하여 좌하방-좌상방-우하방 순으로 거동한다.
먼저 엔진이 정지한 (a) 구간에서는 수평방향으로는 중앙에 가까우면서 수직 방향으로는 하방에 위치하며 선미관 후부 베어링을 누르는 하중으로 작용하고 있었으며, 이후 (b) 구간에서는 긴급후진 운전 시작과 함께 베어링의 지지 하중을 더욱 증가시키는 방향인 좌측 하방으로 거동하였다. 이는 곧 긴급후진 직후 베어링의 안정성은 부정적인 영향을 받는 것으로 판단된다.
다음으로 (c) 구간에서는 축이 매우 급격하게 상방으로 움직이는 과도한 거동 형태를 띄었다. 이는 엔진 가속, 선회 등의 동적 상태를 운전 조건으로 하여 프로펠러 축 거동을 고찰한 기존 연구에서는 확인되지 않았던 긴급 후진 시의 특징적인 거동으로 보인다. 이러한 거동은 선미관 후부 베어링의 선미단 국부하중이 완화되는 방향이기는 하나, 안정적인 구간의 축 거동에 비해 매우 큰 폭으로 변동하여 베어링 후부 상단과 전부 하단에는 오히려 부정적인 하중으로 작용할 가능성이 있을 것으로 판단되며, 이와 관련해서는 후속연구가 필요할 것으로 보인다.
마지막으로 (d) 구간에서는 우측 하방으로 비교적 소폭의 움직임을 보였다.
계측 중 선속을 함께 측정하지 못하여 정확하게 특정하기는 어렵지만 대체로 과도한 거동 특성을 보이는 구간은 Table 4의 ② 단계인 reverse/ahead 구간으로 추정된다.
이 단계에서는 프로펠러의 추력 방향과 선박 항해 방향이 서로 반대가 되면서 프로펠러 블레이드 끝단에서는 고리형 와류(ring voltex)가 발생하는 등 순간적으로 선체 후부 및 프로펠러 부근의 유체 흐름이 변한다.31-37) 이러한 불균일한 반류가 본 연구 결과와 같은 프로펠러 축의 과도 거동 특성에 영향을 미칠 수 있으며, 이후 reverse/reverse 구간이 시작되면서 선미에서의 유체 흐름이 같은 방향으로 되어 안정적인 거동 형태를 보였을 것으로 판단된다.
5. 결 론
본 연구에서는 중형 유조선을 대상으로 스트레인 게이지와 변위 센서를 사용하여 과도운전모드 중 하나인 긴급후진 운전이 프로펠러 축 거동에 미치는 영향을 고찰하였으며, 다음과 같은 결과를 얻었다.
1) 스트레인 게이지법을 이용하여 회전 중인 축의 수직, 수평 방향의 굽힘모멘트를 도출할 수 있었다. 이를 통해 해당 축계의 거동 경향을 추정하였으며, 그 결과의 신뢰성은 변위 데이터를 통하여 교차 검증되었다.
2) 긴급후진 운전은 프로펠러 축 거동에 큰 영향을 미치는 운전 조건임이 확인되었고, 특히 상하 방향으로의 움직임에 있어 과도한 응답특성을 보였다. 이러한 과도응답 상태는 프로펠러는 후진 추력을 발생시키지만 선박은 여전히 관성에 의해 전진하고 있는 상태인 reverse/ahead 구간에서 유의미하게 나타났으며, 특히 이 구간 중 프로펠러가 상방으로 튀어 오르는 형태의 축 거동은 긴급후진 운전에서 보이는 특징적인 과도거동 특성으로 확인되었다. 이는 선미관 후부 베어링 선미측 끝단에 일시적으로 과도한 국부 하중이 인가됨을 의미한다.
3) 이처럼 긴급후진 운전이 축의 거동 방향과 범위를 급변하게 하는 운전으로 축의 안정성 유지에 부정적 영향을 주는 요소로 식별됨에 따라, 축의 안정성을 담보하기 위해서는 상기와 같은 동적 과도상태에서의 급격한 프로펠러 편심추력 변화가 축계 배치 설계 단계에서 중요하게 고려될 필요가 있다고 판단된다.
4) 다만, 이번 연구는 특정 선박의 특정 조건에서 수행한 결과이므로 이후 선종, 운전 조건, 흘수 조건을 다양화하는 방향으로의 후속 연구를 지속하여 동적 과도상태에서 발생하는 위험 요소의 통계적 기반을 마련해 나갈 학문적 필요가 있다.
Acknowledgments
본 연구는 해양수산부와 해양수산과학기술진흥원 연구비 지원으로 수행된 ‘자율운항선박 기술개발사업(2020615)’과 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다.(No. 2021R1F1A1047115) 이에 감사드립니다.
Author contributions
J. H. Jeong; Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Resources, Writing-original draft. J. U. Lee; Funding acquisition, Project administration, Supervision, Validation, Writing-review & editing.
References
-
J. J. Francis, R. E. Kosiba and R. A. Woollacott, 1956, “The Alignment of Main Propulsion Shaft Bearings in Ships”, Journal of the American Society for Naval Engineers, 68(3), 515-526.
[https://doi.org/10.1111/j.1559-3584.1956.tb05269.x]

-
R. Michel, 1959, “A quarter century of propulsion shafting design practice and operating experience in the U.S. navy”, The Journal of the American Society of Naval Engineers (NEJ), 71(1), 153-164.
[https://doi.org/10.1111/j.1559-3584.1959.tb05306.x]

-
G. Mann, 1964, “Design of propulsion shaft systems using fair curve alignment theory”, The American Society of Naval Engineers Journal (NEJ), 76(6), 851-862.
[https://doi.org/10.1111/j.1559-3584.1964.tb04091.x]

-
G. Mann, 1965, “Analysis of shafting problems using fair curve alignment theory”, The American Society of Naval Engineers Journal (NEJ), 77(1), 117-133.
[https://doi.org/10.1111/j.1559-3584.1965.tb05656.x]

-
G. Mann, 1965, “Shipyard alignment of propulsion shafting using fair curve alignment theory”, The American Society of Naval Engineers Journal (NEJ), 77(4), 651-659.
[https://doi.org/10.1111/j.1559-3584.1965.tb04996.x]

- M. D. Hong and H. J. Joen, 1981, “A Study on the Propulsion Shaft Alignment Calculation by the Matrix Method of Three-Moment Theory”, Journal of Advanced Marine Engineering and Technology, 5(1), 20-27.
- T. I. Park and H. Y. Lee, 1979, “Alignment Calculation of Marine Engine Shafting System by Quadruple Integration Method”, Journal of Advanced Marine Engineering and Technology, 3(1), 32-39.
- American Bureau of Shipping (ABS), 2006, Guidance Notes on Propulsion Shafting Alignment, NY, USA: ABS.
- Nippon Kaiji Kyokai (NK), 2006, Guidelines on Shafting Alignment, Japan: NK.
-
K. H. Low and S. H. Lim, 2004, “Propulsion shaft alignment method and analysis for surface crafts”, Advances in Engineering Software, 35(1), 45-58.
[https://doi.org/10.1016/S0965-9978(03)00082-6]

- D. Šverko., 2005, “Hull deflections shaft alignment interaction, a case study”, Proceedings of the 7th International Symposium on Marine Engineering, 24-28.
-
L. Shi, D. Xue and X. Song, 2010, “Research on shafting alignment considering ship hull deformations”, Marine Structures, 23(1), 103-114.
[https://doi.org/10.1016/j.marstruc.2010.01.003]

-
J. U. Lee, 2016, “A study of the analysis of shaft alignment considering hull deflections for 50,000 DWT oil/chemical tankers”, Journal of Advanced Marine Engineering and Technology, 40(3), 191-197.
[https://doi.org/10.5916/jkosme.2016.40.3.191]

-
C. O. Seo, J. U. Lee, J. H. Kim and J. R. Kim, 2018, “A study on the hull deflections affecting propulsion shafting alignment for a 173,000 CBM liquefied natural gas carrier”, Journal of Advanced Marine Engineering and Technology, 42(4), 258-264.
[https://doi.org/10.5916/jkosme.2018.42.4.258]

-
C. O. Seo, J. U. Lee, J. H. Kim and J. R. Kim, 2019, “A study on hull deflections affecting the propulsion shafting alignment of a 300,000 DWT crude oil tanker”, Journal of Advanced Marine Engineering and Technology, 43(3), 163-170.
[https://doi.org/10.5916/jkosme.2019.43.3.163]

-
D. S. Cho, H. K. Jang, B. M. Jin, K. Kim, S. C. Kim and J. H. Kim, 2016, “Propulsion Shafting Alignment Analysis Considering the Interaction between Shaft Deflection and Oil Film Pressure of Sterntube Journal Bearing”, Journal of the Society of Naval Architects of Korea, 53(6), 447-455.
[https://doi.org/10.3744/SNAK.2016.53.6.447]

-
J. U. Lee, B. Jeong and T. H. An, 2019, “Investigation on effective support point of single stern tube bearing for marine propulsion shaft alignment”, Marine Structures, 64, 1-17.
[https://doi.org/10.1016/j.marstruc.2018.10.010]

-
J. S. Sun, Y. G. Kim and U. K. Kim, 2021, “Study on shaft alignment of propulsion shafting system depending on single reaction force supporting position of aft stern tube bearing”, Journal of Marine Science and Technology, 26(4), 1340-1357.
[https://doi.org/10.1007/s00773-021-00803-3]

-
G. Park, C. Koh, J. Chung, G. Nam and J. Chae, 2021, “A Study on the Stern Bearing Damage and Shaft Alignment for 37K DWT Product/Chemical Tanker”, Journal of the Society of Naval Architects of Korea, 58(2), 97-104.
[https://doi.org/10.3744/SNAK.2021.58.2.097]

- R. Kuroiwa, A. Oshima, T. Nishioka, T. Tateishi, K. Ohyama and T. Ishijima, 2007, “Reliability improvement of stern tube bearing considering propeller shaft forces during ship turning”, Mitshbishi Heavy Industries, Ltd. Technical Review, 44(3), 1-5.
- B. J. Vartdal, T. Gjestland and T. I. Arvidsen, 2009, “Lateral propeller forces and their effects on shaft bearings”, First International Symposium on Marine Propulsors, 475-481.
-
J. W. Lee, Q. D. Vuong, B. Jeong and J. U. Lee, 2022, “Changes in propeller shaft behavior by fluctuating propeller forces during ship turning”, Applied Sciences, 12(10).
[https://doi.org/10.3390/app12105041]

-
Q. D. Vuong, J. W. Lee, W. J. Lee, H. Choi, K. Seo, Y. Kim, J. H. Jeong and J. U. Lee, 2022, “Establishing the True Dynamic Bending Moment of Propeller Shaft Using a Single Bridge of Strain Gauge”, Applied Sciences, 12(18).
[https://doi.org/10.3390/app12189235]

-
S. H. Shin, 2015, “Effects of Propeller Forces on the Propeller Shaft Bearing during Going Straight and Turning of Ship”, Journal of the Society of Naval Architects of Korea, 52(1), 61-69.
[https://doi.org/10.3744/SNAK.2015.52.1.61]

-
J. U. Lee, 2018, “Application of strain gauge method for investigating influence of ship shaft movement by hydrodynamic propeller forces on shaft alignment”, Measurement, 121, 261-275.
[https://doi.org/10.1016/j.measurement.2018.02.067]

-
G. Dubbioso, R. Muscari, F. Ortolani and A. Di Mascio, 2017, “Analysis of propeller bearing loads by CFD. Part I: straight ahead and steady turning maneuvers”, Ocean Engineering, 130, 241-259.
[https://doi.org/10.1016/j.oceaneng.2016.12.004]

-
R. Muscari, G. Dubbioso, F. Ortolani and A. Di Mascio, 2017, “Analysis of propeller bearing loads by CFD. Part II: Transient maneuvers”, Ocean Engineering, 146, 217-233.
[https://doi.org/10.1016/j.oceaneng.2017.09.050]

- T. G. Lee, G. S. Song, J. N. Kim, J. S. Lee and H. G. Park, 2017, “Effect of propeller eccentric forces on the bearing loads of the complicated shafting system for large container ships”, In Fifth International Symposium on Marine Propulsors, 17.
- B. S. Yang, 2006, “Condition Monitoring & Diagnostics”, Intervision.
-
A. W. Forrest and R. F. Labasky, 1981, “Shaft alignment using strain gages”, Marine Technology and SNAME News, 18(3), 276-284.
[https://doi.org/10.5957/mt1.1981.18.3.276]

- P. J. Pontaza, H. C. Chen and S. K. Lee, 2006, “Chimera Reynolds-Averaged Navier-S tokes simulations of coupled ship and propeller flows”, The Sixteenth International Offshore and Polar Engineering Conference.
- H. C. Chen and S. K. Lee, 2003, “Chimera RANS simulation of propeller-ship interactions including crash-astern conditions”, The Thirteenth International Offshore and Polar Engineering Conference.
- S. K. Lee, 2006, “CFD simulation for propeller four-quadrant flows”, SNAME 11th Propeller and Shafting Symposium.
- P. Kumar and K. Mahesh, 2015, “Analysis of marine propulsor in crashback using large eddy simulation”, Fourth International Symposium on Marine Propulsors.
- M. Pontarelli, J. E. Martin and P. M. Carrica, 2017, “Dynamic instabilities in propeller crashback”, Proceedings of 5th International Symposium on Marine Propulsors.
-
M. Vysohlid and K. Mahesh, 2006, “Large eddy simulation of crashback in marine propellers”, 44th AIAA Aerospace Sciences Meeting and Exhibit.
[https://doi.org/10.2514/6.2006-1415]

- S. K. Lee, M. Liao and S. Wang, 2006, “Propeller-induced hull vibration—analytical methods”, Proceedings of the second international ship noise and vibration conference, 28.