크랭크축 각속도를 이용한 기계학습 기반 연소실 압력 예측

1. 서 론

역사적으로 연소실 압력 데이터는 엔지니어들이 내연기관의 상태를 파악하기 위해 사용되었으며, 1960년대 전자 압력 센서가 개발되면서 엔진에서 발생하는 완전한 압력 사이클을 측정하는 것이 가능해졌다. 그리고 전자 압력 센서와 마이크로프로세서(CPU)의 발전으로 연소실 압력이란 변수를 활용할 가능성이 제시되면서 엔진 제어 및 모니터링, 연소해석 분야에 많은 연구가 시작되었다.¹⁾ 선박 엔진의 연소실 압력은 일반적으로 연소 진행에 대한 정량적 정보로서, 도시 평균유효압력(Indicated Mean Effective Pressure, IMEP) 및 열방출 속도(Rate of Heat Release)를 계산하기 위해 사용되어지며, 이를 통해 최적의 점화지점과 엔진 상사점(Top Dead Center, TDC)의 위치설정의 오차를 분석할 수 있다.²⁾ 또한 연소실 압력을 통해 선박 엔진 점화 시점을 설정하여 노크를 제어하며 출력을 높이고, 실린더 내 불완전 연소상태를 파악하여 배출가스 감축 및 고장진단을 할 수 있는 중요한 정보이다.^3-5)

하지만 선박뿐만 아니라 실제로 밀폐된 내연기관의 연소실 압력을 직접 계측 장비로 측정하는 것은 어려운 작업이다. 그리고 2000년대 이후 해운산업에서는 선박의 대형화 추세와 함께 연소실 최고폭발압력 역시 증가하였다. 따라서 선박 엔진 주변의 높은 온도와 선체 진동의 요인에 의해 전자 압력 센서는 고품질의 비싼 센서를 엔진의 각 실린더에 사용해야 하고, 정기적으로 보정작업이 필요하여 높은 유지보수 비용이 발생하는 문제점이 있다.

최근 선박의 상태 예측에 관한 연구 동향은 선박에서 발생한 데이터 및 인공지능 기술을 결합하여 주로 불완전 연소와 같은 고장진단을 판단하는 연구⁶⁾ 또는 단일 실린더의 고속 소형엔진을 대상으로 연소실 압력을 예측한 연구^7,8)들이 있으며, 선박과 같이 대형 저속엔진을 대상으로 다중의 연소실 압력 상태를 예측하는 연구는 부족한 실정이다. 또한 대부분의 선박용 중소형 엔진의 경우 연소실 압력을 직접 측정할 수 있는 테스트콕(Test cock)이 설치되지 않아 센서의 고장 시 압력 측정이 불가능하다.

따라서 본 논문에서는 연소실 압력 센서의 고장 시 이를 백업으로 사용하고 정확한 연소실 압력을 예측할 수 있는 기술을 개발하고자 한다. 이를 위해 상대적으로 저렴한 엔코더(Encoder)를 통해 엔진의 크랭크축 각속도 데이터를 취득하고, 인공지능 기술과 결합하여 엔진의 연소실 압력을 간접적으로 예측할 수 있는데 목적이 있다.

2. 연구 방법

2.1 대상선박과 측정장치의 구성

Table 1은 대상선박의 엔진사양이며, MAN사의 6개 실린더가 장착된 엔진 및 가변피치프로펠러가 설치되어있다.

Table 1

Specification of the main engine

Fig. 1은 본 연구의 실험장치에 대한 개략도이며, Table 2는 실험장비에 대한 사양을 나타낸다. 실험 데이터의 정밀도를 높이고자 수집속도(Sampling rate)를 4,167 S/sec로 충분하게 설정한⁹⁾ 이후 데이터를 측정하였다. 연소실 및 소기 압력은 전자 압력 센서의 신호를 실험장치연소실 및 소기압력은 실험장치와 병렬로 연결하고, 증폭기(Amplifier)를 거쳐 데이터를 취득하였다. 크랭크축의 각속도는 1번 실린더 상사점 위치에 1회전당 1회 펄스를 발생하는 엔코더의 Z 펄스를 일치시켜 취득하였다. 엔진의 부하는 추진축에 스트레인 게이지(Strain gauge)를 설치하여 토크(Torque) 및 부하를 계산하였다.

Fig. 1

Overall experimental setup

Table 2

Specifications for the experimental equipment

2.2 실험 절차

Table 3은 데이터 취득 시 설정한 선박의 시험절차를 나타낸다. 엔진의 약 10~70% 부하에서 크랭크축 각속도, 소기압력, 연소실 압력의 변화를 확인하기 위해 가속 및 부하가 일정한 구간으로 구분하여 데이터를 측정하였다.

Table 3

Measurement scheme for experiment

2.3 기계학습 방법

Fig. 2는 본 연구의 기계학습 절차를 나타낸다. 측정한 데이터에서 감도(Sensitivity) 및 오프셋(Offset)을 연산하고, 고속 푸리에 변환(Fast Fourier Transform, FFT), 데이터 필터링(Filtering) 및 평활화(Smoothing)를 통해 잡음(Noise) 처리를 한 후, 크랭크 각도 기준으로 데이터를 리샘플링(Resampling)하는 데이터 전처리 과정을 거쳤다. 이후 기계학습 방법 중 심층 신경망((Deep Neural Network, DNN) 모델을 적용하기 위해 데이터를 분류하고, 최적의 모델 파라미터를 저장하기 위해 특성 스케일링(Feature scaling), 교차검증(Cross validation), 하이퍼 파라미터(Hyper parameter) 탐색의 과정을 거쳐 최종적으로 학습한 모델을 저장하였다. 그리고 최종 모델의 성능을 회귀분석의 성능지표로 평가하고, 예측한 연소실 압력과 실제 연소실 압력을 비교하였다. 또한 연소실 압력을 이용한 엔진의 출력을 계산 및 비교하여 그 결과를 확인하였다.

Fig. 2

Flow chart for machine learning

2.3.1 심층 신경망

본 연구에서는 예측하고자 하는 6개 실린더의 연소실 압력을 출력 변수로 설정하였고, 기계학습의 방법 중 다중의 출력 변수를 예측하기 위해서 심층 신경망 방법을 사용하였다.

심층 신경망은 Fig. 3과 같이 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)으로 구성되며 각 층의 뉴런은 완전히 연결되어 있다. 각 뉴런 사이에는 식 (1)과 같이 개별 가중치(Weight)가 존재하며, 이전 층의 각 뉴런에 출력 데이터가 곱해지고, 여기에 편향(Bias)을 더한다. 여기서 W는 가중치, Ψ는 이전 층에서의 출력 데이터, b는 편향을 나타낸다.¹⁰⁾

Fig. 3

Deep neural network schematic

$\[ T_i=\sum _{i=1}^N W_i{\Psi }_i+b \]$

(1)

심층 신경망에는 식 (1)에 적용되는 활성화 함수(Activation function)가 있으며, 신경망 내에서 각 층에 입력된 가중치 및 비선형 입력 데이터의 총합을 출력 신호로 변환하는 함수이다. 본 연구에서는 식 (2)와 같이 경사함수인 ReLU(Rectified Linear Unit), ELU(Exponential Linear Unit), 지수함수와 로그함수를 결합하여 만든 소프트플러스(Softplus) 함수를 사용하였다.

$\[ \begin{array}{l}ReLU:f\left(x\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left(0,x\right)\\ ELU:\begin{array}{ll}f\left(x\right)=x \mathrm{i}\mathrm{f} x>0& if x>0\\ f\left(x\right)=\alpha \left(e^x-1\right)& if x \le 0\end{array}\\ Softplus: f\left(x\right)=\frac{1}{\beta }*\mathrm{l}\mathrm{o}\mathrm{g}\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left({\beta }^{*}x\right)\right)\end{array} \]$

(2)

활성화 함수 이후 식 (3)과 같이 T_i는 이전 신경망 층의 출력 데이터 및 다음 층의 입력 데이터가 된다.

$\[ {\dot{\Psi }}_i=f\left(T_i\right)=f\left(\sum _{i=1}^N W_i{\Psi }_i+b\right) \]$

(3)

식 (1)~(3)은 출력 데이터를 생성하기 위해 완전히 연결된 뉴런에 대해 입력에서 출력층으로 전파되는 과정을 나타낸다. 그런 다음 최종 출력 데이터(Ψ)와 목표 데이터(y)를 비교하고, 식 (4)를 사용하여 비용함수(Cost function)를 계산한다.

$\[ C_f=\frac{1}{n}\sum y-{\Psi }^2 \]$

(4)

마지막으로 비용함수를 최소화하기 위해 역전파(Backpropagation)¹¹⁾를 통해 최적의 가중치와 편향을 결정하며, 이러한 입력층부터 출력층까지 계산되는 과정을 에포크(Epochs)라 한다.

2.3.2 데이터 전처리

1) 감도와 오프셋

Table 4는 측정한 데이터의 디지털 신호를 각 항목에 맞는 단위로 변환하기 위해 설정한 센서의 감도와 오프셋을 나타낸다.

Table 4

Sensitivity & Offset values of measurement data

2) 데이터 필터링 및 평활화

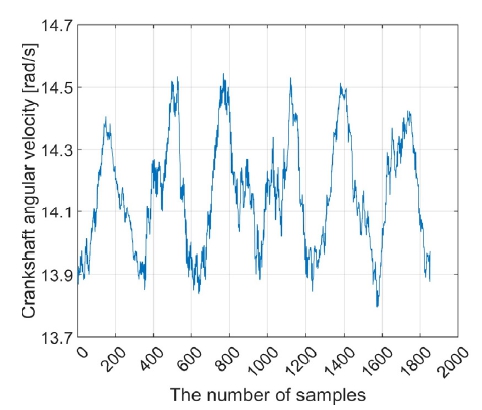
Fig. 4는 엔진 1 사이클 동안의 크랭크축 각속도 데이터를 나타내며, 엔진의 연소실 압력, 왕복 관성력을 포함하는 불평형력 또는 불평형 모멘트, 프로펠러의 불평형 질량과 변동 유체력 등의 여러 원인에 의해서 데이터 신호에 잡음이 포함된 사실과 실린더 수만큼 폭발력에 따라 증가와 감소를 반복하는 것을 확인할 수 있다.^12,13)

Fig. 4

Crankshaft angular velocity fluctuation

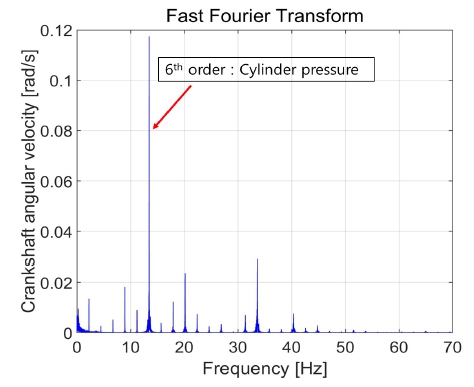
크랭크축 각속도 데이터 신호의 잡음을 제거하기 위해서 FFT를 통해 잡음이 발생하는 주파수 영역을 확인하였다. Fig. 5는 엔진의 50% 부하에서 FFT 처리한 결과이며, 6개의 실린더가 장착된 엔진에서 발생하는 6차 진동 성분으로부터 가장 큰 진폭이 발생하는 것을 확인하였다.

Fig. 5

FFT processing of crankshaft angular velocity

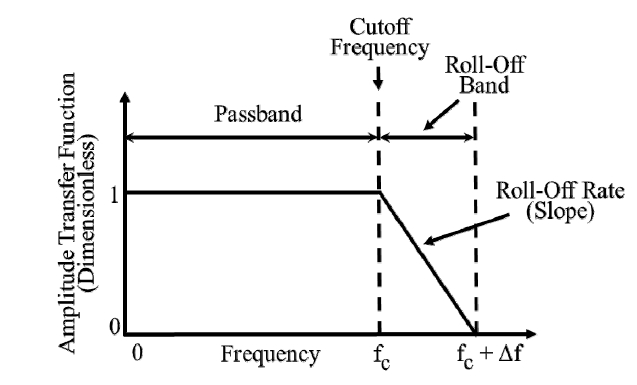
Fig. 6에서 볼 수 있듯이, FFT로 식별한 데이터 신호에서 발생하는 잡음을 제거하기 위해 저주파통과필터(Low Pass Filter, LPF)를 사용하였다. LPF는 차단 주파수 이상의 신호를 감쇠시키고 차단 주파수 이하의 주파수 신호만 통과시키는 필터이며, 본 연구에서는 차단 주파수를 엔진에서 발생한 6차 진동 성분 주파수의 2배수, ∆f를 0으로 설정하여 차단 주파수 이후 감쇠 구간이 없는 방법을 사용하였다.

Fig. 6

Low pass filter

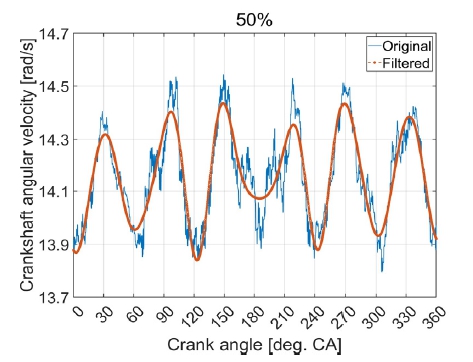
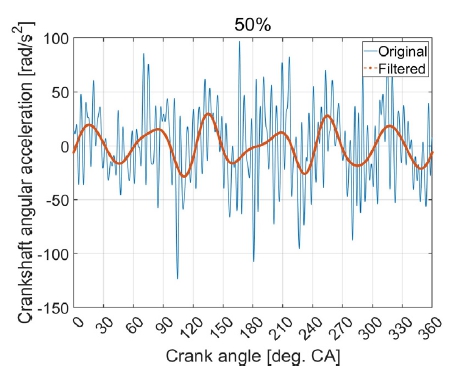
Fig. 7은 엔진의 50% 부하에서 1 사이클 동안 측정한 크랭크축 각속도와 LPF로 필터링한 데이터를 동시 비교한 그래프이다. 데이터 신호의 잡음 제거 이후 크랭크샤프트크랭크축 각속도가 뚜렷하게 실린더 수만큼 증가와 감소를 반복하는 것을 확인하였다. Fig. 8은 크랭크축 각속도를 미분하여 생성한 각가속도 데이터이며, 기계학습 시 입력 변수로 사용할 수 있도록 하였다.

Fig. 7

Comparison of crankshaft angular velocity

Fig. 8

Comparison of crankshaft angular acceleration

연소실 압력 데이터는 잡음을 효과적으로 제거하고 향상된 엔진의 성능분석을 위해 이동 평균 필터(Moving Average Filter)를 사용하여 데이터를 평활화하였다.¹⁴⁾

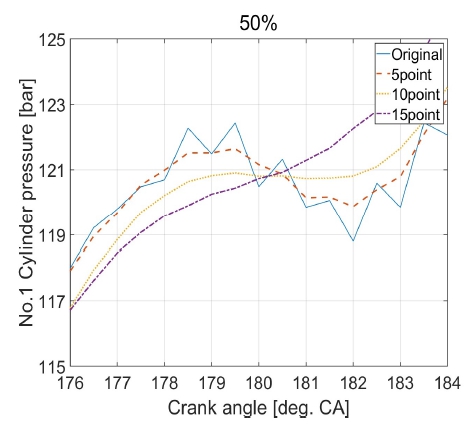
Fig. 9는 1번 실린더의 압축압력 구간을 5, 10, 15점 평활화하였을 때, 각 결과를 동시에 비교한 그래프이다. 압축압력 지점이 왜곡되지 않고 신호의 잡음을 제거할 수 있는 10점 평활화를 적용하였다.

Fig. 9

Comparison of pressure data

3) 리샘플링

엔진의 1 사이클을 나타내는데 일정하지 않은 샘플 수는 기계학습 및 엔진의 성능분석을 수행하는데 효율성과 정확성을 떨어뜨린다.¹⁵⁾ 따라서 각 엔진 부하의 1 사이클에 일정한 샘플 수 및 전체 데이터의 용량을 줄이기 위해 0.5⁰크랭크 각도 간격으로 데이터를 리샘플링하였다.

2.3.3 기계학습 모델링

데이터 전처리 과정 후 모델링을 위해 Table 5 및 Table 6과 같이 심층 신경망에 사용할 입력 변수와 출력 변수를 지정하고, 모델 학습을 위한 훈련 및 검증(Train & Validation), 테스트(Test) 데이터 세트로 분류하였다.

Table 5

Input and Output variables

Table 6

Data classification for machine learning

Table 7과 같이 입력 변수에 사용된 특성별 데이터의 규모의 크기가 다르면 출력 변수를 예측하는데 미치는 영향력의 차이가 발생하므로, 입력변수의 최솟값과 최댓값을 0~1 사이로 조정하는 “MinMax scaler”를 사용하였다. 또한 모델링 과정에서 사용자의 하이퍼 파라미터 설정에 따라 모델의 성능 차이가 발생할 수 있다. 하지만 특정 데이터의 하이퍼 파라미터를 찾는 과정은 너무도 많은 경우의 수가 발생하기 때문에 긴 시간이 소요되며, 이로 인해 최적의 인자들을 결정하는 것은 어렵다. 따라서 Table 8의 심층 신경망 하이퍼 파라미터 인자들로 구성된 243개의 조합 중에서 가장 성능이 우수한 조합을 탐색하였다. 이를 위해 각 조합에서 전체 데이터를 5등분 후 교차검증을 통해 5개의 성능평가 결과를 평균하였고, 가장 높은 점수를 받은 조합을 하이퍼 파라미터로 설정하는 “그리드 탐색(Grid search)”방법을 사용하였다.

Table 7

Input and Output variables

Table 8

Hyper parameter arguments

모델의 성능평가를 위해 식 (5)~(8)과 같이 회귀모델의 주요 성능지표 사용하였다.

$\[ \mathrm{평}\mathrm{균}\mathrm{ }\mathrm{제}\mathrm{곱}\mathrm{근}\mathrm{ }\mathrm{오}\mathrm{차}\left(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}\right)=\sqrt{\frac{1}{N}\sum _{i=1}^N {\left(y_i-\widehat{y_i}\right)}^2} \]$

(5)

$\[ \mathrm{평}\mathrm{균}\mathrm{ }\mathrm{제}\mathrm{곱}\mathrm{ }\mathrm{오}\mathrm{차}\left(\mathrm{M}\mathrm{S}\mathrm{E}\right)=\frac{1}{N}\sum _{i=1}^N {\left(y_i-\widehat{y_i}\right)}^2 \]$

(6)

$\[ \mathrm{평}\mathrm{균}\mathrm{ }\mathrm{절}\mathrm{대}\mathrm{ }\mathrm{오}\mathrm{차}\left(\mathrm{M}\mathrm{A}\mathrm{E}\right)\mathrm{ }=\frac{1}{N}\sum _{i=1}^N \left|y_i-\widehat{y_i}\right| \]$

(7)

$\[ \begin{array}{l}\mathrm{결}\mathrm{정}\mathrm{계}\mathrm{수}\left(R^2 Score\right)=\frac{SSE}{SST}=1-\frac{SSR}{SST}\\ SST=\sum _{i=1}^N {\left(y_i-{\stackrel{-}{y}}_i\right)}^2\\ SSE=\sum _{i=1}^N {\left({\widehat{y}}_i-{\stackrel{-}{y}}_i\right)}^2\\ SSR=\sum _{i=1}^N {}^2\\ \left({(y}_i: \mathrm{계}\mathrm{측}\mathrm{ }\mathrm{값}, {\stackrel{-}{y}}_i : \mathrm{계}\mathrm{측}\mathrm{값}\mathrm{의}\mathrm{ }\mathrm{평}\mathrm{균}, \widehat{y_i} : \mathrm{예}\mathrm{측}\mathrm{ }\mathrm{값}\right)\end{array} \]$

(8)

Table 9는 최종적으로 설정된 하이퍼 파라미터를 나타낸다. 하이퍼 파라미터를 적용 후 1,000에포크 동안 훈련하는 과정에서 최적의 성능을 낸 에포크 지점을 최종모델로 설정하였다.

Table 9

Final hyper parameters of DNN

3. 결 과

3.1 기계학습 모델의 성능평가

본 연구의 기계학습 모델은 입력 변수를 통해 각 실린더의 연소실 압력을 예측하는 회귀모델이다. 회귀모델에서 성능을 평가하는 주요 지표는 RMSE, MSE, MAE, R²를 사용하며 RMSE, MSE, MAE 성능지표는 0에 근접할수록, R² 성능지표는 1에 가까울수록 높은 점수를 의미한다.

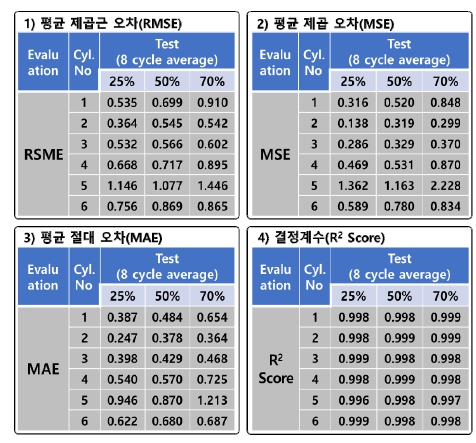
기계학습 모델의 성능평가를 위해 25%, 50%, 70% 부하에서 각 8 사이클의 테스트 데이터를 적용하였다. Fig. 10은 0.5⁰크랭크 각도 간격으로 나타난 각 실린더의 연소실 압력에 대한 예측값과 실측값을 회귀모델의 성능지표로 계산하고, 이를 평균하여 나타낸 결과이다. 엔진의 부하 및 각 실린더에 따라 차이가 있지만 RMSE, MSE, MAE는 0.14~2.23의 점수를 나타냈고, R²는 거의 1에 가까운 높은 점수를 나타내었다.

Fig. 10

Performance evaluation of regression model

3.2 연소실 압력의 예측 및 실측값 비교

기계학습 모델을 통해 나타낸 연소실 압력의 예측값과 실측값을 선박 엔진의 부하 구간에 따라 P-T 선도로 나타내어 결과를 비교하였다.

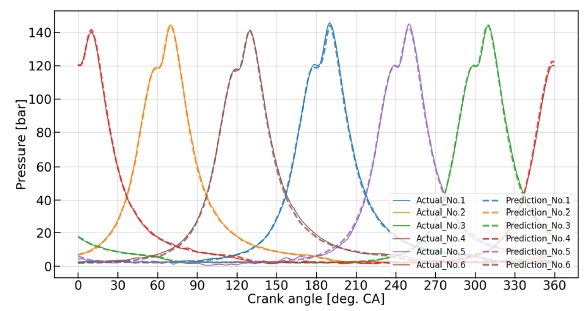
Fig. 11은 엔진 50% 부하의 1 사이클 테스트 데이터를 기계학습 모델에 적용하여 나타난 6개 실린더 연소실 압력의 예측값과 실측값을 각각 점선 및 실선으로 나타내어 비교한 그래프이다.

Fig. 11

P-T diagram comparing predicted and actual pressure

P-T 선도에 나타난 6개 실린더의 흡입․압축․폭발․팽창과정에서 각 연소실 압력의 예측값과 실측값은 높은 일치를 보여 주고 있으며, 일부 실린더의 흡입 행정에서 약간의 오차가 발생하는 것을 확인할 수 있었다. 또한 압축압력 및 최고압력 구간에서 예측값과 실측값이 비교적 잘 일치하는 것을 확인하였다.

3.3 모델의 예측을 통한 엔진출력 비교

1번 실린더를 대상으로 8번의 테스트 회차에서 도시 평균유효압력 및 출력을 식 (9), (10)을 통해 계산하였다.

$\[ \begin{array}{c}IMEP=\frac{\Delta \theta }{V_S}\sum _{n_1}^{n_2} p_{cyl}\frac{dV}{d\theta }\\ V_S\mathrm{:}\mathrm{ }\mathrm{단}\mathrm{일}\mathrm{실}\mathrm{린}\mathrm{더}\mathrm{행}\mathrm{정}\mathrm{체}\mathrm{적}, \theta \mathrm{:}\mathrm{ }\mathrm{크}\mathrm{랭}\mathrm{크}\mathrm{각}\mathrm{도}\mathrm{,} n \mathrm{:}\mathrm{ }\mathrm{적}\mathrm{분}\mathrm{구}\mathrm{간}\mathrm{,}\mathrm{ } p_{cyl}:\mathrm{실}\mathrm{린}\mathrm{더}\mathrm{압}\mathrm{력}\end{array} \]$

(9)

$\[ \mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}=\frac{(IMEP\cdot RPM\cdot V_s)}{7500\cdot 60}\cdot 0.736 \]$

(10)

Fig. 12는 25%, 50%, 70% 부하 구간에서 각각 8 사이클의 테스트 데이터를 대입한 평균 출력 및 오차율을 나타낸 막대그래프이다. 연소실 압력의 실측값과 예측값을 통한 출력의 평균은 약 3% 이하의 오차율을 나타낸 것을 확인하였다.

Fig. 12

Comparison of average power at each engine load

4. 결 론

본 연구는 연소실의 압력변동과 크랭크축 각속도 사이의 상관관계에 착안하여 심층 신경망을 활용한 기계학습 모델을 통해 연소실 압력을 역추적하였다. 취득한 데이터의 전처리 및 최적의 심층 신경망 모델을 통한 연소실 압력의 예측값과 실측값을 비교․분석하여 다음과 같은 결론을 얻었다.

1) 엔진 부하를 기준으로 실린더별 회귀분석 성능지표에서 RMSE, MSE, MAE는 0.14~2.23의 점수를, R²는 1에 근접한 양호한 점수를 보였다. 그리고 P-T 선도에 나타난 연소실 압력의 예측값과 실측값의 비교를 통해 높은 일치를 확인하였다. 따라서 크랭크축 각속도를 활용한 기계학습 모델이 각 실린더의 연소실 압력 센서를 백업 및 대체할 수 있는 가능성을 확인하였다.

2) 연소실 압력의 예측값과 실측값을 적용하여 엔진의 출력을 계산 및 비교하였다. 8 사이클의 테스트 결과 평균 3% 이내의 오차가 발생했고, 이는 크랭크축 각속도의 저주파통과필터의 차단 주파수 설정과 연소실 압력에 사용된 평활화 방법에 따른 것으로 판단된다. 향후 연구는 동일 조건의 선박 상태에서 데이터를 취득하여 신뢰성을 높이고 오차범위를 줄이고자 한다. 이를 달성하기 위해 합성곱 신경망(Convolution Neural Network, CNN) 및 순환 신경망(Recurrent Neural Network, RNN) 알고리즘을 활용한 딥러닝 모델을 비교하여 가장 효과적인 알고리즘을 식별하고 정확도를 높일 수 있을 것으로 기대한다.

3) 본 연구의 기계학습 모델은 연소실 압력 실측값에 근접한 결과를 나타냄으로써 연소실 압력 데이터를 실측하기 어려운 선박용 중소형 엔진의 상태 진단에 큰 도움이 될 것으로 판단된다. 또한 스마트 선박 및 자율주행 선박 시대가 도래함에 따라 본 연구의 기술개발로 고장빈도가 잦은 압력 센서의 백업 역할을 하여 부품교체 비용을 절감하고 연소실 압력을 정확하게 예측할 수 있을 것으로 기대된다.

Acknowledgments

본 연구는 부산광역시 및 (재)부산인재평생교육진흥원의 BB21플러스 사업, 산업통상자원부의 연구비 지원으로 수행된 ‘자율운항선박 기술개발사업((K_G012001614002)’ 및 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다. (No.2021R1G1A1008612) 이에 감사드립니다. 또한 본 논문은 2023년도 김영민 석사학위 논문에서 발췌‧정리하였음을 밝힙니다.

References

• J. Powell, 1993, “Engine control using cylinder pressure: past, present, and future”, Journal of Dynamic Systems, Measurement, and Control, 115(2B), 343-350. [https://doi.org/10.1115/1.2899074]
• V. Rocco, 1993, “DI diesel engine in-cylinder pressure data analysis under TDC setting error”, SAE Technical Paper, (930595), 41-49. [https://doi.org/10.4271/930595]
• J. H. Park, K. H. Choi and S. G. Lee, 2009, “Analysis and Evaluation Study on Diesel Generator Engine Operation Signature”, Journal of Power System Engineering, 13(5), 82-88.
• S. Leonhardt, N. Muller and R. Isermann, 1999, “Methods for engine supervision and control based on cylinder pressure information”, IEEE/ASME Transactions on Mechatronics, 4(3), 235-243. [https://doi.org/10.1109/3516.789682]
• S. Kunifumi, K. Yoshiaki, T. Kita and M. Kenjiro, 1987, “Individual cylinder knock control by detecting cylinder pressure”, SAE Transactions, 96(5), 602-606. [https://doi.org/10.1109/3516.789682]
• W. Xi, Z. Li, Z. Tian and Z. Duan, 2017, “A feature extraction and visualization method for fault detection of marine diesel engines”, Measurement, 116, 429-437. [https://doi.org/10.1016/j.measurement.2017.11.035]
• S. A. Ali and S. Saraswati, 2015, “Cycle-by-cycle estimation of cylinder pressure and indicated torque waveform using crankshaft speed fluctuations”, Transactions of the Institute of Measurement and Control, 37(6), 813-815. [https://doi.org/10.1177/0142331214549093]
• C. Bennett, J. F. Dunne, S. Trimby and D. Richardson, 2017, “Engine cylinder pressure reconstruction using crank kinematics and recurrently-trained neural networks”, Mechanical Systems and Signal Processing, 85, 126-145. [https://doi.org/10.1016/j.ymssp.2016.07.015]
• G. Rizzoni and W. B. Ribbens, 1989, “Crankshaft position measurement for engine testing, control, and diagnosis”, IEEE 39th Vehicular Technology Conference, 423-436. [https://doi.org/10.1109/VETEC.1989.40109]
• S. C. Wang, 2003, “Interdisciplinary Computing in Java Programming”, Springer Science and Business Media, 81-100. [https://doi.org/10.1007/978-1-4615-0377-4_5]
• R. Hecht-Nielsen, 1989, “Theory of the Backpropagation Neural Network”, IEEE International Conference on Neural Network, 1, 593-605. [https://doi.org/10.1109/IJCNN.1989.118638]
• KR, 2014, “Control of Ship Vibration and Noise”, Textbooks, Paju, 367.
• G. S. Jung and J. W. Lee, 2015, “A study on an instantaneous angular velocity and torque fluctuation for marine diesel engine”, Journal of Advanced Marine Engineering and Technology, 39(7), 722-728. [https://doi.org/10.5916/jkosme.2015.39.7.722]
• M. Lapuerta, J. Sanz-Argent and R. Raine, 2014, “Heat release determination in a constant volume combustion chamber from the instantaneous cylinder pressure”, Applied Thermal Engineering, 63(2), 520-527. [https://doi.org/10.1016/j.applthermaleng.2013.11.044]
• A. Géron, 2022, “Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow”, Hanbit Media, Inc., Seoul, 68-122.