The Korean Society for Power System Engineering

[ Article ]

Journal of Power System Engineering - Vol. 27, No. 4, pp.19-25

ISSN: 2713-8429 (Print) 2713-8437 (Online)

Print publication date 31 Aug 2023

Received 17 Feb 2023 Revised 10 Apr 2023 Accepted 11 Apr 2023

DOI: https://doi.org/10.9726/kspse.2023.27.4.019

유도파 모드분리 및 반사계수에 의한 배관 결함검출

박경조^*^{, †}

*교수, 전남대학교 기계설계공학부

Detection of Pipe Defects Using Mode Separation and Reflection Coefficients in Guided Wave Tests

Kyung-Jo Park^*^{, †}

*Professor, Department of Mechanical Design Engineering, Chonnam National University.

Correspondence to: ^†Kyung-Jo Park : Professor, Department of Mechanical Design Engineering, Chonnam National University. E-mail : kjpark40@jnu.ac.kr, Tel : 061-659-7221

초록

이 논문에서는 비틀림 유도파 T(0,1) 모드가 원주방향 결함에서 반사될 때 나타나는 상호작용에 대해 정량적인 연구를 수행한다. 첩릿변환을 이용하여 결함에서 반사된 다중 모드 신호를 분리하여 추출하는 방법에 대해 기술한다. 분리된 모드를 이용하여 반사계수를 계산할 수 있고 이를 통해 결함의 정량적 해석이 가능하다. 강관에 대한 시뮬레이션 예제를 통해 제안된 방법의 타당성을 검증하고 그 효용성을 입증한다. 연구 결과, 결함 길이가 증가함에 따라 반사계수가 선형으로 증가하는 것을 확인할 수 있고 이로부터 제안된 방법을 이용하여 결함 특성을 정량적으로 규명할 수 있음을 보인다.

Abstract

A quantitative study of the interaction of the T(0,1) torsional mode with circumferential defects in a pipe is presented in this paper. A mode decomposition technique employing the chirplet transform is used to separate the multi-modal signals reflected from the defects. Reflection signals are obtained from simulation results on a carbon steel pipe. The influence of the crack length is investigated. The results show that the reflection coefficients are linearly dependent on the circumferential extent of the defects, which show the accurate and quantitative defect characterization could become enabled using the proposed technique.

Keywords:

Guided Waves, Mode Separation, Reflection Coefficients, Defect Detection, Chirplet Transform

키워드:

유도초음파, 모드 분리, 반사계수, 결함검출, 첩릿변환

1. 서 론

초음속 유도파(ultrasonic guided wave)검사를 이용하여 석유화학 배관의 내부 상태를 검사하는 방법이 최근 활발히 적용되고 있으며 기술적 발전도 비약적으로 이루어지고 있다.^1,2) 결함의 형상은 비축대칭이므로 모드 변환에 의해 비축대칭 모드인 휨모드(flexural mode)가 발생한다. 이러한 모드변환은 입사 모드와 모드 변환된 모드의 입자운동이 유사할 때 쉽게 발생하는데, 모드변환에 의해 발생하는 휨파의 경우 분산성(dispersion)을 가지며 군속도(group velocity)가 입사 모드의 군속도와 매우 근접해 있다. 이러한 특성 때문에 유도파를 배관검사에 적용하는데 어려움이 있다. 일반적으로 모드의 분산성이 심하면 시간 신호가 길게 펼쳐지게 되고, 모드의 진폭이 작아지며 심지어 서로 다른 모드끼리 중첩되는 현상이 나타난다. 이러한 특성 때문에 공간과 시간영역에서 분해능(resolution)이 낮아지게 되고 수신기에서 모드를 탐지할 수 있는 능력도 약해지게 된다.³⁾

분산성을 갖는 신호를 분석하는 방법으로 널리 사용되고 있는 것이 STFT(Short Time Fourier Transform)와 웨이브렛변환(wavelet transform) 기법이다.⁴⁾ 그러나 이 방법들은 유도파 모드 중 휨파에 의한 분산성을 분석하기 어려운 단점이 있어 좀 더 정밀한 신호처리를 수행할 수 방법들이 개발되어 왔는데, 유도파 분산성에 기반한 STFT⁵⁾, 정합추적(matching pursuit),⁶⁾ 왜곡 주파수변환(warped frequency transform)⁷⁾ 등을 예로 들 수 있다.

그러나 이 방법들을 이용하여 모드를 분리하기 위해서는 복잡한 다채널 자료획득 및 처리를 위한 장비들이 필요한 단점이 있다. 이에 대한 대안으로 첩릿변환(chirplet transform)을 활용할 수 있는데, 이를 이용하여 특정한 순간 주파수와 군속도를 갖는 신호에서 개별 모드 성분을 추출할 수 있다. 추출된 개별 모드를 이용하여 반사계수(reflection coefficient)를 계산할 수 있고 각 모드들의 반사계수를 비교하여 결함의 크기를 정량적으로 판별할 수 있다.

이 논문에서는 최대가능추정방법에 의한 첩릿 변환을 소개하고 이를 이용하여 모드를 분리하고자 한다. 상용 프로그램을 이용하여 결함에서 반사된 신호를 획득하고 개발된 첩릿변환 알고리즘을 시뮬레이션 신호에 적용하여 분산성을 갖는 신호로부터 모드를 분리하고, 각 모드들의 반사계수를 계산한다. 그리고 원주방향 길이의 변화에 따른 각 모드들의 반사계수 변화로부터 결함의 크기를 정량적으로 정확하게 판별할 수 있음을 보인다.

2. 첩릿변환과 응용

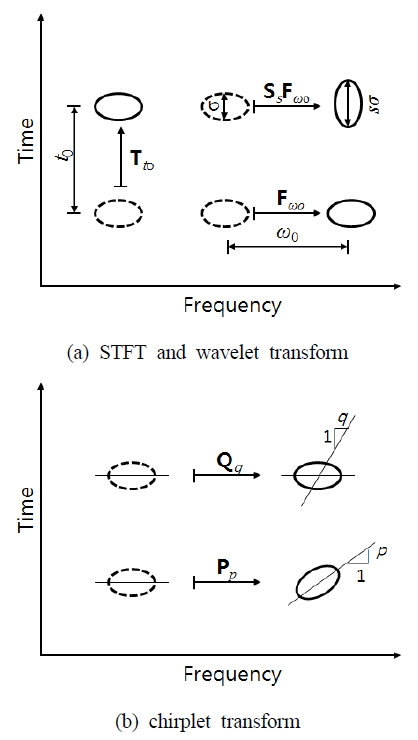
첩릿변환은 STFT기법과 웨이브렛기법의 장점을 모두 채택한 방법으로 Mann과 Haykin에 의해 소개되었다.⁸⁾ 기저함수(basis function)는 천이(shift), 전단(shear), 확대(scaling) 연산자에 의해 조절이 가능하며, 따라서 에너지밀도를 5차원의 매개변수 공간으로 표현한다. 이에 대한 비교는 Fig. 1에 자세히 표시하였다. 다섯 개의 기저함수(시간천이, 주파수천이, 확대, 주파수전단, 시간전단)에 의한 변환 결과는 Table 1에서 비교․정리하였다.

Fig. 1

Representation of time-frequency atoms

Table 1

Operations for time-frequency atoms for the chirplet transform

첩릿변환에 사용되는 첩릿은 다음 식에 의해 정의된다.

C c t t o, ω o, s, p, q = ∫ - ∞ ∞ x t g t o, ω o, s, q, p * t d t = 1 2 π ∫ - ∞ ∞ X ω G t o, ω 0, s, q, p * ω d ω

(1)

여기서, t_o, ω_o, s, q, p는 각각 시간, 주파수, 확대율, 첩변화율, 지속시간을 나타낸다. 첩릿변환의 후리에 변환 G(ω)는 식 (2)와 같이 첩신호 군에 속해 있다.

G t o, ω o, s, p, q (ω) = T t o F ω o S s Q q P p H (ω) q t o, ω o, s, p, q (t) = T t o F ω o S s Q q P p h (t)

(2)

여기서, T_{t_o}, F_{ω_o}, S_s, Q_q, P_p는 Table 1과 같은 연산을 수행하는 연산자들이다. 측정된 신호를 식 (3)의 에너지 분포를 갖는 첩릿 신호로 변환하는 것이 첩릿변환의 최종 목표이다.

P c t t o, ω o, s, p, q = C c t t o, ω o, s, p, q 2

(3)

이를 위해 최대가능추정(maximum likelihood estimate) 방법을 사용한다. O’neill은 가중치를 갖는 Gabor함수로 유도파 신호를 분해하였는데, 이 방법은 정합추적(matching pursuit)에서 사용한 기저함수와 비슷한 형태로 신호를 희소근소화(sparse representation) 방법으로 표현할 수 있다.⁹⁾ 그러나 정합추적에서 사용하는 함수는 유한개의 후보군에서 선정하는 반면 첩릿변환에서는 무한개의 사전에서 선택하기 때문에 분산성을 갖는 파동을 좀 더 정확하게 묘사할 수 있는 장점을 갖는다. 그러나 이 방법은 계산시간이 많이 소요되는 단점이 있으므로 이를 개선하기 위해 다음과 같은 최적화 방법을 제시한다. 그 순서는 다음과 같다.

먼저 모호성함수(ambiguity function)을 이용하여 첩변화율과 지속시간을 추정한다. 그리고 두 기저함수의 추정값을 이용하여 다른 매개변수(시간, 주파수 위치)를 예측한다. 세 번째로 시간, 주파수 위치를 이용하여 국부적으로 첩변화율과 지속시간을 다시 추정한다.

마지막으로 준-뉴톤 방법을 이용하여 주어진 수렴조건을 만족할 때까지 두 번째, 세 번째 단계를 반복한다.

3. 모드분리

첩릿변환을 이용한 모드분리 방법의 타당성을 검증하기 위해 길이 1 m, 반경 12.7 mm, 두께 1.6 mm 배관에 대한 시뮬레이션을 수행하였다. 유도파 검사를 수행하기 위해서는 먼저 분산선도(disperse diagram) 예측이 필수적인데, 이를 위해 Disperse^®라는 사용 프로그램을 사용하였다. 위상속도(phase velocity)와 군속도(group velocity)에 대한 분산선도를 Fig. 2에 제시하였는데, 먼저 T(0,1) 모드의 위상속도, 군속도는 모든 주파수에서 동일한 값(3,420 km/s)을 갖는다는 것을 알 수 있다. 전주파수 영역에서 속도가 일정한 유도파는 비분산성을 갖는다는 것은 잘 알려진 사실로 이 모드를 가진 모드로 선정하면 순수 축대칭 모드 가진이 가능하다는 것을 알 수 있다. 시뮬레이션의 입사파의 주파수는 128 kHz로 선정하였는데, 이 주파수에서는 F(1,2), F(2,2) 모드의 분산성이 다른 주파수대역에 비해 상대적으로 작기 때문이다.

Fig. 2

Dispersion curves for a 25.4 mm bore pipe

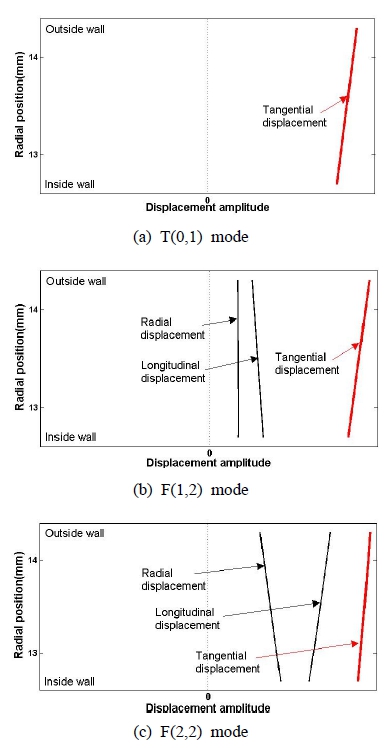
배관에 결함이나 지지대와 같은 불연속 구조물이 없을 경우 축대칭파를 입사하면 대칭 모드만 유도파 신호변환기에 측정된다. 그러나 결함이 존재하면 축대칭파가 휨파와 같은 비축대칭파로 모드변환되고, 이는 두 파의 변위 형태가 유사하면 그 가능성이 훨씬 증가한다. 세 모드의 변위 모드를 Fig. 3에 제시하였는데, 세 모드 모두 접선방향 변위(tangential displacement)가 가장 주요하게 나타나는 것을 알 수 있고 이로부터 T(0,1)모드가 휨파로 변환될 가능성이 큰 것을 알 수 있다. 비틀림파와 달리 F(1,2), F(2,2)모드는 축방향, 반경방향 변위도 나타나는데, 이러한 운동 방향에 의해 분산성이 더 증가되게 된다.

Fig. 3

Displacement mode shapes at 128 kHz

모의시험에 사용된 입사 모드를 Fig. 4에 나타내었다. 순수한 10 사이클, 128 kHz 비틀림 모드 T(0,1)이 가진된 경우로 분산성이 없는 것을 확인할 수 있다. 대상 배관의 중간 지점(배관 끝단에서 0.5 m)에 결함이 존재할 경우 신호변환기에 측정된 반사신호는 Fig. 4(b)와 같이 나타난다. 결과는 배관 끝단에서 반사된 신호의 크기에 대해 정규화하여 나타내었다. 입사파는 하나의 단일한 모드로 구성되어 있지만, 결함에서 반사된 신호는 여러 개의 모드가 동시에 나타나는 것을 알 수 있다. 각 모드들의 진폭은 첫 번째 모드가 가장 크고 점차 줄어드는 것을 알 수 있으며, 모드 사이의 간격도 동일하지 않은 것을 알 수 있다. 즉 결함에 의해 모드변환된 신호들이 나타나고, 다중 모드에는 축대칭 모드와 비축대칭 모드가 혼재되어 있는 것을 확인할 수 있다. 또한 각 모드들의 분산성도 다르게 나타나는 것을 알 수 있다.

Fig. 4

Input and reflection signals after 1 m propagation

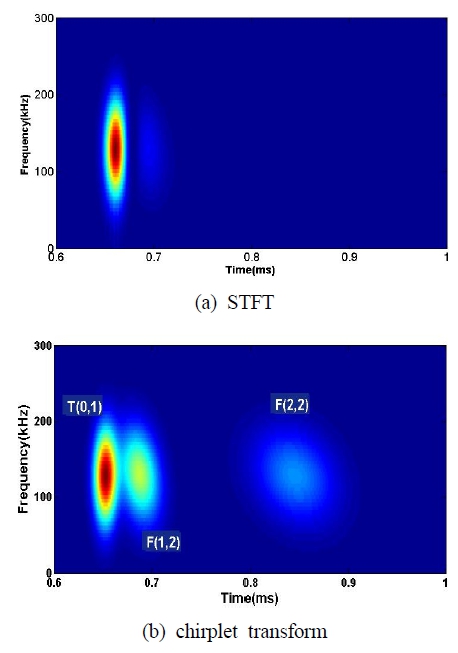
결함에서 반사된 신호에만 두 가지 신호처리 기법을 적용하여 그 결과를 시간-주파수 영역에서 나타낸 것이 Fig. 5에 제시되어 있다. STFT와 첩릿변환 모두 축대칭파인 T(0,1) 모드는 정확하게찾아내지만, STFT는 분산성이 큰 비축대칭 모드는 찾아내지 못하는 것을 알 수 있다. 반면 첩릿변환은 다섯 개의 기저 함수를 모두 추적하여 신호를 분석하기 때문에 에너지 성분이 상대적으로 적은 휨파도 시간, 주파수 위치뿐만 아니라 변화율까지 정확하게 분석할 수 있음을 알 수 있다.

Fig. 5

Spectrogram of the signal in figure 4(b)

첩릿변환을 통하여 분리한 반사 신호의 개별 성분들을 Fig. 6에 제시하였다. 반사 신호에 포함된 각 모드들의 진폭과 반사시간(결함위치)를 정확하게 예측하고 있음을 알 수 있는데. 결함위치는 분산선도에서 예측한 군속도에 반사 시간을 곱하면 쉽게 계산할 수 있다. Fig. 6(c)에 제시된 F(2,2)모드의 진폭이 T(0,1) 모드의 8%에 불과하고, 중심 주파수 위치도 입사파에 비해 3 kHz 이동하였으며, 분산성을 나타내는 첩변화율과 지속 시간이 크게 증가하였음을 알 수 있다.

Fig. 6

Separated wave forms using the chirplet transform

첩릿변환에 의해 분리된 모드를 이용하여 입사 주파수 128 kHz에서 구한 각 모드의 반사계수를 Fig. 7에 나타내었다. 그림에서 가로축은 배관 전체 원주에 대한 결함의 원주 방향 길이 비를 나타낸 것으로 결함 길이가 100%이면 완전 관통된 상태를 나타낸다. 세로축은 입사 모드의 진폭에 대해 반사 모드의 진폭을 비율로 표시한 반사계수이다. 축대칭파인 T(0,1) 모드의 반사계수는 결함 길이가 증가할수록 비례하여 커지는 것을 알 수 있다.

Fig. 7

Reflection coefficients for a half wall thickness notch at 128 kHz

즉 결함 크기에 따라 T(0,1) 모드크기도 증가하므로 결함의 크기 판별에 유용한 정보를 제공한다. F(1,2), F(2,2) 모드의 반사계수는 반정현파(half-sine)와 정현파형태를 갖는다. 즉 F(1,2) 모드의 경우 결함 길이가 원주의 1/2일 때 가장 큰 진폭을 갖는다는 것을 확인할 수 있다. 다른 모드에 비해 반사계수가 가장 적게 나타나는 F(2,2) 모드는 원주의 25, 75% 부근에서 반사계수가 최고값을 갖고 결함 크기가 원주의 50%일 때는 반사계수가 거의 0이 되어(반사계수 0.001) 반사 신호에 거의 나타나지 않음을 알 수 있다. 이로부터 첩릿변환을 이용하여 모드를 분리하여 각 모드들의 반사계수를 구하면 결함의 위치뿐만 아니라 크기까지 정확하게 예측할 수 있음을 알 수 있다.

4. 결 론

배관의 축대칭 파동인 T(0,1) 모드를 이용하여 원주방향 결함에서 반사되는 반사 신호의 특성을 파악하는 방법을 개발하였다. 개발된 방법은 첩릿변환애 기초하여 다중 모드를 분리하고, 분리된 모드들의 반사계수를 계산하여 결함의 위치 및 크기를 파악하는 방법으로, 기존의 신호처리 기법에 비해 첩변화율과 지속시간을 정확하게 예측할 수 있어 분산선이 큰 유도파 신호의 해석에 매우 유리한 장점을 갖고 있다.

개발된 알고리즘은 무한대의 함수 사전을 이용하는 방법으로 기존의 신호처리 기법으로는 파악이 어려운 휨파 모드의 탐지 및 분리가 가능한 방법이다. 따라서 기존 신호처리 기법에 비해 분해능이 우수하고 분산성이 심한 다중 모드를 개별 모드로 정확하게 분리할 수 있으므로 유도파 시험에서 결함의 정량적 크기 파악에 유용하게 사용될 수 있을 것으로 판단된다.

Author contributions

K. J. Park; Conceptualization, Analysis, Simulation, Methodology, Writing-original draft and review, Editing.

References

A. Demma, P. Cawley, M. Lowe, A. G. Roosenbrand and B. N. Pavlakovic, 2004, “The reflection of guided waves from notches in pipes: a guide for interpreting corrosion measurements”, NDT&E International, 37(1), 167-180. [https://doi.org/10.1016/j.ndteint.2003.09.004]
R. Carandente and P. Cawley, 2012, “The effect of complex defect profiles on the reflection of the fundamental torsional mode in pipes”, NDT&E International, 46(3), 41-47. [https://doi.org/10.1016/j.ndteint.2011.11.003]
K. J. Park, 2022, “Characterization of symmetric reflection modes and detection of defect in pipelines”, Journal of Korean Society for Power System Engineering, 26(5), 30-37. [https://doi.org/10.9726/kspse.2022.26.5.030]
W. H. Prosser, M. D. Seale and B. T. Smith, 1999, “Time-frequency analysis of the dispersion of Lamb modes”, Journal of Acoustical Society of America, 105(3), 2669-2676. [https://doi.org/10.1121/1.426883]
J. C. Hong, K. H. Sun and Y. Y. Kim, 2005, “Dispersion-based short-time Fourier transform applied to diseprsive analysis”, Journal of Acoustical Society of America, 117(5), 2949-2960. [https://doi.org/10.1121/1.1893265]
G. L. Touze, B. Nicolas and J. I. Mars, 2009, “Matched representations and filters for guided waves”, IEEE Transactions on Signal Processing, 57(6), 1775-1783. [https://doi.org/10.1109/TSP.2009.2013907]
L. D. Marchi, K. Xu and N. Speciale, 2009, “Ultrasonic guided-waves characterization with wrapped frequency transforms”, Proceedings of IEEE. [https://doi.org/10.1109/ULTSYM.2008.0046]
S. Mann and S. Haykin, 1995, “The chirplet transform: physical considerations”, IEEE Transactions on Signal Processing, 43(2), 2745-2761. [https://doi.org/10.1109/78.482123]
J. C. O’neill and P. Flandrin, 2000, “Sparse representations with chirplets via maximum likelihood estimation”, IEEE Transactions on Signal Processing, 40(2),1842-1853.