동적 변분-점근적 과정을 통한 최적의 빔 이론
Abstract
Unlike most published work on beam modeling only suitable for the low-frequency and long-wavelength approximation, the present research proposes new development procedures to rigorously construct an accurate model for the dynamics of beams over a wide range frequencies and wavelengths. To do this, a dimensional-reduction yielding a beam theory with the aid of small parameters that are inherent to the beam problem is carried out using dynamic variational-asymptotic method to derive one-dimensional equations within low-frequency and long-wavelength regime. In addition, construction of a dynamic beam theory must involve another dimensional-reduction procedure for the high-frequency behavior as well as a separate and logically independent step for the short-wavelength regime. As a direct outgrowth of the present theory, a computer code is developed and provided to represent dispersion curves depending on various degrees of freedom and allow the selection of the optimal variables for approximate beam model through comparison with the three-dimensional finite element method. The excellent agreement demonstrates the capabilities of the present model to analyze dynamic structural responses over a wide range of frequencies and wavelengths
Keywords:
Dimension-reduction method, Dynamic variational-asymptotic method, Dispersion curve1. 서 론
빔 구조란 기하학적 관점으로 한 차원의 길이가 다른 두 차원의 길이들보다 매우 큰 3차원 구조를 말한다. 이러한 구조는 기계, 항공우주, 건설 등 여러 산업분야에서 다양하게 활용되고 있으며, 지속적으로 공학적 관심을 받아왔다.
그런 까닭으로 임의의 정적 및 동적 외부 하중에 의한 빔 구조의 독특한 거동들을 정확하고 효율적으로 분석하기 위해, 지금까지도 광범위한 구조 해석학적 연구들1)이 이루어지고 있다. 특히 고성능 컴퓨터의 발달과 함께 구조의 기하학적 및 재료학적인 면들을 모두 고려한 3차원 유한요소법(FEM: Finite element method)이 통상적인 구조 해석방식으로 채택되어 왔다. 이 방식으로부터 높은 정확도의 해석결과들이 계산되지만, 그 과정에서 야기되는 수치해석상의 과도한 시간과 부하는 이 해석 적용범위를 장파장 및 저주파수내 영역으로 한정시켜 버렸다. 따라서 기존의 3차원 FEM의 대안으로서 광범위한 구조의 동적거동을 다룰 수 있는 새로운 해석방식이 시급하게 요구되어 왔다.
특히 새로운 해석방식의 개발과정에서, 빔 구조의 종횡비와 변형률 모두가 충분히 작다고 가정함으로써, 일반적인 3차원 구조 해석을 기반으로 한 모델링이 아닌 차원-감소법(Dimensional-reduction method)을 통한 1차원 기반의 모델링이 도입되었다. 이러한 시도는 다양한 빔 이론으로 명명되어 많은 문헌들2)을 통해 지속적으로 소개되고 있다. 하지만 소개된 대다수의 빔 이론들은 암시적으로 정역학적 관점인 장파장 및 저주파수 가정아래에서 개발되었고, 그 외 범위에서는 개발된 이론 내 자체적인 확장성 및 체계성의 결여로 인해 1차원적 빔 모델링의 효율성 및 정확성의 한계점들이 여러 문헌들3,4)을 통해 보고되었다.
내포된 가정으로부터 야기되는 이론적 제한성을 제거하기 위해, 본 논문은 동적 변분-점근법(Dynamic variational-asymptotic method)5,6)을 기반으로 한 새로운 빔 이론의 개발 과정을 소개하고, 이 방법론을 검증하고자 한다. 또한 기존의 통용되는 두 빔 이론들 ― 4개 자유도를 바탕으로 한 고전 빔 이론과 6개 자유도를 바탕으로 한 티모센코(Timoskenko) 빔 이론 ― 을 개발된 이론으로부터 체계적으로 유도되는 과정을 보여준다. 그리고 선별된 10개의 자유도(Degree of Freedom)를 기반으로 한 최적의 빔 이론을 처음으로 소개함으로서 본 이론의 확장성과 체계성을 검증하고자 한다. 이 모든 과정을 명확히 예증하기 위해, 중실 단면적 균질 등방성 빔 구조가 사용됐고, 특히 3차원 FEM와 빔 이론들로 구현된 분산곡선들 간에 세부적으로 비교함으로써 본 이론의 정확성과 효율성을 검증하고자 한다.
2. 동적 변분-점근법
2.1 3차원 빔 기하학
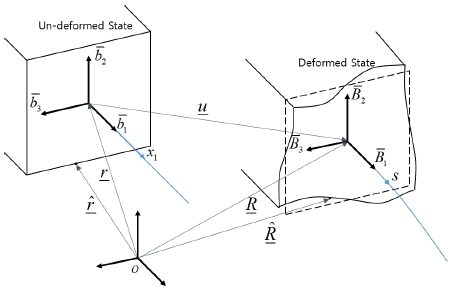
우선 임의의 외부하중에 의한 빔의 변형 전과후의 형상들을 기하학적으로 표현하기 위해, 관련된 각 빔 단면적(C-S: Cross-section)의 기준선에 수직한 직교 프레임(frame)들과 이들을 구성하는 방향 단위벡터들인 bi와 Bi가 Fig. 1과 같이 사용된다. (본 논문 내에서 아래첨자 α는 2와 3을 의미하고, 아래첨자 i와 j는 1, 2와 3을 나타낸다.) 그러므로 변형 전과 변형 후 질점에 대한 3차원 위치벡터들은 다음과 같이 정의된다.
| (1) |
| (2) |
여기서 r과 R = r + u은 변형 전과 후의 기준선상의 점에 대한 위치벡터이며, u = uib1은 1차원 변위벡터를 나타낸다. 그리고 wi는 R와 Bi 이외 임의의 빔 변형들을 나타내는 미지의 3차원 변동함수이다. 또한 두 방향 단위벡터들의 관계식은 관련된 프레임들 간의 회전을 나타내는 방향 코사인 행렬(CBb)으로서 수식화가 이루어진다.
| (3) |
특히, 변동함수 내 빔 강체(rigid body)거동에 대한 영향이 배제되고 과 (R, Bi, wi) 간의 고유한 일대일 관계식이 유지되기 위해 네 가지 구속조건들이 식 (2)로부터 정의된다.
| (4) |
| (5) |
여기서, < >은 단면적으로 정적분하는 것을 의미한다.
다음으로 확장된 해밀턴(Hamilton)이론을 활용하여 임의의 3차원 빔 거동을 해석하기 위해서는 3차원 변형률 장(Γij)과 속도 장()이 1차원 고전 변형률() 및 곡률()와 고전 선속도() 및 각속도()로 표현되어야 한다.
| (6) |
| (7) |
여기서, Γ = [Γ11 2Γ12 2Γ13 Γ22 2Γ23 Γ33]T,
, ( )ʹ = ∂()/∂x1, (ㆍ) = ∂()/∂t, Δ3와 O3은 3 × 3 단위행렬과 영행렬을 나타낸다. 그리고 식 (6)과 (7)에서 소개된 연산자들은 다음과 같이 표현된다.
| (8) |
2.2 변분-점근법을 통한 확장된 해밀턴 이론
3차원 빔 구조의 정적 및 동적 거동을 분석하기 위해 확장된 해밀턴 이론의 변분식2)이 주로 사용된다. 또한 식 (2)내 미지의 3차원 변동함수가 확장된 해밀턴 이론을 통해 계산되어질 때, 일반적인 수치해석 기법이 직접적으로 이 과정에서 구현되어질 수 있다. 하지만 이런 방식은 기존의 3차원 탄성동역학 문제를 3차원 FEM으로 구현하는 것과 동일하게 과도한 전산 비용 및 시간의 문제들을 야기시킨다. 따라서 수치해석상에 발생할 수 있는 문제들을 해결하기 위해, 변분-점근법2)을 활용한 차원-감소 과정이 확장된 해밀턴 이론에 도입된다. 여기서 이와 같은 과정이 가능한 이유는 통상적으로 공학용 빔 구조의 종횡비와 변형률 모두 충분히 작다는 사실을 근거로 하고 있기 때문이다.
변분-점근법이란 빔 구조 내 역학적 및 기하학적 고유변수의 미소성(infinitesimal)을 기반으로 한 차원-감소 과정으로 3차원 탄성학 문제를 비선형 1차원 빔 문제와 선형 2차원 단면적 문제로 나누어 병렬적으로 해석하는 방식이다. 이러한 방식은 3차원 FEM기반의 직접적인 해석 방식의 대안으로서, 여러 문헌들2,4)을 통해 높은 수준의 정확성과 효율성이 검증되었다. 따라서 확장된 해밀턴 이론의 3차원 변분식에 변분-점근법을 수행함으로서, 다음과 같은 빔의 1차원 에너지 범함수로 재구성되어진다.
| (9) |
여기서, t1과 t2는 고정된 임의의 시간을 의미하고, l은 빔의 전체 길이이며, δW는 다양한 외부 하중의 영향으로 발생된 에너지를 수식화한 가상일을 나타낸다. 그리고 라그랑지안(Lagrangian)인 L은 단위 길이 당 운동에너지 밀도와 탄성에너지 밀도의 차로 정의된다.
| (10) |
또한 K와 U는 식 (6)과 (7)을 사용하여 간결하게 행렬 형식으로 정의된다.
| (11) |
| (12) |
여기서, ρ는 질량밀도, D는 6 × 6 재료상수 행렬이다.
비록 식 (9)는 3차원 해석방식의 대안으로 사용함으로써 이론의 효율성이 증대되지만, 식 (9)로 주어진 비선형 1차원 빔 문제를 해결하기 위해, 선형 2차원 빔 단면적 해석이 우선적으로 수행되어야 한다. 이때 이론의 고범용성을 위한 2차원 FEM의 전산화 기법이 본 이론의 개발과정에서 도입되어지고, 이는 3차원 변동함수를 다음과 같이 변수분리화 함으로써 구현되어진다.
| (13) |
여기서, S는 형상함수이고, W는 단면적의 변동에 대한 절점 값인 함수이다.
식 (13)를 식 (11), (12)에 대입함으로써, 운동에너지와 탄성에너지는 전산화에 용이한 형태로 구해진다.
| (14) |
| (15) |
여기서, 무차원 변수인 ζα = h-1xα가 사용되었고, , Dtv = <S>, ,
H = <STS>, E = <[ΓhS]TD[ΓhS]>,
Dhε = <[ΓhS]TD[Γε]>,
Dhl = <[ΓhS]TD[Γε]>,
Dεε = <[Γε]TD[Γε]>, Dlε = <[ΓlS]TD[Γε]>,
Dll = <[ΓlS]TD[ΓlS]> 이다.
2.3 동적 변분-점근법을 통한 장파장내 저주파 및 고주파 진동 근사과정
본 이론은 다양한 주파수의 진동영역아래 점근적인 차원감소과정을 구현하기 위해, 정역학적인 공간척도의 오더(order)만 고려한 기존의 변분-점근법과는 달리, 동역학적인 시간척도의 오더 또한 함께 다루고 있다. 즉 동적 변분-점근법이란 장파장내 저주파(LF: Low frequency)와 고주파(HF: High frequency) 진동영역을 다음과 같은 시간척도들로 정의하고, 각 영역에 대하여 이를 선별적으로 고려함으로써 변분-점근법이 수행되는 방법을 의미한다.
| (16) |
| (17) |
여기서, cs는 전단파의 속도를 나타내며, τ는 시간오더로서 임의의 시간 내 구조변형에 대한 변화크기를 의미한다.
먼저 장파장내 저주파 진동에 대한 근사 과정을 위해 식 (16)의 시간척도 오더를 고려하자. 그러면 기존의 변분-점근법4,5,7)으로부터 계산되어진 결과와 동일한 오일러(Euler) 방정식과 무차원 해를 도출하게 된다.
| (18) |
| (19) |
여기서, λ는 라그랑주 승수(Lagrange multiplier)이다. 그리고 이며 ( )+는 유사역행렬(pseudo inverse)을 나타낸다. 추가적으로 Φcl은 앞서 소개된 빔 구속조건에 해당하는 3N × 4 행렬 (여기서 N은 단면적의 절점의 개수를 나타낸다.)이며 E에 의해 다음과 같이 정의된다.
| (20) |
반면에 식 (17)의 시간척도 오더는 장파장내 고주파 진동에 대한 근사과정을 수행하게 된다. 이러한 근사과정은 본 문제를 2차원 평면 문제로 가정한 Le의 연구8)가 이미 이루어졌지만, 3차원 빔 문제 그 자체를 다룬 연구는 아직까지도 문헌들 내에서 찾기 어렵다. 따라서 본 연구는 어떠한 공간적 가정 없이 3차원 문제 그 자체로 다루고자 한다.
먼저 식 (17)의 관계식을 식 (14)과 (15)에 대입하고 정의된 오더의 척도로 주요한 항들을 선별하게 된다. 그러면 0차 근사과정으로서 기존의 3차원 빔 문제는 빔 단면적에 대한 고유치문제로 전환되고 다음과 같은 0차 근사해가 구해진다.
| (21) |
식 (21)에서 Λ은 3N × 3N 고유값인 고유진동수의 대각행렬이고 Φ은 진동수에 대한 모드형상들을 나타내는 고유벡터의 3N × 3N 행렬이다. 그리고 는 고유벡터의 모드형상과 연관된 3N × 1 열행렬을 의미한다. 또한 이후 빔 진동해석을 용이하게 위해, W0은 Φ내 고유벡터들 간의 직교성 및 면외 방향(out-of-plane)과 면내 방향(in-plane) 빔 진동들 간의 연관을 고려한 개별적인 진동분기(vibration branch)로서 다음과 같이 정의되어진다.
| (22) |
여기서, 면외 및 면내 방향 진동들을 구분하기 위해 새로운 첨자 d와 k가 소개되어지며, 특히, k는 d에 따른 모드형상의 순서를 나타낸다.
| (23) |
동적 변분-점근과정의 다음단계인 1차 근사과정을 수행하기 위해, 새로운 미지 함수인 가 개별적인 진동분기인 변동함수(W0)에 점근적으로 소개되어진다.
| (24) |
다음으로 식 (24)와 식 (17)을 활용하여, 미지의 변동함수에 관련된 주요 항들로 이루어진 아래의 식이 구해진다.
| (25) |
여기서, , , λ는 라그랑주 승수이다. 그리고 앞선 소개된 0차 근사과정을 동일하게 수행하면, 변동함수는 다음과 같이 와의 선형적인 관계식으로 계산되어진다.
| (26) |
여기서, 이다.
2.4 쌍곡 단파 외삽법화된 에너지 범함수
수학적 관점으로 식 (22)와 (26)을 이용함으로 고주파 에너지 범함수가 정확히 계산되어지지만, 매우 특별한 경우 이러한 변동함수들은 빔 구조 에너지의 양한정성(positive definiteness)을 무효화라는 심각한 역학적 오류를 야기시킬 수 있다. 그러므로 본 이론에서 유도된 빔의 1차원 에너지 범함수가 항상 양한정성을 유지하기 위해, 쌍곡 단파 외삽법(hyperbolic short-wave extrapolation)4)이 다음과 같이 수행되어진다. 먼저 광범위한 주파수내 빔 구조의 동적 거동을 해석하기 위해, n개 진동분기의 자유도(4개 저주파 자유도와 p + q개 고주파 자유도)로 이루어진 에너지 범함수가 연관된 저주파 및 고주파의 변동함수들과 함께 계산된다. 그리고 이러한 함수 내 발생하는 저주파 및 고주파의 교차된 항들은 쌍곡 단파 외삽법의 변수 치환을 통해 다음과 같은 양한정성인 라그랑지안으로 정의된다.
| (27) |
여기서 ,
,
,
,
,
,
,
,
와 같은 표현들이 사용되어진다.
또한 기존의 에너지 범함수와 쌍곡 단파 외삽법이 작용된 에너지 범함수를 구별하기 위해 다음과 같은 기호가 식 (27)에 도입되었다.
최종적으로 식 (27)을 식 (9)에 대입한 후 변분 원리가 적용되어지면 광범위한 진동영역을 다룰 수 있는 1차원 빔 운동방정식이 도출되어진다. 특히 주파수와 파수의 변수로 이루어진 해 zm = cmei(κξ - ϑτ)을 가정하여 결과식에 대입하면, 동적 빔 거동의 고유 특성을 나타내는 1차원 분산관계식이 계산되어진다. 여기서 zm은 임의의 1차원 변수를 나타내며. cm은 해당 변수의 임의의 상수를 나타낸다. (상수 m을 통해 각각의 1차원 변수를 구분한다; m ≤ n) 그리고 κ는 무차원 파수이고 ϑ는 무차원 주파수이다.
3. 수치해석 결과
지금까지 소개된 전 과정은 유한요소법을 기반으로 한 DVABS(Dynamic Variational Asymptotic Beam Sectional analysis)로 전산화 되었다. 이를 통해 임의의 빔 단면적에 대한 면내 및 면외 방향 모드형상들이 범용적으로 계산되어진다. 또한 이러한 모드형상들로부터 DVABS는 선별적으로 선택하여 빔 모델의 개발과정을 자동적으로 수행하게 한다. 동시에 DVABS는 빔 구조의 다양한 동적거동의 특성들을 용이하게 해석하고 근사이론의 타당성을 판단하는 하나의 도구인 분산곡선을 가시화한다. 본 이론의 효율성과 정확성을 검증하기위해, 물성치 E = 2.6 × 108, ν = 0.3을 가지는 가로 세로 각 1 m의 정사각형 중실(Solid) 단면적 등방성 균질 빔 구조가 수치해석적 예제로써 사용되었다. (수식에 무차원화를 적용함에 따라, 그 외의 물성치는 다루지 않음)
3.1 저주파 및 고주파 진동 모드형상들
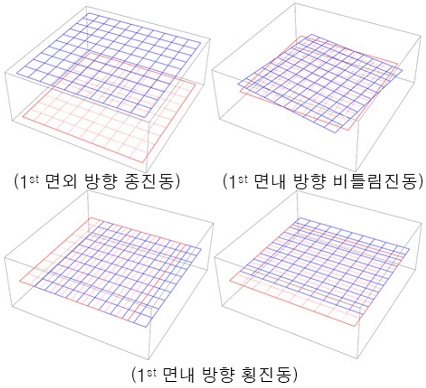
임의의 자유도를 기반으로 한 빔 모델을 소개하기 전에 먼저 이를 구성하는 각 자유도와 빔 변형의 관련성을 보여주고자 한다. 이를 통한 논리적 접근은 기존연구5,6,7)와 차별화되는 부분으로 빔 진동 모드형상을 가시화함으로써 쉽게 검증되며, DVABS를 통해 다양한 빔의 고유진동수와 이와 연관된 모드형상들이 구현된다. 붉은색 점선은 변형 전 단면적을 나타내며 반면에 파란색 실선은 DVABS로 계산되어진 모드형상을 나타낸다.)
Fig. 2는 고전 빔 이론의 4개의 제로인 고유진동수에 대한 모드형상들을 나타내고 있다. 이들은 각각 강체의 인장(1st 면외 방향 종진동), 굽힘(1st 면내방향 횡진동) 그리고 비틀림(1st 면내 비틀림진동) 거동들로 구성된 저주파 진동을 의미한다.
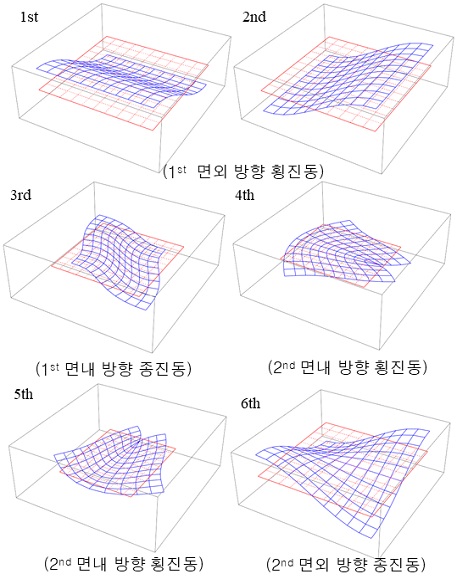
다음으로는 고주파 진동을 나타내는 단면적 진동의 모드형상은 Fig. 3에 보이는 바와 같다. (각모드형상의 왼쪽 상단은 모드형상의 순서를 나타내고, 아래에는 각 모드형상의 진동분기를 나타내었다.) 그림에서 나타난 모드형상 이후로도 많은 모드 형상이 존재하지만, 본 논문의 관심사항이 아니므로 고유진동수의 값 크기순으로 6개의 고주파 진동 모드형상들만을 나타내었다.
첫 번째와 두 번째 모드형상은 Fig. 2의 두 번째와 세 번째인 강체 굽힘 모드의 고주파 진동으로 빔 거동의 가로-전단(transverse-shear) 변형에 해당하고 1st 면외 방향 횡진동을 나타낸다. 다음으로 세 번째 모드형상은 Fig. 2의 첫 번째인 강체 인장 모드의 고주파 진동으로 면내 방향 인장-비틀림 뒤틀림(distortion)변형을 나타내고, 1st 면내 방향 종진동을 의미한다. 이어서 네 번째, 다섯 번째 모드형상은 첫 번째와 두 번째 모드의 고주파 진동으로 2nd 면내 방향 횡진동에 해당한다. 마지막으로 여섯 번째 모드는 Fig. 2의 네 번째인 강체의 비틀림 모드의 고주파 모드형상으로 2nd 면외 방향 종진동을 나타낸다.
그리고 DVABS를 통해 구해진 Fig. 2와 Fig. 3의 결과들은 기존의 문헌7)과 비교하여 결과들의동일함으로 본 이론의 정확성을 검증하였다.
3.2 고전 빔 모델과 티모센코 빔 모델
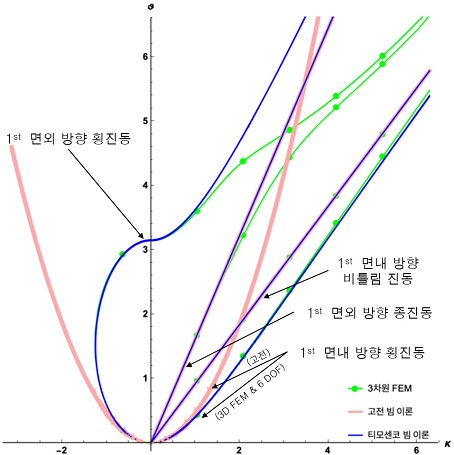
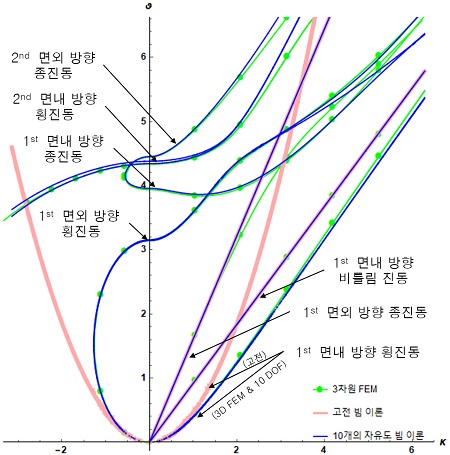
본 이론을 통한 빔모델 개발의 체계성과 확장성을 검증하기 위해, 먼저 DVABS를 통해 4개의 자유도 고전 빔모델(분홍색 실선)과 6개의 자유도 티모센코 빔모델(파란색 실선)을 구현하여 Fig. 4에 가시화하였다. 또한 본 이론의 효율성과 정확성을 검증하기 위해, 상응하는 3차원 분산곡선(연두색 원형 실선)은 상용수치해석프로그램인 COMSOLTM을 통해 구현하여 함께 나타내었다. 본 그림에서 먼저 고전 빔 모델과 3차원 FEM의 분산곡선들을 비교해 살펴보면, 차단 주파수(cut-off frequency)근처 매우 제한된 장파장 저주파 영역 외에는 고전 빔 모델을 사용한 해석결과는 다소 만족할만한 정확성을 얻기가 힘들다는 것을 확인할 수 있다.
다음은 동적 빔 거동의 해석능력을 향상시키기 위해, 고전 빔 이론의 진동 모드에 가로-전단변형인 1st 면외 방향 횡진동 모드를 추가한 6개의 자유도 티모센코 빔 모델에 대해 살펴보자. 특히 추가한 진동 모드에 의해 강체의 굽힘 변형을 나타내는 1st 면내 방향 횡진동 분기의 곡선이 고전 빔 모델의 분산곡선과 비교해 크게 향상됨을 볼 수 있다. 이러한 경향의 물리적 이유는 앞서 언급하듯이 추가한 모드형상이 강체의 굽힘 모드의 고주파 진동 모드형상이기 때문이다. 이에 따른 모드형상간의 연관성에 의해 티모센코 빔 모델이 고전 빔 모델보다 높은 정확도를 보여주지만, 빔의 동적거동을 정확히 묘사하기에는 다소 부족함을 그래프를 통해 검증된다.
3.3 최적화된 10개의 자유도 빔 모델
마지막으로, 본 연구는 티모센코 빔 모델의 정확성을 향상하기 위해 다수의 진동모드들을 추가한 빔 모델들을 개발해 보았다. 이 과정에서 각 진동모드들 간의 연관성이 존재하고, 이들의 상호작용은 분산곡선을 통해 나타나는 것을 확인할 수 있었다. 또한 단순히 많은 진동모드들을 사용하는 것이 효율적이지 않음을 확인하였고, 이러한 결과9)를 바탕으로 최소한의 진동모드 선택을 통한 최적화된 빔 모델을 소개하고자 한다.
DVABS를 사용하여 6개인 자유도 티모센코 빔 모델이후 Fig. 3에 소개된 나머지 진동모드들 4개(1st 면내 방향 종진동, 2nd 면내 방향 횡진동와 2nd 면외 방향 종진동)를 체계적으로 추가하여 빔 모델의 분산곡선을 계산하였고, Fig. 5에서 파란색 실선으로 가시화하였다.
본 그래프에서 최적화된 빔 모델의 분산곡선은 차단 주파수 근처 장파장 저주파 영역뿐만 아니라 모든 영역에서 3차원 FEM의 결과와 비교해 높은 정확성을 확인할 수 있었다. 이는 가로-전단 변형을 나타내는 진동분기(1st 면외 방향 횡진동)가 이 모드형상의 다음 순번에 해당하는 고주파 진동분기(2nd 면내 방향 횡진동)이 추가됨으로서 발생되어지는 모드형상 간의 상호작용에 의해 보정되고, 2nd 면외 방향 종진동분기가 추가됨에 따른 상호작용에 의해 1st 면내 방향 종진동분기의 보정에 의한 결과이다. 따라서 최적화된 10개 자유도 빔 모델은 장파장 영역뿐만 아니라 단파장의 영역까지 광범위한 진동영역에서 빔의 동적 거동을 효율적이고 정확한 해석할 수 있는 빔 해석모델이라고 할 수 있다.
4. 결 론
제한적 해석범위를 가진 기존의 빔 이론들과 달리, 본 연구는 동적 변분-점근법을 사용하여 광범위한 주파수 영역 내 빔의 동적거동을 분석할 수 있는 새로운 이론을 소개하였다. 먼저 차원-감소 과정을 통해 3차원 문제는 1차원 빔 문제와 2차원 단면적 문제로 나누었고 기존의 연구들과 다른 시간척도들을 사용하여 변분-점근법으로 저주파와 고주파 근사과정을 수행하였다. 또한 근사과정에서 발생되어질 수 있는 에너지의 양한정성 문제를 해결하기 위해 단파 외삽법을 도입하였다. 이 모든 과정이 DVABS로 전산화되었다.
기존의 이론들8)이 개발 편의성을 위해 사용한 이론적 가정(plane-strain, axis-symmetry 등)이 본 연구에서 사용되지 않았기 때문에, 동역학적 해석 결과를 통합적으로 나타내는 3차원 분산곡선으로 구현할 수 있었다. 이러한 통합된 분산곡선을 분석함으로서 모드형상간의 복잡한 상관관계를 파악하게 되었고, 이를 바탕으로 빔 이론 내 새롭게 추가되는 내부자유도의 역학적 영향을 논리적으로 설명할 수 있게 되었다. 또한 3차원 FEM의 3차원 분산곡선과 서로 비교함으로써 본 이론의 높은 효율성과 정확도가 검증하였다. 추가적으로, 이러한 분산곡선을 활용함에 따라 Lee5,6)가 제시한 이론 개발 방향성에 대해 간접적으로 검증하였다.
마지막으로, 본 이론으로부터 기존의 고전 이론과 티모센코 빔 이론을 구현함으로써 본 이론의 개발 신뢰도를 검증하였다. 또한 본 이론의 개발 확장성을 보여주기 위해, 티모센코 빔 이론보다 향상된 ‘개선된 빔 모델’로서 단면적 변형을 나타내는 모드형상들의 상관관계를 고려한 최적화된 10개 자유도 빔 모델을 처음으로 소개하였다.
References
-
S. Gopalakrishnan, 2016, "Wave Propagation in Materials and Structures", CRC Press, Boca Raton.
[https://doi.org/10.1201/9781315372099]

-
D. H. Hodges, 2006, "Nonlinear Composite Beam Theory", AIAA, Reston.
[https://doi.org/10.2514/4.866821]

- V. L. Berdichevsky, 1983, "Variational Principles of Continuum Mechanics", Nauka, Moscow.
-
W. Yu, 2012, "Variational asmyptotic beam sectional analysis – An updated version", International Journal of Engineering Science, Vol. 59, pp. 40-64.
[https://doi.org/10.1016/j.ijengsci.2012.03.006]

-
C. Y. Lee, 2009, "Dynamic Variational-Asymptotic Procedure for Laminated Composite Shells - Part I: Low-Frequency Vibration Analysis", Journal of Applied Mechanics, Vol. 76, No. 1, p. 011002.
[https://doi.org/10.1115/1.3002761]

-
C. Y. Lee, 2009, "Dynamic Variational-Asymptotic Procedure for Laminated Composite Shells - Part II: High-Frequency Vibration Analysis", Journal of Applied Mechanics, Vol. 76, No. 1, p. 011003.
[https://doi.org/10.1115/1.3002762]

- C. E. S. Cesnik, 1994, "Cross-sectional analysis of initially twisted and curved composite beams", Ph.D. thesis, Georgia Institute of Technology, Atlanta, USA.
- K. C. Le, 1999, "Vibrations of shells and Rods", Springer, Berlin.
- R. K. Yoon, 2020, "Dynamic Variational Asymptotic Procedure for Isotropic Homogeneous Beam Analysis", M.S. Thesis, Pukyong National University, Busan, Korea.
R. K. Yoon; Methodology, Coding, Validation and Writing-original draft. C. Y. Lee; Conceptualization, Supervision and Writing-review & editing.